Section 3  One-to-One Correspondences

The process of counting objects is familiar to everyone. It is easily seen that the set Q = {a,b,c,d,e} has 5 elements. In fact, 1 can be associated with a, 2 with b,... 5 with e. This counting process sets up a relation between the set P₅ = {1,2,3,4,5} and the set Q:

Comparing the accurate method of counting with the faulty methods, the following is observed:   In the listing of all truly related elements the relation that accurately counts the number of objects (in the above example, letters) involves all the numbers once and only once. Also the objects being counted are involved once and only once.

A room is full of married couples. (No multiple spouses, no gay marriages.) Between the set M of all men and the set W of all women in the room is an obvious relation (x is a man, and y is a woman):

[3.1] A relation between two sets is a one-to-one correspondence between the sets    if and only if    in the listing of all truly related elements
   (I) every element of the first set is involved once and only once;
   (II) every element of the second set is involved once and only once.

[3.1a] No one-to-one correspondence may exist between sets if one of them is empty.
No elements from the empty set can be involved to appear "once and only once."

It is customary to use a two headed arrow <-> denote one-to-one correspondences between elements:

[3.2] Let n be any positive integer. A set U has exactly n elements if and only if there is a one-to-one correspondence between the set P_n = {1,2,...,n} and U. The empty set has zero elements.

If a set consists of n objects without labels, often a single letter with subscripts from P_n is used:

For more examples and discussions of one-to-one correspondences click here.

In some discussions of one-to-one correspondences it may be more convenient to consider it s a truth set of ordered pairs.

[3.3] In the truth set of ordered pairs of a one-to-one correspondence between the sets
   (I) every element of the first set appears as first coordinate once and only once;
   (II) every element of the second set appears as second coordinate once and only once.

[3.4] The inverse (relation) of a one-to-one correspondence is also a one-to-one correspondence.

This statement implies that if x <-> y is true, then y <-> x is true. Again a different color is used to indicate that the inverse relation is probably a different relation. This fact often may be ignored.

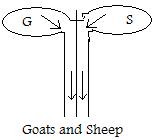One farmer inherits a large herd G of goats, and his brother, also a farmer, inherits from the same person a large herd S of sheep. The farmers want to find out if the number of animals in each herd is the same, so if the inheritance is fair. However, the uneducated farmers cannot count that high to determine the fairness. But they invent a way to do this without counting. They built two parallel shutes (passageways) and have the animals go through as pairs, one from from each herd together. (See the adjacent figure.) The process stops if either original herd becomes empty. If both become empty together, then the original herds contain the same number of animals.

Each animal goes through the chutes once and only once, and in pairs. If the hurd areas G and S are emptied that the same time, then by [3.1] a one-to-one correspondence between the sets G and S has been created.

[3.5] Two sets have the same number of elements if and only if there exists a one-to-one correspondence between them.

A more technical phrase is:   have the same cardinality.

The definition [3.2] can be rephrased as follows:    A set has exactly n elements   if and only   if it has the same number of elements as P_n. If a set has zero elements, then it is empty.

[3.6] The phrase "has the same number of elements as" is an equivalence relation between collections of sets. (Click here for a discussion of this fact.) It also provides a definition of a set being finite and an set being infinite.

[3.7] A set is finite if and only if it has exactly n elements (for some non-negative integer n).

The set P of all positive integers is a primary example of an infinite set. Any counting of all the elements of P is impossible because it never would stop. Using the ideas given above, for no positive integer n do P_n and P have the same number of elements. It is impossible to find a one-to-one correspondence between them. Recall that a proper subset does not have all the elements of the original set. If one or more elements are removed from a set of n elements to get a subset it is obvious that the subset will have fewer elements and must be proper. This can be stated as follows:

[3.8] There does NOT exist a one-to-one correspondence between a finite set and any proper subset. For a discussion that supports this statement click here.

But there are sets that do have just as many elements as in some subsets. One such set is the set P of all positive integers. Remove the integer 1 to get a proper subset Q = {2,3,4,...}. Then

Unintuitive as it may seem, it is characteristic of infinite sets that one or more elements may be removed and the resulting subset have just as many elements as the original set before any removal. Therefore, it is a philosophical question whether there exists an infinite set of distinct tangible objects anywhere.

The set P of all positive integers, the set J of all integers, and the set R of all real numbers are examples of infinite sets. It can be shown that the first two sets have the same type of infinity, but R has an infinity "bigger" than those two. The one-to-one correspondence is a vital tool for handling infinite sets.

[3.10] For more discussions about infinite sets click here.