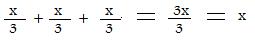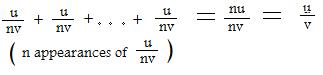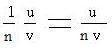Return to main page
Additional Material
To divide a given segment into equal parts
This geometrical method may use the construction of constructing a line parallel to a given line.
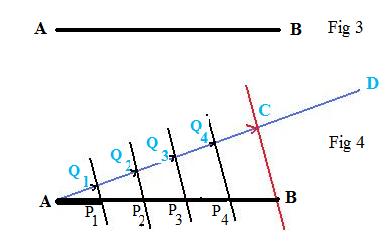 The reader may consult a book on plane geometry to see this construction. In the adjacent figure is a horizontal line segment which is to be divided into 5 parts. An auxiliary line is drawn passing through one end of the given segment. On it mark off 5 congruent segments with a compass. Pass a line through the last marked off point and the end point of the given segment. Construct lines through the 4 marked off points on the auxiliary line parallel to the line through the end point. These parallel lines will intersect the given segment at points which will separate the given segment into 5 congruent parts.
The reader may consult a book on plane geometry to see this construction. In the adjacent figure is a horizontal line segment which is to be divided into 5 parts. An auxiliary line is drawn passing through one end of the given segment. On it mark off 5 congruent segments with a compass. Pass a line through the last marked off point and the end point of the given segment. Construct lines through the 4 marked off points on the auxiliary line parallel to the line through the end point. These parallel lines will intersect the given segment at points which will separate the given segment into 5 congruent parts.
[1.1a] Geometric construction of quotients of integers
The reader may wish to recall a related geometric construction for dividing a segment into congruent parts. Click here (just above) to do this.
The number scale for integers shows markers equally spaced on a horizontal line. No mention of points between adjacent markers is made If there are any numbers corresponding to these points, those numbers cannot be "whole", i.e. integral. Numbers to correspond to some of these in-between points will be invented. Also, without losing any of its properties the system of integers will become part of this new system of numbers. (Using a technical term, the system of integers will be embedded in the new system.)
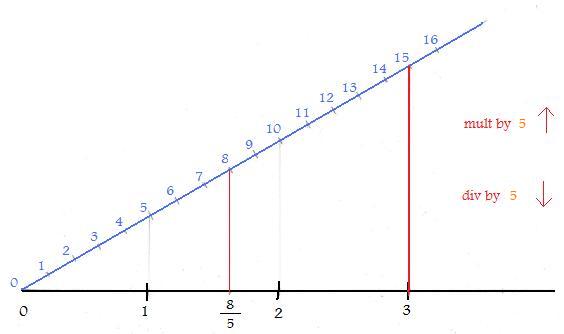 When the collection of integers were associated with points on a horizontal line the length of the intervals separating the integers was not definite, only that the separating intervals all be of the same length. The adjacent figure shows two integer number lines. On the black, horizontal line longer intervals of separation are used. On the slanted blue line the intervals of separation are much shorter. Yet on both lines all the integers are represented.
When the collection of integers were associated with points on a horizontal line the length of the intervals separating the integers was not definite, only that the separating intervals all be of the same length. The adjacent figure shows two integer number lines. On the black, horizontal line longer intervals of separation are used. On the slanted blue line the intervals of separation are much shorter. Yet on both lines all the integers are represented.
A line segment joins a number on the black line with a number on the blue line. This line segment determines a multiplying factor. In the figure 15 is joined to 3. The multiplying factor here is 15/3 = 5. By using line segments parallel to this line segment integers on the horizontal black line will be associated with integers on the blue line. For this set-up the blue integers will be 5 times the associated black integers. In the figure the association for multiplication is directed upward, from the black line to the blue line.
It is of interest to reverse the association of numbers downward. A line segment (not shown) through 10 and parallel to the red line will pass through 2. This evaluates the division of 10 by 5, to get 2. Similarly, a line segment (not shown) through 5 and parallel to the red line will join 5 with 1. This shows that the association downward forms the operation of division 5/5 = 1. The association downward (division by 5) is the opposite of the operation upward (multiplication by 5).
The association downward can be used to locate a point associated with the fraction 8/5. The line segment parallel to the line segment joining 15 and 3 will locate a point 8/5 on the black line. It is now possible to divide any integer u by 5 and locate the corresponding point u/5 on the black line, even if integer u is negative (extend both lines past zero).
By joining the natural number 1 on the black line to any non-zero number n on the blue line with a red line the multiplying and the dividing factor n is obtained by directed association, upward and downward.
[1.1a] Geometrical definition of an integer divided by a natural number To divide an integer u by a natural number n, divide the segment from zero to the marker for u into n pieces of equal length. Then for the piece with an end point on zero, determine where its other end point is located. That end point locates a point (and a marker) that will corresponds to the fraction u/n. That fraction is also called the quotient of u over n.
The number u is called the numerator of the fraction, and n is the denominator. If the numerator is 1 then the piece of length 1/n is a fractional part of the unit interval (the line segment that joins zero and one). 1/n is called the reciprocal of the natural number n.
If the segment 0~4 from 0 to the natural number 4 is divided into one piece, 4/1, it is obvious that the result is the original segment from 0 to 4. In general, u/1 = u for any integer u.
The numerator may be a negative integer. For example, the segment from zero to -3 lies to the left of zero. If it is divided into 2 parts, then one piece is a segment from zero to the midpoint of the interval [-2,-1]. The fraction is -3/2.
Many more results from the geometrical interpretation of fractions could be discussed. But it is more efficient to get results from the algebraic definition. Click here to return to the main page where the algebraic definition [1.1b] is located.
Multiplication of the reciprocal of a non-zero integer and a fraction
If a segment of length x is divided into 3 congruent parts, then each part will have a length x/3. The sum of all those parts must give the total x:
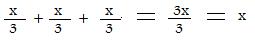 This sum shows that x/3 is the length of one part.
This sum shows that x/3 is the length of one part.
The following similar sum shows that the fraction u/(nv) is the length of one of the n parts after the fraction u/v is divided into n parts:
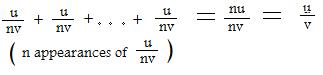 Therefore
Therefore
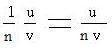 The natural number can be replaced by negative integers and the equation still holds true.
The natural number can be replaced by negative integers and the equation still holds true.

Decimal representation of rational numbers
The discussion here focuses upon fractions and zero. The corresponding discussion for negative rational numbers is easily derived from the following discussion. The discussion consists of examples, not algebraic computations.
Digits are the numbers 0,1,2,3,4,5,6,7,8,9. The notation 5382 really means 5x1000 + 3x100 + 8x10 + 2 which is equal to (5)103 + (3)102 + (8)101 + (2)100.
In a similar way, 0.5382 = 5/10 + 3/100 + 8/1000 + 2/10000 = (5)/101 + (3)/102 + (8)/103 + (2)/104.
These observations provide a discussion, not given here, that supports the following rules:
(a) If i is any positive integer, then multiplication of any real number by 10i moves the decimal point to the right i places.
(b) 10° = 1. Therefore, multiplication (or dividion) by 10° does not move the decimal point.
(c) If i is any positive integer, then division of any real number by 10i moves the decimal point to the left i places.
(d) If j is any negative integer, then multiplication of any real number by 10j moves the decimal point to the left |j| places.
Examples for part (a): 3.45678 x 103 = 3456.78; 0.00012345x102 = 0.012345
Examples for part (c): 76543.0 / 104 = 7.6543; 3.45678 / 103 = 0.00345678
Examples for part (d): 76543.0 x 10--4 = 7.6543; 3.45678 x 10--3 = 0.00345678
Obviously, parts (c) and (d) are equivalent.
Consider now the most simple situation of repeating blocks of digits in a decimal representation:
x = 0.436436436436436...
Obviously the block is 436. This can be "isolated" as a natural number in front of the decimal point by multiplying x by 103.
103x = 436.436436436436......
Now subtract x to get
103x -- x = 436
Solving for x: x = 436/(103 -- 1) = 436/999.
This is a rational number.
So is 0.1234123412341234... = 1234/9999.
In the situation y = .00234234234234... the repeating blocks do not occur just after the decimal point. Then use 102y = .234234234234... = 234/999. Then y = 234/99900
If z = 837.456456456456456... , then z -- 837 = .456456456456456456... = 456/999. Then z = 837 + 456/999 = 836619/999.
In some cases the decimal expansion is finite: .125 = 125/103 = 1/8.
With a decimal with repeating blocks it is possible to derive an equivalent fraction containing 999...9 in the denominator. If the decimal is finite, then it is possible to derive an equivalent fraction containing 100...0 in the denominator.
-------
Given a fraction it is possible to get a decimal expansion, by dividing the denominator into the numerator. The decimal expansions of some fractions are finite. For example, 1/16 = 0.0625, 1/125 = 0.008, 1/(16x125) = 1/2000 = 0.0005 . Because 2 and 5 are factors of 10 then
for any non-negative integers p,q, 1/(2p5q) always produces a finite decimal.
Next the most simple situation: fraction m/n where m is less than n, and also m and n are relatively prime natural numbers (they are in lowest terms, no common factors). The following is repeated use of the divisional algorithm of natural numbers and is partially equivalent to dividing the denominator n into the numerator m .
10m = n q1 + r1, r1 < n
102m = n q2 + r2, r1 < n
. . . . . . . . . . . . . . .
10im = n qi + ri, r1 < n
. . . . . . . . . . . . . . .
10nm = n qn + rn, rn < n
All the partial quotients q1, q1, . . . ., q1, . . . ., q1, and all the remainders r1, r2, . . . . . ri, . . . . . . rn are non-negative integers. Moreover, all the remainders r1, r2, . . . . . ri, . . . . . . rn are less than n itself.
But if any of these remainders are zero, say ri = 0, then 10im = n qi. Then m/n = qi/10i which is a finite decimal.
Suppose now that none of the remainders r1, r2, . . . . . ri, . . . . . . rn are zero. Then all of them are natural numbers less than n. But there are at most n--1 distinct natural numbers less than n. So at least two of the remainders are equal, say ri = rj where i < j. This means that 10jm = n qj = 10im = n qi. By simple algebra, m/n = (qj -- qi) / (10j--i -- 1) . This is a non-negative integer qj -- qi divided by a natural number comprised of 9's 10j--i -- 1 which creates a decimal expansion with adjacent repeating blocks all equal to qj -- qi.
If m/n is equal to or larger than 1, then find the largest non-negative integer less than or equal to m/n, and subtract it. After getting the decimal expansion for the reduced fraction, add the non-negative integer to it.
 When the collection of integers were associated with points on a horizontal line the length of the intervals separating the integers was not definite, only that the separating intervals all be of the same length. The adjacent figure shows two integer number lines. On the black, horizontal line longer intervals of separation are used. On the slanted blue line the intervals of separation are much shorter. Yet on both lines all the integers are represented.
When the collection of integers were associated with points on a horizontal line the length of the intervals separating the integers was not definite, only that the separating intervals all be of the same length. The adjacent figure shows two integer number lines. On the black, horizontal line longer intervals of separation are used. On the slanted blue line the intervals of separation are much shorter. Yet on both lines all the integers are represented.
 The reader may consult a book on plane geometry to see this construction. In the adjacent figure is a horizontal line segment which is to be divided into 5 parts. An auxiliary line is drawn passing through one end of the given segment. On it mark off 5 congruent segments with a compass. Pass a line through the last marked off point and the end point of the given segment. Construct lines through the 4 marked off points on the auxiliary line parallel to the line through the end point. These parallel lines will intersect the given segment at points which will separate the given segment into 5 congruent parts.
The reader may consult a book on plane geometry to see this construction. In the adjacent figure is a horizontal line segment which is to be divided into 5 parts. An auxiliary line is drawn passing through one end of the given segment. On it mark off 5 congruent segments with a compass. Pass a line through the last marked off point and the end point of the given segment. Construct lines through the 4 marked off points on the auxiliary line parallel to the line through the end point. These parallel lines will intersect the given segment at points which will separate the given segment into 5 congruent parts.