Return to main page
Additional Material for Chapter 3
Addition of signed integers
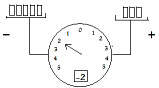 To the right is a figure of a "super" platform balance. Weights are loaded onto the two platforms. Onto the left platform 5 (pounds, kilograms,..) are loaded, onto the right platform 3. On one scale an arrow points to the side of the heaver weight (in this case to the left) . The scale also indicates how much heavier the heavier platform is (in this case 2). The arrow scale gives these two pieces of information.
To the right is a figure of a "super" platform balance. Weights are loaded onto the two platforms. Onto the left platform 5 (pounds, kilograms,..) are loaded, onto the right platform 3. On one scale an arrow points to the side of the heaver weight (in this case to the left) . The scale also indicates how much heavier the heavier platform is (in this case 2). The arrow scale gives these two pieces of information.
There is another measuring indicator showing numbers in a rectangular window. It also indicates the excess weight (in this case 2). But to indicate which side, a minus sign is attached. A minus sign indicates the left platform, a plus sign indicates the right platform. The integer -2 gives both pieces of information, which platform is heavier and by how much..
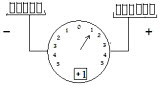 The figure to the right shows the same machine but 6 weights are in the right platform and 5 are in the left platform. This time the heaver weight is on the right (+) platform. The weight there is 1 heaver than the weight on the left platform. The arrow scale leans to the right and points to 1. The numeric scale shows a +1.
The figure to the right shows the same machine but 6 weights are in the right platform and 5 are in the left platform. This time the heaver weight is on the right (+) platform. The weight there is 1 heaver than the weight on the left platform. The arrow scale leans to the right and points to 1. The numeric scale shows a +1.
By placing all the weights on one platform and no weights on the other platform the machine converts natural numbers (the weights themselves) into signed integers (as seen in the rectangular window on the scale). After locating a point O (the origin) the integers locate points indicated by vertical markers on the line as shown in the figure to the right. The weights themselves determine how far a marker is from the origin. The integer +4 is the weight 4 on the platform on the right (nothing on the left platform) and 4 is the disstance between the origin and the marker. Similarly -3 is associated with a marker on the left of O. The weight there is 3 (no weights on the right platform) and he distance between the marker and O is 3. Zero 0 and the origin O coincide.
The signs of integers tell onto which platform of the machine to load weights . +4 means to place a weight of 4 on the right platform. -6 means to load a weight of 6 onto the left platform. The machine shows the sum of these in the rectangular window. It will be -2.
The machine gives a physical method for the addition of integers.
To find the sum of +2 and +3, load weights of 2 and 3 onto the right platform, and load nothing onto the left platform. The sum will be +5. Similarly the sum of -2 and -3 will involve the left platform and the sum will be -5. From using the machine the following laws for addition of integers can be determined:
[1.2] (Addition of signed integers)
(a) If two (or more) integers have the same sign, then add their absolute values and take the common sign for the sum.
(b) If two integers have different signs, then subtract their absolute values with the limited subtraction for natural numbers and take the sign of the integer with the larger absolute value.
Theoretically, the machine can produce the sum of any two integers.
 To the right is a figure of a "super" platform balance. Weights are loaded onto the two platforms. Onto the left platform 5 (pounds, kilograms,..) are loaded, onto the right platform 3. On one scale an arrow points to the side of the heaver weight (in this case to the left) . The scale also indicates how much heavier the heavier platform is (in this case 2). The arrow scale gives these two pieces of information.
To the right is a figure of a "super" platform balance. Weights are loaded onto the two platforms. Onto the left platform 5 (pounds, kilograms,..) are loaded, onto the right platform 3. On one scale an arrow points to the side of the heaver weight (in this case to the left) . The scale also indicates how much heavier the heavier platform is (in this case 2). The arrow scale gives these two pieces of information.
 The figure to the right shows the same machine but 6 weights are in the right platform and 5 are in the left platform. This time the heaver weight is on the right (+) platform. The weight there is 1 heaver than the weight on the left platform. The arrow scale leans to the right and points to 1. The numeric scale shows a +1.
The figure to the right shows the same machine but 6 weights are in the right platform and 5 are in the left platform. This time the heaver weight is on the right (+) platform. The weight there is 1 heaver than the weight on the left platform. The arrow scale leans to the right and points to 1. The numeric scale shows a +1.