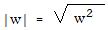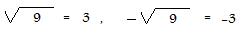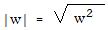A perfect square is an integer that is equal to a product of some integer with itself. Often the word "perfect" is omitted. According to [3.10a,b,e] a perfect square is never negative. (Therefore, a perfect square is equal to its own absolute value.) There are two ways that a positive perfect square can be formed: (1) a product of two equal positive integers, or (2) a product of two equal negative integers. Each of those are square roots of the perfect square. For example, since 9 = 3x3 and 9 = (-3)x(-3) then both 3 and -3 are square roots of 9. The familiar symbols
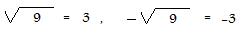
indicate this. The square root symbol wiithout a sign before it means to take the positive (more exactly, the non-negative) square root. (Sometimes the symbol sqrt(n) will be used mean the square root of n for any nonnegative integer n. The reader may replace the sqrt symbol by the more familiar square root symbol.)
A useful algebraic method of producing the absolute value of an integer is the following:
Lemma (*) The absolute value of any integer is equal to the square root of the square of that integer.
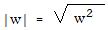
In the sqrt notation, this can be written: |w| = sqrt(w2).