Additional material
Chapter 1 Part2 : Open Statements and Quantifiers
Section 1: Basic ideas about open statements
In Chapter 1 Part A, all logical statements had truth values. In this section objects (more often their names) will receive truth values. For an intuitive introduction to this idea click here.
[1.1] Open Statements An open statement in x associates with the name of each object in a collection, called the universe of the open statement, a logical statement. Such a logical statement is called a component of the open statement. It is obtained by replacing the x (or any other variable letter) in the open statement with the name or symbol of the object. In this way, the open statement "gives" a truth value to each object in its universe through all of its components.
Suppose the open statement in x is: "x is greater than 3". The universe is the collection {1,2,3,4,5} of the first five natural numbers. Replace the x by each of these numbers to get the five components (or component statements):
1 is greater than 3
component is F
1 receives an F
2 is greater than 3
component is F
2 receives an F
3 is greater than 3
component is F
3 receives an F
4 is greater than 3
component is T
4 receives an T
5 is greater than 3
component is T
5 receives an T
Numbers like 6, 7, 3/2, 0, -2, π do not receive any truth values from this open statement because they are outside the universe for this open statement. None of them are allowed to replace the x in this discussion.
Sometimes a different variable might be used in an open statement. "x is greater than 3" and "y is greater than 3" produce the same components when the universes are the same.
An open statement has no truth value. But all of its components are logical statements with truth values. It may happen that all the components have the same truth value. In a sense these are extreme situations.
[1.2a] An open statement is universally true if all of its components are true (every object in its universe receives a T).
[1.2b] An open statement is universally false if all of its components are false (every object in its universe receives an F).
In a sense, a universally false open statement is a denial of everything. For an example the equation 2x = 7 is universally false for (a universe of) all natural numbers 1,2,3,4,.... . (A solution requires a fraction.) The equation is never true for integers. In contrast the equation x + 1 = 1 + x is universally true for all integers. Universally true equations often are called identities in algebra.
For open statements with small universes it may be possible to prove universal truth or falsehood by examination of each object in the universe for a T or by examination of each object in the universe for an F. For large or infinite universes, like the integers, other methods must be used. A common method is to use implications involving open statements. This is discussed at the end of the next section. Less often assumptions are made.
Looking at [1.2a] it seems obvious that an open statement is universally true if it does not assign an F to any object. But this statement will solve a dilemma later: it may happen that the universe is empty, no objects are in it. So, an open statement cannot assign an F to any object. The following solves this dilemma:
[1.2c] An open statement with an empty universe is universally true.
It was useful for logical statements to have a notation p, q, r etc. The notation p(x), q(x), r(x) will often be used to denote open statements in x. For example,
p(x): x is greater than 3 universe = {1,2,3,4,5}
q(x): 1 + x = x + 1
universe = {1,2,3,4,5,6,7,8,9,10,11,...}
r(x): 2x = 7
universe = {1,2,3,4,5,6}.
This notation for open statements also denotes components produced by replacing the x.
p(4): 4 is greater than 3, q(4): 4 + 1 = 1 + 4, r(4): 2(4) = 7
These components have truth values:
p(4) T,
q(4) T,
r(4) F.
To simplify wording, objects and their names are often identified to be the same. If an object has the name b and that name b receives a truth value, then the object also receives that same truth value.
Usually no confusion will result from a name and its object being the same.
In algebra the numbers that are solutions to equations are more important than the numbers that do not satisfy the equation. Similarly, in a universe the objects receiving a T are often more important than objects receiving an F.
[1.3] Truth sets In the universe of an open statement the collection of (the names of) all objects receiving a T from that open statement is called the truth set of that open statement. It is sometimes called the solution set if the open statement is an algebraic equation with an unknnown and a universe of numbers.
The truth set of "x < 4" with universe {1,2,3,4,5,6,7} is {1,2,3}. Each of the numbers 4,5,6,7 produce false components. {1,2,3} is also the solution set of "x < 4".
The truth set is the whole universe if and only if the open statement is universally true. Algebraic identities like x + 5 = 5 + x are universally true and the universe is also the truth set.
It may happen that it is not correct to say that an open statement p(x) is universally true. This says that not all objects in the universe of p(x) receives a T. Some object (one or more) receives an F.
[1.4] Counterexample An open statement cannot be universally true if some object in its universe receives an F. That object is called a counterexample to the (logical) statement that the open statement is universally true.
A counterexample is really an exception. In the previous example, "x<4" is not universally true, because 5 is in the universe {1,2,3,4,5,6,7} and is a counterexample. 5 receives an F because 5<4 is false. Only one counterexample is needed. Other exceptions may exist, but are not needed.
Let the universe be all people in our world. The open statement is "x lives in the USA". This open statement is not universally true because the queen of England is a counterexample.
There can be no counterexamples if the universe is empty. Another reason for an open statement with an empty universe to be universally true. (See [1.2c].)
An open statement assigns truth values to all the objects in its universe. Usually some receive a T, the rest receive an F. The assignments by "x < 4" to numbers in the the universe {1,2,3,4,5,6,7} in the last example are:
1 T, 2 T, 3 T, 4 F, 5 F, 6 F, 7 F.
The open statement "x + 1 < 5" obviously makes the same assignments. It is logically equivalent.
[1.5] Equivalence of open statements Two open statements p(x) and q(x) are logically equivalent if and only if they have the same universe and they assign the same truth values to each object in the universe. If a is any object in the universe, then p(a) and q(a) have the same truth value.
Notation p(x) <==> q(x).
Where as equivalent open statements assign the same truth values, it may happen that a second open statement assigns opposite truth values. For example, the open statement "x > 3" makes different assignments:
1 F, 2 F, 3 F, 4,T, 5 T, 6 T, 7 T..
The pattern is obvious, the open statements "x < 4" and "x > 3" assign opposite truth values to each number in the common universe {1,2,3,4,5,6,7}. In a sense the two open statements completely "negate" each other.
[1.6] Negatives of open statements A logical negative or logical denial ~p(x) of an open statement p(x) is another open statement that has the same universe but assigns the opposite truth value to each object in that universe.
In the previous example, if p(x): x < 4, then ~p(x): x is not less than 4.
Each of the components are negated. This is the way that each object receives the opposite truth value.
English provides a grammatical method of negation, involving words like not. If p(x): x is less than 4, then ~p(x): x is not less than 4. Another recommended method of denial is: ~p(x): it is false that x is less than 4.
Switching the direction of an inequality sign does not form a (complete) negative of an open statement. "x>4" is not the logical negative of "x<4", because both open statements assign the same truth value (F) to 4. Logical negatives must assign opposite truth values to every object in the universe.
It has been said that logic here is interested only in truth values. For that reason the open statement q(x): x>3 is also the negative of p(x). The reader can easily verify that q(x) assigns the opposite truth value to each number in the universe {1,2,3,4,5,6,7} that p(x): x<4 assigns. It may be said that q(x) is equivalent to the negative of p(x): q(x) <==> ~p(x). As far as logic is concerned, q(x) is just another form of the negative of p(x).
Again let the universe be {1,2,3,4,5,6,7}. The open statement x = 3 is not the negative of the open statement x = 6. Yet they both cannot be true for any number in the universe. Let a new universe be all people on Earth. The open statement x is in Europe is not the negative of x is in Canada. Yet both cannot be true for any person x. These are two situations of incompatibility of open statements.
The following table shows the truth values given to each number in the universe {1,2,3,4,5,6,7} by the pair of open statements x = 3, x = 6:
replace x by x = 3 x = 6
1
F F
2
F F
3
T F
4
F F
5
F F
6
F T
7
F F
This table suggests the following definition:
[1.7] Incompatible open statements Two open statements with the same universe are incompatible if and only if each object in the universe is assigned an F from one or both of them.
(No object receives T's from both of the open statements.)
Intuitively speaking, incompatible conditions are too severe for anything to satisfy all the conditions. There is an obvious extension of incompatibility to more than two open statements.
Any open statement and its negative are incompatible, because both cannot become true for any object in its universe. Incompatibility is more general than negativism.
In algebra incompatible equations are called inconsistent. The equations x + 1 = 4 &nbap; and x + 21 = 88 are inconsistent, where the universe is the collection of all integers. No number can satisfy both equations. Many numbers satisfy neither equation.
Again the reader should be reminded that open statements themselves do not have any truth values. But they have component statements that have truth values, and which assign truth values to objects in the universe of the open statement. Open statements inherit logical equivalence, negativism and incompatibility directly from their components and from the truth values assigned to all objects in their universes.
Section 2: Logical connectives between open statements
The equivalence symbol <==>, defined in [1.5] above, is an example of a connective between two participating open statements. Incompability can be given in the form of a connective: "is incompatible with".
Discussed below in this section are the major connectives and, or, implies, is equivalent to. Intuitively speaking, the idea is to insert any of these connectives between two open statements. A requirement is that the participating open statements have the same universe. Then the expression with the connective and the two participating open statements becomes a compound open statement. It will assign truth values to every object in the universe.
Suppose attention is focused on the numbers 3,4,5 in the universe {1,2,3,4,5,6,7}. Excluded from this focus are the numbers 1, 2. The open statement x > 2 also excludes 1, 2 by assigning F's to them. An additional open statement is needed to exclude 6, 7. The open statement x < 6 does this. Both open statements are needed to exclude the numbers 1,2,6,7. It is natural to use the connective and and say x > 2 and x < 6 .
To decide what truth values this new open statement
x > 2 and x < 6
assigns numbers in the universe, look at its components. The components are logical conjunctions as discussed in part A of this Chapter 2
1 > 2 and 1 < 6
F and T = F
2 > 2 and 2 < 6
F and T = F
3 > 2 and 3 < 6
T and T = T
4 > 2 and 4 < 6
T and T = T
5 > 2 and 5 < 6
T and T = T
6 > 2 and 6 < 6
T and F = F
7 > 2 and 7 < 6
T and F = F
The first two components of the conjunction are false, and the last two components are false. Therefore, the truth set of this new (compound) open statement is {3,4,5}.
[2.1] Conjunction of two open sentences A logical conjunction of two open statements with a common universe is an open statement which assigns a T to any object in that universe if and only if both participating open statements assign a T to that object. Otherwise the logical conjunction assigns an F to an object.
Notation: p(x) and q(x) assigns a T to an object a in the common universe if and only if p(a) is T and q(a) is T.
There is a natural extention to a conjunction of several participating open statements, all with the same universe. Any object in that universe receives a T from the conjunction if and only if every participating open statement assigns a T to that object. Otherwise the object receives an F from the conjunction.
Notice that the conjunction of two incompatible open statements (with the same universe) is universally false.
Using again the universe {1,2,3,4,5,6,7} and let x < 3 and let x > 5 be open statements with that universe. The alternation x < 3 or assigns the following truth values to the objects (numbers) in the universe:
1 < 3 or 1 > 5
T or F = T
2 < 3 or 2 > 5
T or F = T
3 < 3 or 3 > 5
F or F = F
4 < 3 or 4 > 5
F or F = F
5 < 3 or 5 > 5
F or F = F
6 < 3 or 6 > 5
F or T = T
7 < 3 or 7 > 5
F or T = T
The first two components of the alternation are true, and the last two components are true. Therefore, the truth set of this new (compound) open statement is {1,2,6,7}.
[2.2] Alternation of two open sentences A logical alternation of two open statements with a common universe is an open statement which assigns an F to any object in that universe if and only if both participating open statements assign an F to that object. Otherwise the logical conjunction assigns an T to an object.
Notation: p(x) or q(x) assigns an F to an object a in the common universe if and only if p(a) is F and q(a) is F.
There is a natural extention to a alternation of several participating open statements, all with the same universe. Any object in that universe receives an F from the alternation if and only if every participating open statement assigns a F to that object. Otherwise the object receives an T from the alternation.
It is obvious that the statement
if a number is less than 3 then that number is less than 5
is true. Smaller numbers are less than bigger numbers. This can be given as an implication of open statements:
if x is less than 3 then x is less than 5
This implication is universally true. For no number replacing x is the hypothesis T and the conclusion F.
Consider now the trivial inequalities (open statements) x > 5, x > 3 . Let the universe be again {1,2,3,4,5,6,7}. The following table shows the truth values given to each number in the universe {1,2,3,4,5,6,7} by the pair of open statements x > 5, x > 3:
replace x by x > 5 x > 3
1
F F
2
F F
3
F F
4
F T
5
F T
6
T T
7
T T
There are many Fs and some Ts. But in any row there is no T under x > 5 and at the same time no F under x > 3. This suggests the following definition:
[2.3] Implication of open statements One open statement implies a second open statement if nothing in the universe receives a T from the first open statement (hypothesis) and at the same time an F from the second open statement (conclusion).
Notation: p(x) ==> q(x) where participating open statements p(x), q(x) have the same universe.
[2.4] Counterexample Should an object a in the universe receive a T from p(x) (component p(a) is T) and at the same time, an F from q(x) (component q(a) is F) then the implication p(x) ==> q(x) is false. Such an object a is called a counterexample to the implication.
Consider the implication x is outside Canada ==> x is in Europe where the universe is the collection of all people in the world. Obviously it is possible to be outside Canada, yet not be in Europe. For example, the president of the USA (when he is in Washington DC). Therefore the president is a counterexample to the implication, and proves the implication false. The counterexample shows that the implication is not universally true.
With the universe of all integers (positive, negative, zero) the implication x2 = 9 ==> x = 3 is not universally true. -3 is a counterexample.
Often it is necessary to prove that an open statement q(x) is universally true. The universe is too large to examine all objects in it for truth values. Instead it is possible to find a universally true open statement p(x) with the same universe. Then it is possible to prove the implication p(x) ==> q(x) through a chain of true implications p(x) => r1(x), r1(x) => r2(x), ..., rn(x) => q(x). This method is called a direct proof of q(x).
Discussions in Part A of Chapter 2 about pairs of logical statements extend to open statements through component logical statements. Implications of open statements have converses and contrapositives defined similarly to the converses and contrapositives of logical statements.
[2.5] Equivalence Two open statements with the same universe imply each other if and only if they are equivalent.
Section 3: Quantifiers
As was stated in the previous section, an open statement p(x) has no truth value by itself. But it does have a universe, and each object or element in that universe receives a T or an F from the open statement. A question here may be, how many of the elements in the universe receive a T? Less often is the question, how many receive an F?
In some situations the open statement p(x) is universally true. This means that all components are true, that a T is assigned to every object or element in the universe.
For example,
for every integer x, x + 1 = 1 + x
for every integer x, it is false that x2 = -1
Both of these statements are true. But the following is obviously false:
for every integer x, x2 = 9
because the squares of many integers are not equal to 9.
[3.1] Universal quantifiers A universal quantifier says that an open statement assigns the same truth value to every object in the universe.
The universal quantifier that expresses the assignment of a T to every object in the universe may be expresed in any of the following forms:
for every x, p(x)
for each x, p(x)
for all x, p(x)
for any x, p(x)
Sometimes the universe is indicated before the variable in the quantifying phrase:
for all integers x, x + 1 = 1 + x
for any triangle x, x has three sides
The universal quantifier that expresses the assignment of an F to every object in the universe may be expressed as follows:
for no x
not for any x
Specific examples:
for no triangle x, x has 4 sides
for no integer x, x2 = -1
Actually this negative existential quantifier is not needed. The open statements may be restated with the negative part moved to the open statement itself and the positive universal quantifier is used:
for all triangles x, x does not have 4 sides
for all integers x, x2 is not equal to -1
for no x, p(x) is equivalent to for all x, ~p(x)
Intuitively speaking, the universal quantifier makes a "sweeping" statement about the whole universe. The quantifier in the next definition "looks more carefully".
[3.2] Existential quantifier An existential quantifier says that there exissts at least one object in the universe to which the open statement assigns a T.
In these discussions the first letters of the alphabet a, b, c, ... are symbols that can be replaced by the name of a single object. They act like constants in these discussions. However the last letters ..., x, y, z are often variables that can be replaced by (the name of) any object in the universe. The reader, of course, is free to use any letters, ignoring the differences between variables and constants. Their distinction is not of major importance. The letter a may be in boldface (dark black) to distinguish it from the English indefinite article a.
The existential quantifier may be expressed as follows:
there exists an a, p(a)
there exists an a such that p(a) (a more grammatical expression in English)
for some a, p(a)
The following are true statements:
There exists an integer a such that a2 = 9
There exists a triangle b such that b has a right angle
For some city c, c has more than a million people in it.
For some integer d, d + 1 = 1 + d
The word exists is an essential part of an existential quantifier. This means that the universe cannot be empty. There must be one or more objects in it so that some object is assigned a T. It is quite possible that the open statement assign T's to several or many objects, perhaps all objects in the universe. The number of objects receiving T's is not important, as long as the number is not zero. Notice, however that the existential quantifier does not give the (name of the) object receiving a T. It merely makes the statement that the object exists.
[3.3] Existential quantifier with an empty universe If p(x) is an open statement with an empty universe, then the following statement is false:
there exists an object a such that p(a)
Sometimes it is desirable to indicate that there exists exactly one object receiving a T from an open statement. For example, 2x + 6 = 20 can be solved and anyone familiar with elementary algebra knows that there is a single number that will satisfies this equation. That number is unique. This uniqueness is expressed in the quantifying phrase:
there exists a unique integer a such that 2a + 6 = 20
Similarly, there can be only one president of the USA.
there exists a unique person a such that a is president of the USA
In other words the open statement assigns only one T. All other assignments are F.
[3.4] Uniqueness quantifier The following expression is true if and only if there is exactly a single object a in the universe of the open statement p(x):
there exists a unique object a such that p(a)
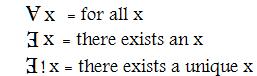 In works of mathematics and logic there are two symbols often used in these quantifier expressions They are shown in the figure at the right: an upside-down A and a backwards E. They are not used in these discussions. Instead, the quantifying phrases will be given in English.
In works of mathematics and logic there are two symbols often used in these quantifier expressions They are shown in the figure at the right: an upside-down A and a backwards E. They are not used in these discussions. Instead, the quantifying phrases will be given in English.
[8.4]
Let p(x) be any open statement with some associated universe. If, however, that universe be empty, then the statement
(for all x) p(x)
must be true.
To support this strange statement, look again at definition [8.1]. To be false there must exist a counter-example, an a that receives an F from p(x). But there is no element in the universe to receive any truth value. The quantified statement is said to be vacuously true.
It is obvious that the following statement is true:
(for no integer x) x + 1 = x
It simply says that the open statement x + 1 = x assigns an F to every integer, and this is true. If the negative x + 1 is not equal to x is used, then this open statement assigns a T to every integer. Therefore:
(for every integer x) x + 1 is not equal to x
is true. A quantifer with "no" or "none" in it can be changed to a "for all..." quantifier if the open statement is changed to its negative. Seldom in these discussions is the "no" formal quantifier used.
There are names and various synonyms for these quantifying expressions:
universal quantifiers: (for all x), (for every x), (for each x), (for any x)
existential quantifiers: (there exists an a), (for some a)
Be careful with the quantifier "any." Negating it is not the same as negatinging the other universal quantifiers: "not any" is not equivalent to "not all." Instead "not any" is equivalent to universal denial "no..." discussed in a previous paragraph.
The major definitions about open statements can be expressed more precisely using universal quantifiers. Some examples are as follows. Let p(x), q(x) be open statements with the same universe.
open statements
quantified expression
(a) p(x) and q(x) are equivalent
(for all x) [p(x) <==> q(x)]
(b) p(x) implies q(x)
(for all x) [p(x) ==> q(x)]
(c)
q(x) is the denial of p(x)
(for all x) [q(x) <==> ~p(x)]
(d)
p(x) and q(x) are incompatible
(there exists an a) [p(a) is false or q(a) is false]
The expression "incompatible" is sometimes used in these notes. It may be said that
x = 4 and x=5
cannot both be true. Yet they are not denials of each other, because they do not always have opposite truth values. x may be replaced by 6, for example.
x = 4 is incompatible with x=5
In algebra the equations are called "inconsistent."
The wording of definition [8.1] shows how to negate a universally quantified open statement. Such a statement declares that every object in the universe receives a T from the open statement. The negative of this says that some object receives an F. (That same object receives a T from the negative of the open statement.)
[8.5a]
Let p(x) be an open statement with some universe. Then:
~(for all x) p(x) ==> (there exists an a) ~p(a)
Notice that the denial affects both the quantifying phrase and the open statement. Actually, this implication is an equivalence.
The denial of
(for all integers x) x2 = 9
is
(there exists an integer a) a2 is not equal to 9
The integer 5 confirms this last statement.
Similarly, to negate that some object in the universe receives a T is to say that all objects receive an F.
[8.5b]
Let p(x) be an open statement with some universe. Then:
~(there exists an a) p(a) ==> (for all x) ~p(x)
Notice that the denial affects both the quantifying phrase and the open statement. Actually, this implication is an equivalence.
The denial of
(there exists an integer a) a2< 0
is the expression
(for all integers x) x2 is greater than or equal to 0
The fact that, the square of any integer is never negative, justifies the denial. Again notice that the denial affects both the quantifying phrase and the open statement.
The quantified statements in [8.5a] and [8.5b] are contrapositives of each other.
[8.5c]
To get the denial of a quantified statement, change the quantifying phrase and negate the open statement:
expression
its denial
(for all x) p(x)
(there exists an a) ~p(a)
(there exists an a) p(a)
(for all x) ~p(x)
The commutative law for numbers says that the addition of any two numbers can be done in either order. An open statement in two variables can be made from this:
p(x,y): x + y = y + x
This is called an identity, and sometimes three dashes replace the equal sign. Two quantifying phrases will be needed to translate the identity into logical symbols:
(for all x)(for all y) p(x,y)
This is true because no pair of numbers a and b exist to make p(a,b) false. There is no pair of numbers b and a to make p(b,a) false. Therefore
(for all x)(for all y) p(x,y) <==> (for all y)(for all x) p(x,y)
The order of the two universal quantifiers is not important.
Suppose the universe is the collection of the following integers: 1,2,3,4,5, and the open statement is:
p(x,y): x2 + y2 = 25
By testing 25 possibilities:
p(1,1) = 25, p(1,2) = 25, p(1,...)
p(2,1) = 25, p(2,2) = 25, p(2,...)
it is found that only p(3,4) = 25 and p(4,3) = 25 are true statements. Since there are integers a and b that make p(a,b) false, the universal quantifiers cannot be used here. But the following is true:
(there exists an a)(there exists a b) p(a,b) is true
Again it does not matter which quantifying phrase comes first.
In elementary algebra to plot the equation x + y = 10 of a line, a partial table of values that are real numbers could be made:
x y
1 9
2 8
3 7
4 6
etc
Consider the equation as an open statement p(x,y) in two variables:
p(x,y): x + y = 10
For each value of x, a value of y can be found. This can be translated into:
(for all x)(there exists a y) p(x,y)
Of course, as different values of x are chosen, different values of y must be taken in order to satisfy the equation. In fact, y = 10 - x shows how to choose a value for y after a each value for x has been chosen.
Consider the equation:
p(x,y): x + y = x
The statement:
(for each real numbers x)(there exists a real number y) p(x,y)
is true. But the same value for y must be chosen to make it true, namely 0. The following statement is also true:
(there exists a real number a)(for all real numbers x) p(x,a)
Since the quantifying expression containing a comes first, the same value for a must work for all values of x. The statement:
(for all real numbers x) p(x,0)
is true for this situation.
Let p(x,y) be an open statement in two variables. Let a be a fixed value that does not change.
if (for all x) p(x,a) is true
then (there exists a) (for all x) p(x,a) is true
The choice for value a for y to make the open statement p(x,a) become true, does not depend upon the choice of x. y has no dependence upon x.
Click on Double Quantifiers for visual examples and discussions.
The following table shows how to negate doubly quantified expressions:
expression
its negation
(for all x)(for all y) p(x,y)
(there exists an a)(there exists a b) ~p(a,b)
(for all x)(there exists a y) p(x,y)
(there exists an a)(for all y) ~p(x,y)
(there exists an a)(for all y) p(x,y)
(for all x)(there exists a y) ~p(x,y)
(there exists an a)(there exists a b) p(x,y)
(for all x)(for all y) ~p(x,y)
The rule [8.5c] for expressions containing one quantified phrase may be extended to doubly quantified expressions: to get the negation of a quantified statement, change each quantifying phrase and negate the open statement.
Section 9 Math Induction
In 2n it is natural to think of the exponent n as a positive integer, although it is possible to discuss expressions like 2x with real numbers x as exponents. In this section the open statements will use variables that take values from the set {1,2,3,...} of positive integers. This is indicated by the use of n as variable in the symbol p(n) for an open statement.
The first n positive integers are 1,2,...,n. The sum of the first n positive integers is 1 + 2 + ... + n. There is a formula for this sum:
p(n): The sum of the first n positive integers = n(n+1)/2
There are various ways to derive this formula. (One derivation is to write the sum forward and backward and add the corresponding n terms individually to get n + 1 each time.)
An attempt to verify the formula is to check the truth value for each integer:
p(1) is true, because the sum of the first positive integer = 1 and 1(1+1)/2 = 1.
p(2) is true, because the sum of the first 2 positive integers = 3 and 2(2+1)/2 = 3.
....
p(1000) is true, because
the sum of the first 1000 positive integers = 500500 (done by an addiing machine)
and 1000(1000+1)/2 = 500500.
----
It is physically impossible to verify all of the infinitely many components p(1), p(2),.... But all is not lost. Suppose p(1) has been verified as true. Somehow prove the implication p(1) => p(2). Then prove the implication p(2) => p(3). A chain reaction has been started: p(1) => p(2), p(2) => p(3), &nsp; p(3) => p(4) , ... And the proofs of all of the implications are very similar, just a change of numbers. Instead of proving each implication, prove the general implication p(n) =>p(n+1) where n represents any positive integer.
This discussion is interrupted to state these conditions again:
[9.1] (Mathematical induction)
An open statement p(n) is universally true (true for all positive integers n) if
[a] p(1) is shown to be true and
[b] p(n) implies p(n+1).
Continuation of the discussion. Part [a] has been done . For part [b] the implication p(n) => p(n+1) must be proven
p(n+1): sum of the first n+1 positive integers =
sum of the first n positive integers + n+1 == n(n+1)/2 + n+1 = (n+1)(n+1 + 1)/2
This proves the implication. The red double or long equal sign == shows where the hypothesis p(n) is needed and used. Some simple algebra is needed to justify the last equal sign =.
Here is another example and without interruption. Let x,y be any numbers. For every positive integer n
q(n): (xy)n = xnyn
is true.
Using induction there are two parts to be proven: [a] q(1) is true, and [b] q(n) implies q(n+1).
Part [a] is trivial: q(1): (xy)1 = xy = x1y1.
Part [b] q(n+1): (xy)n+1 =
(xy)n(xy)1 = (xy)n(xy) ==
xnynxy = xn+1yn+1.
The red double or long equal sign == shows where the hypothesis q(n) is needed.
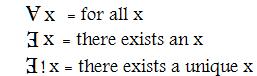 In works of mathematics and logic there are two symbols often used in these quantifier expressions They are shown in the figure at the right: an upside-down A and a backwards E. They are not used in these discussions. Instead, the quantifying phrases will be given in English.
In works of mathematics and logic there are two symbols often used in these quantifier expressions They are shown in the figure at the right: an upside-down A and a backwards E. They are not used in these discussions. Instead, the quantifying phrases will be given in English.