Trees have been discussed briefly in Chapter 2. More details are developed in this chapter.
A tree is a special kind of graph. A tree may have edges or arcs. Therefore
a tree can be either a special digraph (a directed tree) or a special ugraph (an undirected tree).
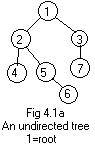
Definition of an undirected tree: a connected ugraph without any loops.
In graph theory this is the most common definition of tree.
Any node can serve as a root. In a drawing the root is the top node.
All edges slant downward. See Fig 4.1a
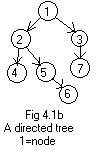Definition of a directed tree: with the exception of a one node (the root), every node is the head of a single arc (for each node except the root there is a single arrow pointing to that node).
This is a more usefull but less common definition of a tree.
Notice in Fig 4.1b that every node has a single arrow pointing to it, except node 1.
In a drawing an undirected tree can be converted to a directed tree by drawing an arc (arrow) over each edge. The arrow points downward. In this way the directed tree in Fig 4.1b is derived from the undirected tree in Fig 4.1a.
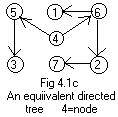In a directed tree the arrows may point in other directions, not just downward.
In Fig 4.1c the node = 4. Every node except 4 has a single arrow pointing to it.
Some general properties of trees:
Each tree has a root.
Motion can go from the root to any node in a tree.
But there is only one path for motion to go to that node.
By replacing all the arcs with the edges under them, a directed tree is converted into an undirected tree. The reverse is also possible: covering all edges of an undirected tree with downward pointing arcs produces a directed tree.
From this section 4.1 goto: additional material / problems / computer programs /
facts and theorems
===================
filler
filler
filler
From this section 4.2 goto: additional material / problems / computer programs /
facts and theorems
===================
filler
filler
filler
From this section 4.3 goto: additional material / problems / computer programs /
facts and theorems
Table of Contents /
Preface