GRAPHS
CHAPTER 2
Section 2.1 Paths, connected nodes and components
It is sometimes useful to generalize an idea. The arc (arrow) can be used to indicate motion from its tail (beginning node) to its head (ending node).
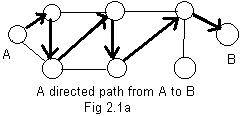 If the tail has the integer label 3, and the head the integer 5, then notation 3->5 also indicates this motion. If a second arc 5->9 has its tail 5 on the head of the first, and a third arc has its tail 9 on the head of the second, etc, a finite chain of consecutively joined arrows is constructed. At the same time an obvious chain of labels is formed: 3->5->9->6->2->8 In Fig 2.1a is such a chain that shows how motion can go from node A(=3) along the chain to node B(=8). This extends the idea of a single arc. The construction is a directed path from A to B. To traverse a path from A to B is to go from A to B along the path.
If the tail has the integer label 3, and the head the integer 5, then notation 3->5 also indicates this motion. If a second arc 5->9 has its tail 5 on the head of the first, and a third arc has its tail 9 on the head of the second, etc, a finite chain of consecutively joined arrows is constructed. At the same time an obvious chain of labels is formed: 3->5->9->6->2->8 In Fig 2.1a is such a chain that shows how motion can go from node A(=3) along the chain to node B(=8). This extends the idea of a single arc. The construction is a directed path from A to B. To traverse a path from A to B is to go from A to B along the path.
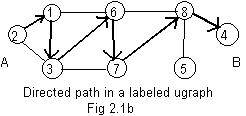 In Fig 2.1b motion can leave node C(=4), go along the chain of arcs and return to C. In that case motion completes a loop. (A loop is not considered an extension of the idea of an arc because the tail and head of an arc never coincide in our early theory of graphs.) The chain of labels for this loop in Fig 2.1b is 4->1->7->10->12->11->4
In Fig 2.1b motion can leave node C(=4), go along the chain of arcs and return to C. In that case motion completes a loop. (A loop is not considered an extension of the idea of an arc because the tail and head of an arc never coincide in our early theory of graphs.) The chain of labels for this loop in Fig 2.1b is 4->1->7->10->12->11->4
Notice that in the chain of labels for the loop in Fig 2.1b a label is repeated. A (directed) path has a loop [possibly more loops than one] if and only if some repeated integers [possibly more and different repeated integers] are in the chain of labels.
It should be remembered that these arcs or arrows are drawn over edges of some ugraph. In these two figures the ugraphs were not drawn. But there are similar statements relating a chain of edges and a chain of labels:
3-5-9-6-2-8 is an undirected path from A to B
4-1-7-10-12-11-4 is an undirected loop
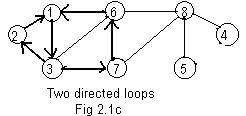 It is possible (and quite likely) a arbitrary path contain a loop. In Fig 2.1c
It is possible (and quite likely) a arbitrary path contain a loop. In Fig 2.1c
3-5-9-6-20-21-22-5-9-6-2-8
is a path from A to B with a loop. A path (directed or undirected) without any loops is called a simple path. A simple path is shorter than a path with an attached loop. Moreover a simple path avoids some problems. A loop, for example, allows perpetual motion around the loop.
To get a more general directed path, a physical situation may be helpful to explain it. Fig 2.1d shows a ugraph. It represents rooms and corridors in a large house.
 The room marked A is also the entrance to the house. A treasure is located in a distant room marked B. An obvious task is to find a way from A to B To present some ideas in graph theory in an intuitive manner two attempts to find that way will be presented.
The room marked A is also the entrance to the house. A treasure is located in a distant room marked B. An obvious task is to find a way from A to B To present some ideas in graph theory in an intuitive manner two attempts to find that way will be presented.
The first attempt is made by a small child who enters the house at room A and wanders about the house through its rooms and corridors hoping to reach some delicious candy room B. The erratic wanderings can be traced by showing the rooms he has passed through. (Assume the child always goes completely through a corridor, and not stop or turn around midway.) An unlucky child may never arrive at room B if he goes through the same rooms and corridors again and again.
An example of the path is
2->3->7->6->1->3->6->1->3->...
At the end the child is "stuck" in the loop 6->1->3->6. The basic flaw in this random wandering about the corridors and rooms is the repeated visiting of the same rooms.
The lack of effective decisions about selecting corridors make the method of random wandering undesirable. It may fail to achieve a successful arrival at a goal. (Worse yet, the child may be lost in his wanderings and never find an exit!)
A clever adult enteres the house at room A. Immediately he makes rules for movement about the house.
Rule 1: Don't visit any room twice. He keeps a list of the numbers of the rooms (including the one that he is in) that he has already visited. He will not go through a corridor to any rooms with those numbers.
Rule 2: Look for the adjacent room with the smallest number. If that number violates rule 1, then look for the adjacent room with the next smallest number. Continue looking if that number violates rule 1.
With these two rules a path can be constructed from A to B
0->2->1->3->6->7->8->4
The zero at the head of the chain is used to point to the entry node (room) 2.
The actual construction is given in the following table:
| in room | adjacent room(s) | already visited | choose next room |
|---|
| A=2 | 1,3 | 0 | 1 |
| 1 | 2,3,6 | 1,2 | 3 |
| 3 | 1,2,6,7 | 1,2,3 | 6 |
| 6 | 1,3,7,8 | 1,3,6 | 7 |
| 7 | 3,6,8 | 3,6,7 | 8 |
| 8 | 4,5,6,7 | 6,7,8 | B=4 |
It is instructive to compare the first two columns with a slightly modified adjacency array for the ugraph:
0,2, 1,2,3,6, 2,1,3, 3,1,2,6,7, 4,5,8, 5,4,8, 6,1,3,7,8, 7,3,6,8, 8,4,5,6,7, 0,0
In an intuitive sense the leading 0 denotes a "pseudo-room", an imaginary room that is just outside the entry to the house and not part of the house (an imaginary node just before the entry node 2, and not part of the ugraph).
 If the tail has the integer label 3, and the head the integer 5, then notation 3->5 also indicates this motion. If a second arc 5->9 has its tail 5 on the head of the first, and a third arc has its tail 9 on the head of the second, etc, a finite chain of consecutively joined arrows is constructed. At the same time an obvious chain of labels is formed: 3->5->9->6->2->8 In Fig 2.1a is such a chain that shows how motion can go from node A(=3) along the chain to node B(=8). This extends the idea of a single arc. The construction is a directed path from A to B. To traverse a path from A to B is to go from A to B along the path.
If the tail has the integer label 3, and the head the integer 5, then notation 3->5 also indicates this motion. If a second arc 5->9 has its tail 5 on the head of the first, and a third arc has its tail 9 on the head of the second, etc, a finite chain of consecutively joined arrows is constructed. At the same time an obvious chain of labels is formed: 3->5->9->6->2->8 In Fig 2.1a is such a chain that shows how motion can go from node A(=3) along the chain to node B(=8). This extends the idea of a single arc. The construction is a directed path from A to B. To traverse a path from A to B is to go from A to B along the path.
 In Fig 2.1b motion can leave node C(=4), go along the chain of arcs and return to C. In that case motion completes a loop. (A loop is not considered an extension of the idea of an arc because the tail and head of an arc never coincide in our early theory of graphs.) The chain of labels for this loop in Fig 2.1b is 4->1->7->10->12->11->4
In Fig 2.1b motion can leave node C(=4), go along the chain of arcs and return to C. In that case motion completes a loop. (A loop is not considered an extension of the idea of an arc because the tail and head of an arc never coincide in our early theory of graphs.) The chain of labels for this loop in Fig 2.1b is 4->1->7->10->12->11->4
 It is possible (and quite likely) a arbitrary path contain a loop. In Fig 2.1c
It is possible (and quite likely) a arbitrary path contain a loop. In Fig 2.1c The room marked A is also the entrance to the house. A treasure is located in a distant room marked B. An obvious task is to find a way from A to B To present some ideas in graph theory in an intuitive manner two attempts to find that way will be presented.
The room marked A is also the entrance to the house. A treasure is located in a distant room marked B. An obvious task is to find a way from A to B To present some ideas in graph theory in an intuitive manner two attempts to find that way will be presented.