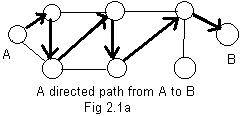The idea of motion from a node to another node in a ugraph has been introduced in Chapter 1. An arrow (arc) along the edge between those nodes represented that movement. It is very useful to extend this motion to go through several adjacent nodes to get a directed path from a node A to a node B. A ugraph with this path is shown in Fig 2.1a. A motion along this path is said to traverse the path.

Notice that in a directed path each arrow (arc) points to the tail of the next arrow, except, perhaps, for the last arrow. Obviously the indicated directed path is not the shortest path. Also, it does not pass through all the nodes, and does not traverse all the edges.

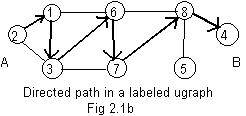There is a convenient notation for a directed path. The chain of integer labels

This path is also indicated in boldface numbers in a modified form of the adjacency array for the ugraph in Fig 2.1b:
0,2,   1,2,3,6,   2,1,3,   3,1,2,6,7,   4,5,8,   5,4,8,   6,1,3,7,8,   7,3,6,8,  8,4,5,6,7,   0,0    modified adjacency array
0->2  1->3      2->1      3->6                                  6->7          7->8        8->4     corresponding pieces of the chain.

Recall that under the arrows are edges of a ugraph. Often the arrows are removed to reveal those edges. Under a directed path is a path of edges, and that path has no direction nor motion. But two nodes are connected if there is a path from one to the other.

It is often tedious work to determine a directed path from a modified adjacency array. Fortunately a computer program can be developed without much difficulty to do that work rapidly and effectively.

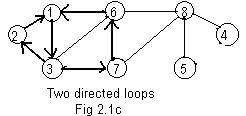A special kind of path deserves mention. It can present difficulies in some discussions about ugraphs. A loop is a (directed) path from a node back to that same node. It must involve three or more nodes. See Fig 2.1c. Using the notation of chains of integer labels, the two loops are:

A path is simple if it has no loops. The paths in Fig 2.1a and Fig 2.1b are simple. The paths indicated in Fig 2.1c are not simple paths. Using the ugraph given in Fig 2.1b the path

The graphical length of any path is the number of its edges traversed. Do not count the pointer from any zero node. The graphical length of the path in Fig 2.1a is 6.

Section 2.2 Methodical construction of paths

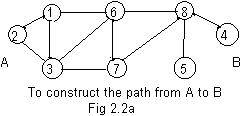Let the ugraph in Fig 2.1b represent the numbered rooms in a large house. All of the rooms are llinked by corridors as shown by edges in Fig 2.1b. The entrance to the house is at room A. A reward is placed in room B.

A young child enters the house at A, and wanders erratically through the rooms and corridors. It is quite possible that he never reaches room B. In this case the reward is some delicious candy.

The key words here are "wanders erratically." This suggests that an adult use a methodical construction ofa path. A decision must be made in each room (except B) that the adult is in.

Rule h1: Don't visit any room twice. He keeps a list of the numbers of the rooms (including the one that he is in) that he has already visited. He will not go through a corridor to any rooms with those numbers.

Rule h2: Look for the adjacent room with the smallest number. If that number violates rule h1, then look for the adjacent room with the next smallest number. Continue looking if that number violates rule 1.

With these two rules a path can be constructed from A to B

in room	adjacent rooms(s)	already visited room(s)	choose next room and go to it
A=2	1,3	0	1
1	2,3,6	1,2	3
3	1,2,6,7	1,2,3	6
6	1,3,7,8	1,3,6	7
7	3,6,8	3,6,7	8
8	4,5,6,7	6,7,8	B=4

Suppose that the treasure has been removed from room 4 and placed in room 5. The above construction will still create a directed path from A to B=4. But room 4 is a dead end. The only solution is to back up through the corridor from room 4 to room 8, even though room 8 has already been visited. An arrow indicating backing up is never drawn.. The rooms adjacent to 8 are 4,5,6,7. Of these only 5 has not been visited.

Rule h3: If a person is in a room where all adjacent rooms have been visited, then he should back up through the corridor, through which the person just came, to the previous room.

This places a person in room 8 and then the person goes down the corridor to room 5. This rule needs an exception if the room is the entrance (room 2) to the house.

Rule h4: If the person is in the room which was the entrance to the house, and all adjacent rooms have been visited, then back out of the house.

Section 2.3 Trees and components

A task in graph theory is to find (visit) all nodes connected to a given node in a ugraph. Two examples are given to show that this task has a hint of practical application in the real world.

The given node corresponds to an electrical generating plant. Then all those houses connected to that plant would have electricity generated by that plant. A check can be made to see if the distribution of electricity is complete by visiting each house. It may be more efficient to visit each house exactly once and no more.

All rooms in a house are connected somehow by corridors to the entry room then all rooms can be visited after entering the house. Suppose a detective must search each room in the house for evidence. But it requires much time while searching each room. So he does not want to search any room twice. He can use rules h1, h2, h3, h4 to do a methodical way of visiting all of the rooms.

Sometimes ugraphs are in several "pieces." Pick a start node in any piece. Then find all nodes connected with that start node. The subgraph formed from all those nodes is called a component (of the bigger ugraph) containing the start node. The component includes only those edges that are in the bigger ugraph, but which link nodes in the component. Any node not connected to that start node is in a different component.

There could be several electrical generating plants that do not share electricity. Each plant plus all the houses it serves makes a component. There could be several houses with rooms and corridors. Each house contains a component of rooms and corridors. For the benefit of future discussions the rules h1, h2, h3,h4 are rephrased for ugraphs.

Rule 1 No node will be visited more than once.

Rule 2 From any node traverse the edge to a node with the smallest integer label, that does not violate Rule 1.

Rule 3 For any reason if it is impossible to traverse an edge from a node to another, backup over the edge that led to that node. In that way arrive at a previous node. (Do not record the backup, because the motion is goes into a node that already has been visited.)

Rule 4 If it is impossible to traverse any edge from the given (starting) node then back out of that component of the ugraph and look for another component and a starting node in it.

The following rule allows a methodical way to select start nodes. (Later they will becalled roots.) The rule is part of an algorithm that becomes a computer program for finding all components of a labeled ugraph..

Rule 5 Unless indicated otherwise a start node in any component of a labeled ugraph is the unvisited node with the lowest integer label.

These rules are useful if the components cannot be seen from a drawing (drawing too complicated or no drawing at all). The adjacent nodes of each node can be given by an adjacency list or adjacency array. Usually it is very tedious for a person to traverse the ugraph in this form.