Return to main page
Additional Material
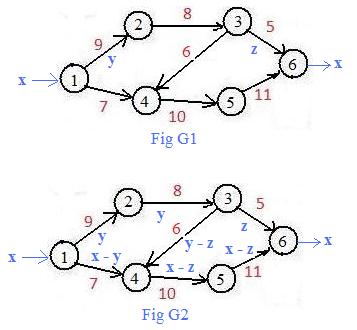
Algebraic Method for Finding Maxflow through DiGraph in Fig G
G=G1;
Let x = Maxflow. Then x enters node 1 and exits node 6.
Let y = flow through link 1→2 and let z be the flow through link 3→6. Then flow through link 1→4 must be x - y and the flow through link 5→6 must be x - z.
The flow through link 2→3 must equal the flow through link 1→2, that is y and the flow through link 4→5 must equal the flow through link 5→6, that is x - z.
The inflow y into node 3 must equal the total outflow, so the flow through link 3→4 must be y - z for this to be true. Notice then that the total inflow into node 4 does equal the outflow x - z.
The flow through link 2→3 cannot be more than the capacity of that link. Therefore,
(A) y ≤ 8
Likewise, the flow through link 1→4 cannot be more than its capacity. This means that x - y ≤ 7 which is equivalent to
(B) x ≤ y + 7
From (A) and (B) follows (C):
(C) x ≤ 15
The flow through link 3→6 cannot be more than its capacity. This means that
(D) z ≤ 5
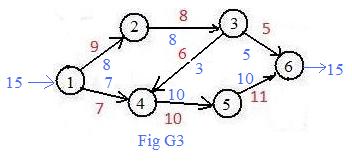Replace the weak inequalities in (A),(C) and (D) by equalities
x = 15,
y = 8,
z = 5,
Find the flow through each link by substituting these values for x,y,z in the corresponding expressions in Fig G2 to get Fig G3. The fact that
total inflow = total outflow
is true at every node, the flow through each link is not more than the capacity, together with (C) means that
x = 15
is the maximum flow through the graph.