Construction of a path in a connected graph that visits every node once and only once
More exactly traversing the graph visiting every node once and only once.
By definition the links of a Ugraph are bidirectional. However, motion along a path has a single direction. Since motion will be fundamental to this discussion, a premature use of direction along some links will be used before discussions in the next chapter about Digraphs.
The computer controls a robotic bug . It directs the bug to visit all the nodes in a connected Ugraph. There must be a first node which marks the start of the journey of the bug about the graph, and a last node when the bug has finished the task.
During the journey the bug most often enters a node from some link and goes out of that node along a different link. The task is simple for traversing all the nodes in the linear graph in Fig Z1 from left to right.
The journey is more complicated if some nodes have more than one way out (degree 3 or higher). A decision must be made in each where to exit the node. One decision: choose the exit to the left of where the bug entered. But how does the computer know in an unlabeled graph which exit is to the left so it can direct the bug to it?
In the chapter 4 the computer will use numbers assigned to all the links to be used for the choice of exits from nodes. In this discussion the numerical labels assigned to each node will be used. In the full adjacency list after each (node) is a list of all of its adjacenct neighbors. When the bug is in a node, the computer selects the neighbor with the lowest number and directs the bug to exit along the link that leads to that neighbor.
Three common problems arise and additional parts will be added to this method to solve them:
(a) while trying to visit all nodes the bug may visit some nodes more than once;
(b) by choosing every time a neighbor with the smallest label number the bug may traverse an endless loop;
(c) after moving along a path through nodes, the bug may enter a node with no other way out.
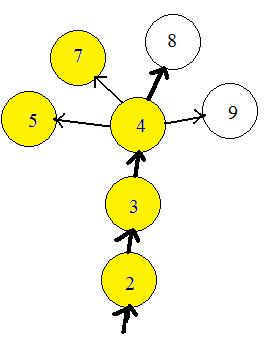The computer can prevent the bug from entering any node more than once, by remembering what nodes have been visited. It puts a mark by the label number if the node has been visited. In Fig Z2 the nodes already visited are colored yellow. The computer bug moves along through nodes 2 and 3 and enters node 4. Nodes 5 and 7 have been visited. The neighbor with the lowest number label is 8. The bug exits node 4 and goes to 8. Then node 8 will become yellow. The computer will actually put a mark by label 8.
This provides a decision in nodes with more than one exit. It is one part of a method for construction of the path.
This solves (a) and (b).