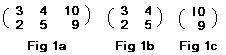
The splitting of the matrix in Fig 1a produces two matrices in Fig 1b and Fig 1c. The matrix in Fig 1b is a 2x2 matrix. It is a square matrix. It is called the coefficient matrix of the equations:
[5]
Similarly, the simultaneous equations
[3]
To handle the three situations, no solutions, one unique solution, infinitely many solutions, it is convenient to "split" the matrix of the equations into two associated submatrices.
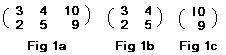
The splitting of the matrix in Fig 1a produces two matrices in Fig 1b and Fig 1c.
The matrix in Fig 1b is a 2x2 matrix. It is a square matrix. It is called the coefficient matrix of the equations:
[5]
Zeros play an important role in matrices. Consider the coefficient matrix and the right hand column matrix
6 0 0 0 0 42 0 1 0 0 0 4 0 0 7 0 0 7 0 0 0 4 0 12 0 0 0 0 2 4shows a coefficient matrix separated from the right column matrix. It is very easy to find the solutions 7, 4, 1, 3, 2.. Divide the first row (in each matrix) by 6, the third by 7, etc. The result is
1 0 0 0 0 7 0 1 0 0 0 4 0 0 1 0 0 1 0 0 0 1 0 3 0 0 0 0 1 2Both of these matrices are diagonal matrices. They have integers = 0 everywhere except on the diagonal. ( There may be zeros there also.) This is the main diagonal, from upper left to the lower right. There is another diagonal, from lower left to upper right.
The diagonal matrix [6] with all 1's on its main diagonal is called an identity matrix. Motivation for the name "identity" will be given later. The symbol I5 can be used to designate the 5x5 identity matrix. The symbol In can be used to indicate the nxn identity matrix. However, there seldom is any confusion when the subscript n is omitted.
Included among the computer programs is a program (makeequ = make equations). It askes for the number of unknowns and the solution to them. Then all coefficients are requested, line by line. The program prints out the coefficient matrix and the right hand column of values. For example, if the number of unknowns is 2, and the solution is 2 and 1, and the coefficients are 2 3 for the first row and 4 5 for the second row, the computer outputs (only the matrix of the equations)
2 3 7 (2x + 3y = 7)
4 5 13 (4x + 5y = 13)
It has calculated the column vector7 13Suppose now [7] is to be a solution to
6w + 7t = ? 8w + 9t = ??The computer will output:
6 7 133 (6w + 7t = 133) 8 9 173 (8w + 9t = 173)Then what has happened to the column vectors is:
2 => 7 => 133 1 13 173
The coefficient matrix can be used to determine if a system of linear equations can be solved.
This is done by evaluating a square matrix to get a specific number (in these discussions, an integer) that will determine the solvability. If the number is zero, then no unique solution exists, if not zero then there is a unique solution (the "normal" situation). One way to find this number is to try to solve the equations by converting the matrix of coefficients into the matrix of the form