Jim Sally Rich Frances Bob Jack Rose Violet Joseph Bill Ann JuneEach of the three rows has the names of 4 students. But each of the four columns has the names of 3 students. This table as size of 3x4 (3 by 4). It is customary to give the number of rows first, then the number of columns.
In Row 2 are Bob, Jack, Rose, Violet. In Column 4 are Frances, Violet, Bill. So Violet sits in Row 3 and Column 4. This location is denoted as [3,4]. The persons whose name begins with the letter J sit in seats at locations [1,1], [2,2], [3,1], [3,4].
In an intuitive sense, these location numbers in brackets locate the empty seats. If the table in [1] is given the name T then T[2,3] = Rose, T[3,4] = June. T gives the name of the person sitting in chair [ _,_ ] .
The teacher may want to interchange (swap) Row 2 and Row 3 to get a different table:
[2]
Jim Sally Rich Frances Joseph Bill Ann June Bob Jack Rose VioletIf this table [2] is given the name S, then S[2,3] = T[3,3].
A table may have (the names of) things of a common type placed at all the locations in it. In a table an entry has been placed at a location [1,1], an entry has been placed at [1,2], etc.This creates a table of entries, whatever they are. The most common entries in these discussions are integers and sometimes fractions which are quotients of integers (denominators not zero). For example,
[3]
2 1 -7 4 4 -3 1 5 -2 9 4 2This is another 3x4 table. Its entries are integers. A table of numbers is called a matrix. If it is desirable to give a name "A" to the matrix, then the notation becomes:
2 1 -7 4 A = 4 -3 1 5 -2 9 4 2
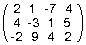
The arithmetical nature of a matrix allows their frequent applications to various fields of mathematics and other fields of science. They can be applied in particular to simultaneous linear equations. The word "simultaneous" implies two or more components of an event happening together, and all should be considered together. In simultaneous equations the same unknowns (letters) are used. The word "linear" implies simple unknowns, no exponents, no roots, no logarithms, no trigonometric functions, etc. The two simultaneous linear equations in x and y
[4]
Omit the symbols for unknowns and the equal signs in [4] and [5] produces the same 2x3 matrix of the equations:
[6]
3 4 10 3x + 4y = 10 2 5 9 2x + 5y = 9Multiply Row 1 by -2 and Row 2 by 3, and replace Row 3 by the result produces the matrix of the equations (in a shorter notation, Row 2 <-- -2(Row 1) + 2(Row 2)):
3 4 10 3x + 4y = 10 0 7 7 7y = 7Now divide the new Row 2 by 2 to get a new matrix:
3 4 10 3x + 4y = 10 0 1 1 y = 1Replace Row 1 by -4x(Row 2) + Row 1:
3 0 6 3x = 6 0 1 1 y = 1Divide Row 1 by 3 to get:
1 0 2 x = 2
0 1 1 y = 1
The solution is in the right column2 x = 2 1 y = 1
Notice that the row operations on the matrix of the equations correspond to legal operations on the equations.
Three rules of algebra for handling simultaneous liner Equations are useful here:
(E1) In any equation, every number may be multiplied by the same non-zero number.
(E2) Any two equations may be added together and this sum may replace either equation (but not both).
(E3) Any two equations may be interchanged.
The corresponding rules for handling Matrices of equations are:
(M1) In any row, every number may be multiplied by the same non-zero number.
(M2) Any two rows may be added together and this sum may repalce either row (but not both).
(M3) Any two rows may be interchanged.
No similar rules will apply here for the columns.
Applying the above rules changes the equations or matrix of the equations. In these discussions the symbol => will mean "rules for handling rows have been applied to produce." For example [6] - [10]may be written:
[12]
3 4 10 => 3 4 10 => 3 4 10 => 3 0 6 => 1 0 2 2 5 9 0 7 7 0 1 1 0 1 1 0 1 1Often the chains showing every conversion are long. Some of the intermediate matrices may be omitted. The equations
2 3 4 21 -1 0 0 -4 1 0 0 -4 5 4 2 44 => 0 -1 0 -7 => 0 1 0 7 1 7 6 41 0 0 1 2 0 0 1 -2For more detail click here.
It is quite possible that linear equations cannot be solved in the usual sense. For example, the simple equation
[15]
A similar situation may exist with simultaneous equations with 2 or more unknowns. A very obvious example is
[17]
The 0=0 result can be obtained from the equations
[18]
An attempt to solve the following equations leads to the contradiction like 0=1 (twice the first equation subtracted from the second equation):
[19]