Go to other chapters or to other branches of math
Additional Material for this Chapter
Exercises for this Chapter
Answers to Exercises
Computer programs
Chapter 6
Affine Transformations on the Plane
Section 1: Translations
In the last chapter actions involving the geometry of the plane were described using linear transformations: reflections about a line through the origin, reflections through the origin, rotations about the origin, projections upon a line through the origin. However, for these transformations to exist an origin must exist and every linear transformation must carry that origin onto itself. But the actions on the plane as studied in high school geometry require no origin. An important example is a translation.
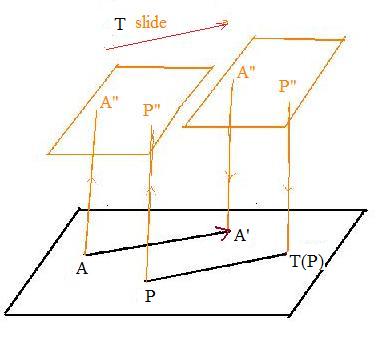 Consider now a vector AA' from a fixed point A to a fixed point A'. Copy the entire plane onto stiff paper, copying A onto a point A" on the paper. Slide the paper without rotation and without distortion (no shrinkange or expansion) and stop when A" comes on top of A'. Copy the entire paper back onto the plane. By this method the entire plane is copied back onto itself.
Consider now a vector AA' from a fixed point A to a fixed point A'. Copy the entire plane onto stiff paper, copying A onto a point A" on the paper. Slide the paper without rotation and without distortion (no shrinkange or expansion) and stop when A" comes on top of A'. Copy the entire paper back onto the plane. By this method the entire plane is copied back onto itself.
A function T can describe this copying. If P is any point in the plane, it is copied before movement onto the paper to produce point P" and after movement, back onto the plane to produce point P'. Let T(P) = P'.
For all points the given vector AA' shows where to move the paper after copying the plane. The vector shows how much to move the paper (the length of the vector) and in which direction (the direction in which the vector is pointing).
[1.1a] (Translation directed by a vector) A translation directed by a given vector is a function that carries every point onto an image such that the vector from the point to the image is equivalent to the given vector.
Notation: If AA' is a given vector, then vector from any point P to T(P) is equivalent to AA'. (Both vectors have the same length and both vectors point in the same direction.)
It is possible that image A' falls on top of A. In that case AA' is a zero vector. In that case the paper does not move. Every point P is carried onto itself T(P) = P. The translation becomes the identity transformation on the plane. Only this translation F can be a linear transformation I.. All other translations would move the orgin, if there is an origin. The translation (identity) that does not move anything will be called trivial.
Notice that the translation carries point A onto point A'. Suppose the translation carries points B,C,D,... onto points B',C',D',... Then by definition vectors BB' = CC' = DD' = ... = AA'. Actually, any of these vectors can serve as the vector that directs the translation. Moreover, the translation and the given vector determine each other completely. If the paper is not rotated nor distorted, then any point W before movement and the image W' of that copied point W" after movement can produce the given vector WW' where W' = T(W).
This motivates the following alternative definition:
[1.1b] (Translations) A function on the plane (or space) is a translation if and only if for every pair of points the vector from the first point to its image is equal to the vector from the second point to its image.
Notation: T is a translation if and only if the vector from P to T(P) is equal to the vector from Q to T(Q), for any points P and Q in the plane (or space).
Again let P' = T(P), and Q'=T(Q). If T is a translation then as vectors PP' = QQ' Therefore segments PP' and QQ' are parallel and congruent. Then PQQ'P are vertices of a parallelogram, and as vectors along the sides of this parallelogram PQ = P'Q'. Therefore, as segments PQ = P'Q'. This proves
[1.2] (Congruence) Every translation carries vectors onto equivalent vectors, and therefore preserves distance.
This means that congruence can exist outside the collection of linear transformations.
[1.3] (Orientation) Every translation on the plane preserves orientation of convex polygons.
Since the translation carries vectors onto vectors, it carries the sides of an oriented polygon onto the sides of the image, pointing in the same direction. Therefore, the polygon and its image have the same orientation. Intuitively speaking, translation preserves orientation because it does not flip any figure over, but slides the figure along the plane.
 Translations are functions, and therefore they can be combined using composition, also called multiplication. If T1 and T2 are translations then T2T1 is their product, where T1 acts first on any point. If P is any point, then T1 carries P onto the image point T1(P). Then T2 carries this point onto T2(T1(P)). This means that
T2T1 carries P onto T2T1(P).
Translations are functions, and therefore they can be combined using composition, also called multiplication. If T1 and T2 are translations then T2T1 is their product, where T1 acts first on any point. If P is any point, then T1 carries P onto the image point T1(P). Then T2 carries this point onto T2(T1(P)). This means that
T2T1 carries P onto T2T1(P).
Similarly, If T1 carries point A onto A' and T2 carries A' onto A", then T2T1 carries A onto A". This forms a vector addition triangle as shown in the adjacent figure.
All this means is that there is an isomorphism between translations and vectors. It is so "tight" that in some books and papers a vector is defined as a translation. In these discussions their distinction will be continued. Since vectors with addition can be added and subtracted, translations directed by them can be combined (multiplied). For example, if vector AA' directs translation T, then --AA' = A'A directs a translation in the opposite direction. That translation is the inverse and is denoted by T-1. This means that all translations are non-singular.
The identity I is a translation that does not move anything, and is directed by the zero vector AA.
The addition of vectors is commutative.
These observations lead up to the fact that
[1.4] (Translation group) The collection of all translations forms a commutative multiplicative group.
The above discussion describes a translation without any use of any origin. But this does not exclude an existence of an origin. If an origin O exists then it is possible to describe a translation using position vectors. A translation T must carry that O somewhere, namely onto the point T(O). Let O' = T(O). Let R be any point, and let R' = T(R) be the image of R. By definition [1.1b] the vectors RR' = OO'. Using position vectors, this is equivalent to r' - r = o'. Solving for r' produces the fundamental equation:
r' = r + o'
In words
[1.5] (Translations expressed by means of position vectors) Assume an origin exists. The translated image of any point is located by a position vector equal to the sum of the position vector locating the point and the position vector locating the image of the origin.
If each point is located also by an ordered pair, then let O'(α,β), R(x,y) and R'(x',y'). Then (x',y') = (x,y) + (α,β). These statements support the following:
[1.6] (Translation expressed by means of coordinates) Assume an origin exists. If ordered pairs (x,y), (x',y') and (α,β locate an arbitrary point, its translated image and the translated origin, then
x' = x + α y' = y + β
where (α,β) locates the image of the origin.
(In space the three equations are x' = x + α y' = y + β z' = z + γ) where
(α,β,γ) locates the image of the origin.)
Section 2: Lines, parallelism and proportionality
In the last section it was pointed out that non-trivial translations are not linear transformations. Yet they are geometric functions, carrying lines onto lines, parallelograms onto congruent parallelograms etc. In this section discussions will unite the "maverick" translations and linear transformations into one family of transformations. It is natural to use the geometric approach to do this because both effect the geometry of the plane in familiar ways.
The geometry in these sections is the classical geometry of the plane as studied in high school. However in some places there are statements which generalize some of the concepts developed for plane geometry to apply to space, which is classical solid geometry. In this chapter the plane is considered as sets of points, 'which collectively form a universe. For lack of a better name let this universe be known as the universe of plane geometry. Lines are proper subsets of this universe. However, the definitions (a few with slight modifications) and theorems of plane geometry are still true here and may be used to support discussions. In any discussion an origin does not exist unless specifically mentioned. Although vectors from points to points may be used, position vectors from the origin to points and linear transformations will not be used if there is no origin. To accommodate a possible absence of an origin, in section 3 below a more general type of geometric transformation (affine) will be defined to extend the actions that linear transformations did on a plane that may or may not have an origin.
 Lines, meaning straight and without ends, are special subsets this universe. Notation here is the word line with a subscript. Example: lineo. Lines may be parallel. Contrary to high school geometry a line here is allowed to be parallel to itself. Then the relation "is parallel to" becomes an equivalence relation among lines.
Lines, meaning straight and without ends, are special subsets this universe. Notation here is the word line with a subscript. Example: lineo. Lines may be parallel. Contrary to high school geometry a line here is allowed to be parallel to itself. Then the relation "is parallel to" becomes an equivalence relation among lines.
A unique line passes through any pair of distinct points. Those same points determine a segment which is the subset of all points on the line between and including the given pair of points. The given points then are called endpoints. It will be convenient to allow the endpoints to coincide producing a degenerate segment. A degenerate segment is actually a single point and therefore cannot determine a unique line.
Between two distinct points a vector can be formed. It has length and direction. Instead of a direction, orientation is given in some discussions here to a line segment determined by pairs of distinct points. Click here to see a discussion of orientations of segments.
Click here to see a simple geometric construction that establishes a one-to-one correspondence between any pair of parallel lines. This construction is used in the next discussions.
Much of geometry is based directly or ultimately on the real number line. That line was discussed in Volume A.
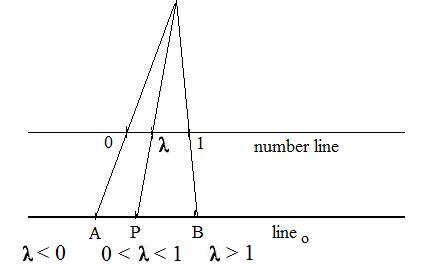 The numbers 0 and 1 locate distinct points on that line. On any given line lineo in the plane universe select two distinct points A and B. Insert the number line into the plane universe parallel to lineo so that segment 01 and segment AB have the same orientation. Then use the "simple geometric construction" mentioned above to establish a one-to-one correspondence between the real number line and the given line lineo. Then for any real number λ (on the number line) the one-to-one correspondence locates a unique point P on lineo.
The numbers 0 and 1 locate distinct points on that line. On any given line lineo in the plane universe select two distinct points A and B. Insert the number line into the plane universe parallel to lineo so that segment 01 and segment AB have the same orientation. Then use the "simple geometric construction" mentioned above to establish a one-to-one correspondence between the real number line and the given line lineo. Then for any real number λ (on the number line) the one-to-one correspondence locates a unique point P on lineo.
The point P may be located by a ratio of lengths of segments. Using the equation
AP = λAB
where AP and AB here denote the directed lengths of segments AP and AB. Then for different values of λ, (if λ is negative, then use PA)
λ < 0 means that A is between P and B (P is to the left of A)
λ = 0 means P = A
0 < λ < 1 means P is strictly between A and B
λ = 1 means P = B
λ > 1 means that B is between A and P (P is to the right of B)
For example, if λ = 1/2 then P is located on the midpoint of segment AB. The ratio of the lengths of the two segments AP and AB is equal to 1/2. (Equivalently, the ratio of the lengths of the segments AP and PB is 1.) Similarly, λ = 1/3 and λ = 2/3 locate the two points of trisection of segment AB. These two fractions are the ratios of the lengths of AP and AB for the two positions of P.
[2.1] (Proportionality coefficient locating a point) In the above construction, the real number λ locates a point P on the line through points A and B (relative to A and B). λ is called a proportionality coefficient.
Section 3: Geometric Functions of the Plane
Since the plane universe is a set of points, functions on that universe carry points onto points. Let F be any function on this universe. This means that if P is any point in the plane, then F(P) is a point back in the plane. If S is any subset of the plane then F(S) is also a subset of the plane, where F(S) is the totality of all points that are images of points in S. Recall that as a vivid description in these discussions, F carries the subset S onto the subset F(S).
If S is a recognizable geometric subset such as a line, segment, triangle, rectangle, circle, ... what does F(S) look like? Intuitively speaking, F "preserves geometric shapes" if for any subset S, F(S) has a shape that can be recognized somehow as resembling the shape of S.
[3.1] (Geometric functions) A function that carries the plane universe into itself is geometric if it carries
(a) every point of the plane onto a point of the plane
(b) every line in the plane onto a line or onto a point in the plane
Notation If F is a geometric function then the image F(lineo) is a line or a point.
In space, a geometric function carries every point onto a point in the same space; it carries all of space onto itself, or onto a plane, or onto a line, or onto a point; it carries any plane (in space) onto a plane, or onto a line or onto a point; it carries any line onto a line or onto a point.
Intuitively speaking, a geometric function preserves the straightness of a line, and will not carry a line onto a curve like a parabola or like the wavy sine curve. (There are "topological" functions that do this.)
[3.1s] (Preserving segment structure) If in addition to conditions (a) and (b) in [3.1] a geometric function carries segments onto segments, and their endpoints onto endpoints, then the function is called an s-geometric function.
Notation: If F is s-geometric then for segment AB, F(AB) = segment F(A)F(B). The usage of concept of s-geometric is temporary until [3.7] below, where a more widely used terminology is introduced.
An s-geometric function preserves betweenness: if P is between points A and B then P is a point on segment AB. and F(P) is on the segment F(A)F(B). Therefore, F(P) is between F(A) and F(B).
Allow two coincident points to be a segment of zero length. The s-geometric function picks up a segment, during the process of carrying it the segment may be stretched, shrunk or left unchanged, then put down somewhere but always in the form of a segment. This image segment and the original segment need not be parallel nor congruent.
[3.2] (Non-singular geometric functions) A geometric function that carries any entire line onto a point is said to be singular. A non-singular geometric function carries (entire) lines onto (entire) lines.
A non-singular s-geometric function carries triangles onto triangles, and in general polygons onto polygons with the same number of sides,
Remark: In 3 dimensional space a non-singular geometric function also carries planes onto planes. Intuitively speaking, non-singular geometric functions preserve the wholeness of a line, plane or space, and not shrink it to something smaller. A non-singular s-geometric function carries tetrahedrons onto tetrahedrons and in general, polyhedra onto polyhedra with the same number of vertices, edges and faces.
A segment has been described as part of a line that lies between two points on the line. There is a higher geometry (projective) in which the term between is not defined. Therefore segments are not defined there. But iIn HS geometry the concept of segment and betweenness is meaningful.
[3.3] (preserving parallelism) A geometric function preserves parallelism if it carries all parallel lines onto parallel lines.
There exist geometric functions that do not preserve parallelism. (They can be studied in a branch of mathematics called "Projecctive Geometry.")
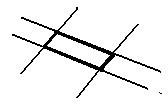 Suppose a pair of parallel lines intersect another pair of parallel lines in exactly 4 distinct points. If a non-singular s-geometric function F preserves parallelism then the image of these intersecting parallel lines is intersecting parallel lines. Clearly, F carries parallelograms onto parallelograms. It is possible to define a "collapsed" parallelogram as two line segments of the same length on the same line. Then
Suppose a pair of parallel lines intersect another pair of parallel lines in exactly 4 distinct points. If a non-singular s-geometric function F preserves parallelism then the image of these intersecting parallel lines is intersecting parallel lines. Clearly, F carries parallelograms onto parallelograms. It is possible to define a "collapsed" parallelogram as two line segments of the same length on the same line. Then
[3.4] (Carrying parallelograms onto parallelograms) A s-geometric function preserves parallelism if and only if it carries parallelograms onto parallelograms.
It should be pointed out that the parallelograms need not be congruent or even similar. In other words, the function need not preserve angles (need not carry angles onto congruent angles).
But a quadrilateral is a parallelogram if and only if the diagonals bisect each other.
[3.5] (Preserving midpoints) A s-geometric function preserves parallelism if and only if it carries the midpoint of every segment onto the midpoint of the image segment.
An inductive argument can be made to support the following statements:
a s-geometric function that preserves parallelism carries a partition of any segment into n congruent pieces onto a partition of the image segment into n congruent pieces. In particular, if n = 3 and If P is located 1/3 the way from A to B then F(P) is 1/3 the way from F(A) to F(B)
This statement motivates the following definition (λ locates the end points of the pieces of the partition):
[3.6] (Preserving proportionality) A s-geometric function F preserves proportionality if and only if for any pair of points A and B on any lineo and for any real number λ that locates a point P, then the same λ locates the corresponding image point F(P) on the image line F(lineo) through points F(A) and F(B).
Notation: if A' = F(A) and B' = F(B) and P' = P where A,B,C are collinear, then A',B',C' are collinear. Furthermore, if vector AP = λAB, then A'P' = λA'B' .
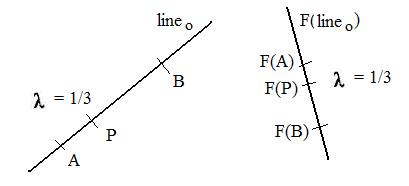
For example, if λ = 1/2, then λ locates the mid-points of both segments AB and A'B' which is F(AB). If λ = 1/3 or λ = 2/3 then λ locates the points of trisection of the two segments. If P is 4/5 the way from A to B, then F(P) is 4/5 the way from F(A) to F(B). If λ = 1 then P coincides with endpoint B, and F(P) coincides with endpoint F(B). If λ = 3/2 then P is outside segment AB and past B. Also F(P) is outside segment F(AB) and past F(B).
[3.7] (Affine transformations) A s-geometric function that preserves proportionality is said to be an affine transformation.
Affine transformations are a stronger form of s-geometric functions. They not only preserve betweenness, but the preserve proportionality where points are located. Simply take λ between 0 and 1. AP = λAB forces P to be between A and B. Similarly, A'P' = λA'B' forces P' to be between A' and B', where A' = F(A), B' = F(B'), P' = F(P).
[3.8] (Affine transformations and translations)
(a) All translations are affine transformations.
(b) An affine transformation is a translation if and only if it carries every vector onto an equivalent vector (pointing in the same direction and having the same length).
[3.9] (Affine transformations and linear transformations) Assume than an origin exists.
(a) All linear transformations are affine transformations.
(b) An affine transformation is a linear transformation if and only if it carries the origin onto itself.
Click here to see a discussion skupporting [3.9].
[3.10] (Products of affine transformations) The product of two affine transformations is an affine transformation.
Notation: if F1 and F2 are affine transformations then F2F1 is affine.
Let P,Q,R be points such that PR = λPQ. Let P' = F1(P), Q' = F1(Q), R' = F1(R), P" = F2(P'), Q" = F2(Q'), R" = F2(R'). Since F1 is affine then P'R' = λP'Q'. SInce F2 is affine, then P"R" = λP"Q". This means that F2F1 preserves proportionality.
[3.11] (Inverses of non-sisngular affine transformations) If an affine transformation is non-singular, then its inverse is an affine transformation.
Notation: if F is a transformation that is both non-singular and affine, then F-1 is affine.
Let P,Q,R be points such that PR = λPQ. Assume P and Q are distinct. Let P' = F-1(P), Q' = F-1(Q), R' = F-1(R). Then P' and Q' are distinct. But P'R' = σP'Q' for some real number σ. Since F is affine, it preserves proportionality. Therefore, PR = σPQ. Since PR is equal to both λPQ and σPQ, then λPQ = σPQ. Since Pand Q are distinct, then λ = σ. This proves that P'R' = λP'Q' and F-1 preserves proportionality.
[3.12] (Group of nonsingular affine transformations) The collection of all non-singular affine transformations form a group using the product of functions.
Since the identity transformation is affine and non-singular, then by [3.10] and [3.11] the collection forms a group. The collection of translations forms a proper subgroup of the collection of all distance preserving functions, which in turn forms a proper subgroup of the collection of all non-singular affine transformations. If an origin exists, then the collection of all non-singular linear transformations also forms a proper subgroup of the collection of all non-singular affine transformations.
Because it preserves midpoints, an affine transformation carries parallelograms onto parallelograms and preserves parallelism. It also preserves betweenness: if P is between A and B, then F(P) is between F(A) and F(B). 0 < λ < 1.
(In projective geometry there are geometric functions that do not preserve betweenness.)
The facts about affine transformations carrying parallelograms onto parallelograms and preserving proportionality suggest a relationship with linear transformations. Yet a non-trivial translation shows that an affine transformation on a plane (or space) with an origin need not carry that origin onto itself. (This also presents a problem of affine transformations carrying position vectors onto position vectors which do not locate the true images of points.) The relationship is expressed in the following, even if the affine transformation is not linear:
[3.13] (Affine transformations, linear transformations and translations) Assume that an origin exists. Any affine transformation on a plane or space is equal to the product of a translation and a linear transformation.
Notation: F = TL, where F is affine, T is a translation, and L is linear.
Let O' = F(O). The vector OO' determines and directs a translation T. Intuitively speaking, the inverse translation T-1 will carry the action of F back to action around the origin. It will be shown that this action at the origin is described by a linear transformation. T-1F carries the action of F back to arkound O. Let L = T-1F.
L carries the origin back onto itself: L(O) = T-1F(O) = T-1(O') = O
L is affine because L = T-1F and both F and T-1 are affine.
By [3.9b] L is a linear transformation.
[3.14a] (Affine subsets) A property of a subset of the plane is affine if for every affine transformation the image of that subset has that same property.
Notation: For every affine transformation F, S and F(S) have the same property.
Examples of affine subsets: segments, parallelograms, triangles, polygons, segments, points
More advanced examples: ellipses, parabolas, hyperbola, conic sections
Examples of subsets that are not affine: right triangles, rectangles, circles, angles, isosceles triangles.
Even though lines have meanings in projective geometry, "segments" are not defined.
[3.14b] (Affine relations) A relation between subsets of the plane is affine if for every affine transformation the images of those subsets has that same relation.
Notation: For every affine transformation F, and for every pair of subsets S1 and S2 if there is a relation between S1 and S2 then that relation exists between F(S1) and F(S2) have the same property.
Examples of affine relations: being parallel (lines), (points) being between other points
Examples of relations that are not affine: being congruent (figures), being similar (figures). being perpendicular (lines)
It is possible to create a consistent geometry from all relationships between subsets that are affine and omit those that are not, and include all affine relations and omit all those that are not. It is called affine geometry." High school geometry is a part of this geometry, since all affine subsets and relations are meaningfujl in that familiar HS geometry.
 Consider now a vector AA' from a fixed point A to a fixed point A'. Copy the entire plane onto stiff paper, copying A onto a point A" on the paper. Slide the paper without rotation and without distortion (no shrinkange or expansion) and stop when A" comes on top of A'. Copy the entire paper back onto the plane. By this method the entire plane is copied back onto itself.
Consider now a vector AA' from a fixed point A to a fixed point A'. Copy the entire plane onto stiff paper, copying A onto a point A" on the paper. Slide the paper without rotation and without distortion (no shrinkange or expansion) and stop when A" comes on top of A'. Copy the entire paper back onto the plane. By this method the entire plane is copied back onto itself. Translations are functions, and therefore they can be combined using composition, also called multiplication. If T1 and T2 are translations then T2T1 is their product, where T1 acts first on any point. If P is any point, then T1 carries P onto the image point T1(P). Then T2 carries this point onto T2(T1(P)). This means that
T2T1 carries P onto T2T1(P).
Translations are functions, and therefore they can be combined using composition, also called multiplication. If T1 and T2 are translations then T2T1 is their product, where T1 acts first on any point. If P is any point, then T1 carries P onto the image point T1(P). Then T2 carries this point onto T2(T1(P)). This means that
T2T1 carries P onto T2T1(P). Lines, meaning straight and without ends, are special subsets this universe. Notation here is the word line with a subscript. Example: lineo. Lines may be parallel. Contrary to high school geometry a line here is allowed to be parallel to itself. Then the relation "is parallel to" becomes an equivalence relation among lines.
Lines, meaning straight and without ends, are special subsets this universe. Notation here is the word line with a subscript. Example: lineo. Lines may be parallel. Contrary to high school geometry a line here is allowed to be parallel to itself. Then the relation "is parallel to" becomes an equivalence relation among lines.
 The numbers 0 and 1 locate distinct points on that line. On any given line lineo in the plane universe select two distinct points A and B. Insert the number line into the plane universe parallel to lineo so that segment 01 and segment AB have the same orientation. Then use the "simple geometric construction" mentioned above to establish a one-to-one correspondence between the real number line and the given line lineo. Then for any real number λ (on the number line) the one-to-one correspondence locates a unique point P on lineo.
The numbers 0 and 1 locate distinct points on that line. On any given line lineo in the plane universe select two distinct points A and B. Insert the number line into the plane universe parallel to lineo so that segment 01 and segment AB have the same orientation. Then use the "simple geometric construction" mentioned above to establish a one-to-one correspondence between the real number line and the given line lineo. Then for any real number λ (on the number line) the one-to-one correspondence locates a unique point P on lineo.
 Suppose a pair of parallel lines intersect another pair of parallel lines in exactly 4 distinct points. If a non-singular s-geometric function F preserves parallelism then the image of these intersecting parallel lines is intersecting parallel lines. Clearly, F carries parallelograms onto parallelograms. It is possible to define a "collapsed" parallelogram as two line segments of the same length on the same line. Then
Suppose a pair of parallel lines intersect another pair of parallel lines in exactly 4 distinct points. If a non-singular s-geometric function F preserves parallelism then the image of these intersecting parallel lines is intersecting parallel lines. Clearly, F carries parallelograms onto parallelograms. It is possible to define a "collapsed" parallelogram as two line segments of the same length on the same line. Then
