(i) Vectors OP' = -- OP
(ii) Only the origin is carried back onto itself (left fixed); for all other points, P' and P are distinct
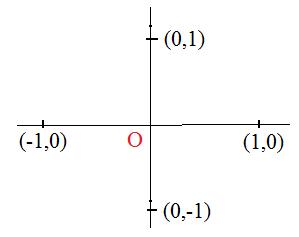
The first and second actions [3.1] and [3.2] introduce these ideas.
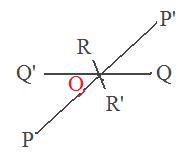 For any point not on the origin there is a line through that point and the origin. Push the point through the origin. On the other side of the origin go and stop when the image point will be the same distance from the origin as the original point.
For any point not on the origin there is a line through that point and the origin. Push the point through the origin. On the other side of the origin go and stop when the image point will be the same distance from the origin as the original point.
[3.1a] (Reflection through the origin) The origin is the midpoint of the segment joining any point and its reflection through the origin.
Notation: if P' is the image obtained by reflecting a point P through the origin, then O is the mid point of segment PP'.
[3.1b] Some immediate results of [3.1a]:
(i) Vectors OP' = -- OP
(ii) Only the origin is carried back onto itself (left fixed); for all other points, P' and P are distinct
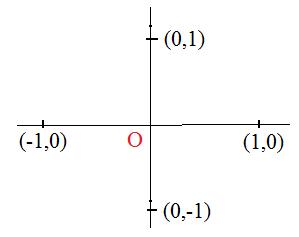
[3.1c] (Images of the special points and triangle)
(i) the images of (1,0) and (0,1) are (-1,0) and (0,-1) respectively;
(ii) the special triangle has vertices O, (1,0), (0,1). Its image has vertices
O, (-1,0), (0,-1);
(c) the orientation of the image triangle is positive (counter-clockwise).
It is obvious that O is the mid point of the segment joining (1,0) and (-1,0)
and the segment joining (0,1) and (0,-1).
The following matrix is formed from the transposes of these images:
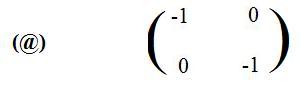
[3.1d] (The reflection through the origin is a linear transformation) The linear transformation L defined by
Since the images of (1,0) and (0,1) are (-1,0) and (0,-1) respectively, L(1,0) = (-1,0) and L(0,1) = (0,-1).
The equation for L(x,y) is derived from L(x,y) = xL(1,0) + yL(0,1) = x(-1,0) + y(0,-1) = (-x,-y).
To prove that L is the reflection through the origin, see where the mid point of (x,y) and L(x,y) lies.
(x,y) + L(x,y) = (x,y) + (-x,y) = (x + (-x), y + (-y)) = (0,0). Therefore (1/2) [(x,y) + (-x,y)] = (0.0). Hence origin O is the mid point of the segment joining (x,y) and L(x,y).
----------
 hspace=1000
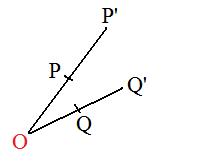
Suppose the magnification pushes P and Q to new points P' and Q' twice as far from the origin, so that
hspace=1000
Suppose the magnification pushes P and Q to new points P' and Q' twice as far from the origin, so that
More generally, any positive real number λ can be used in place of 2:
[3.2a] (Similitude) The action of obtaining a point P' from an arbitrary point P by the vector equation (*) is called a similitude with center at the origin and with coefficient λ, a positive real number..
[3.2b] For various values of λ the geometric effects are:
(i) if λ > 1, then image P' is further from the origin than P. This similitude is a niform dilation of the plane about the origin;
(ii) if λ = 1, then P'=P and the image of any point coincides with tht point. The similitude is the identity function on the plane, and no dilation nor contraction occurs;
(iii) if λ < 1 (but λ > 0) then image P' is closer to the origin than P. This similitude is a uniform contraction of the plane about the origin;
A similitude is completely determined by its coefficient. In fact the collection of all similitudes is in one-to-one correspondence with all the positive real numbers. That collection of similitudes is actually a group.
(i) if one similitude is followed by another the result is a similitude whose coefficient is the product of the two similitudes of the component similitudes;
(ii) the identity function is a similitude with coefficient 1;
(iii) the inverse of a similitude is a similitude whose coefficient is the inverse of the first similitude.
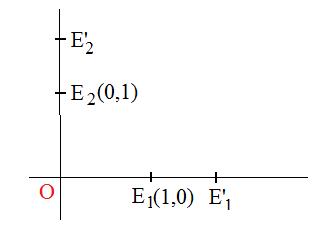
[3.2c] (Images of the special points) A similitude with coefficient λ carries the points (1,0) and (0,1) onto the points (&lambda, 0) and (0,λ) respectively.
If E1 and E2 are the special points (1,0) and (0,1) spectively, and E'1 and E'2 are the images by action of the similitude, then (position vectors)
From the transposes of the images of the special points the following matrix is formed:
[3.2d] (A similitude with center at the origin is a linear transformation) The linear transformation L defined by
Let P(x,y) and P'(λx,λy). Since (λx,λy) = λ(x,y), OP' = λOP. Therefore, L is a similitude with coefficient λ.
[3.2e] (Parallel image) A similitude carries segments onto parallel segments.
Notation: If P' and Q' are images of points P and Q respectively, then segment P'Q' is parallel to segment PQ.
Vectors OP' = λOP and OQ' = λOQ. Converting these vectors to position vectors
[3.2f] (Preserving angles) A similitude carries intersecting lines onto intersecting lines in such a way that the angle of intersection of the second pair of lines is congruent to the angle of intersection of the first pair.
Notation: If points A', B', C' are images of points A, B, C then angle A'B'C' is congruent to angle ABC.
By [[3.2e] segment A'B' and B'C' are parallel to AB and BC respectively. Therefore angle A'B'C' is congruent to angle ABC.
However, similitudes do not preserve lengths of segments. The images of segments are not necessarily congruent to the segments.

 Figure Fig 1a shows a right triangle ABC drawn on the right half of a piece of paper. Suppose ink for the triangle has not dried. The paper will be folded along the vertical line which divides the paper into two halves. As a result the ink on the right triangle touches the left half of the paper and leaves a copy of a right triangle there. If the paper is unfolded and made flat again then there are two right triangles. (Fig 1b) The triangle A'B'C' on the left is a reflection of the triangle on the right about the vertical line where the paper had been folded.
Figure Fig 1a shows a right triangle ABC drawn on the right half of a piece of paper. Suppose ink for the triangle has not dried. The paper will be folded along the vertical line which divides the paper into two halves. As a result the ink on the right triangle touches the left half of the paper and leaves a copy of a right triangle there. If the paper is unfolded and made flat again then there are two right triangles. (Fig 1b) The triangle A'B'C' on the left is a reflection of the triangle on the right about the vertical line where the paper had been folded.
Upon comparison of the two triangles, two observations can be made.
(a) the copy on the left side of the paper is congruent to the original triangle on the right side;
(b) the copy has an orientation opposite to the orientation of the original triangle on the right side.
The vertices of the original triangle on the right side are labeled A,B,C in a counter-clockwise direction. But the labels on the copy A',B',C' are given in a clockwise direction. The process of reflecting the original triangle about the vertical line makes a congruent figure but reverses orientation.
 This time a not-yet-dried parallelogram ABDC is located in the upper half of another paper, and a horizontal line is drawn below it. The paper is folded along the horizontal line to produce a copy of the parallelogram A'B'C'D' in the lower half of the paper. (Fig 2). A reflection about the horizontal line has occurred. The parallelograms are congruent but have opposite orientation.
This time a not-yet-dried parallelogram ABDC is located in the upper half of another paper, and a horizontal line is drawn below it. The paper is folded along the horizontal line to produce a copy of the parallelogram A'B'C'D' in the lower half of the paper. (Fig 2). A reflection about the horizontal line has occurred. The parallelograms are congruent but have opposite orientation.
In both examples it is the action of producing the copies that is the focus of these discussions. First is a geometric description of the action that reflects the triangle about the vertical line (Fig 1b). If a horizontal line segment is drawn joining points A and A' (vertices of the triangles) then the vertical line is the perpendicular bisector of segment AA'. Similarly, it is the perpendicular bisector of horizontal segments BB' and CC'. In general, if P is any point, then its image P' determines a horizontal segment PP' of which the vertical line is a perpendicular bisector.
Now to derive the formula for the linear transformation that does the reflecting of the triangle. The lintr requires the environment of the coordinate plane where each point has a label, an array of length 2. Place the original right triangle in the first quadrant of the coordinate plane and the vertical line on the y-axis. Since the vertices are points, they have attached labels, say
[3.3a] (Orthogonal reflection L about the y-axis)
geometric definition L(P) = P' where the y-axis is the perpendicular bisector of segment PP' or P=P' if point P is on the y-axis.
algebraic definition L(x,y) = (-x,y).
The algebraic definition makes L a linear transformation, since the expressions inside (-x,y) are linear expressions.
The derivation of the formula for the lintr that reflections the parallelogram about the horizontal line (Fig 2) is obtained in a similar way. But in this case the horizontal line is the perpendicular bisector of vertical segments AA', BB', CC' DD'. Place the original parallelogram in the first quadrant of the coordinate plane and the horizontal line on the x-axis.
[3.3b] (Orthogonal reflection L about the x-axis)
geometric definition L(P) = P' where the x-axis is the perpendicular bisector of segment PP' or P=P' if point P is on the x-axis.
algebraic definition L(x,y) = (x,-y).
The algebraic definition makes L a linear transformation, since the expressions inside (x,-y) are linear expressions.
Of course, this lintr is different from the lintr that is a reflection about the y-axis described in [3.1a]..
The reflections about the xaxis and the y-axis are linear transformations. Therefore, they have associated matrices. These matrices are obtained from what happens to the special points (1,0) and (0,1). The reflection about the y-axis carries these points onto (-1,0) and (0,1) respectively. Then the transposes of these images become the columns in the associated matrix.
The reflection about the x-axis carries the special points (1,0) and (0,1) onto (1,0) and (0,-1) respectively. Then the transposes of these images become the columns in the associated matrix.
[3.3c] (Associated matrices for the orthogonal reflections about the axes:
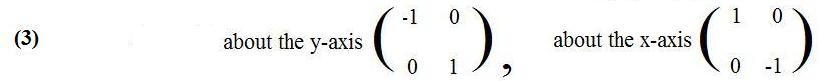
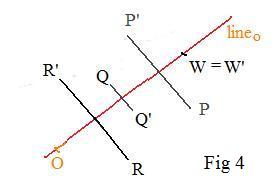
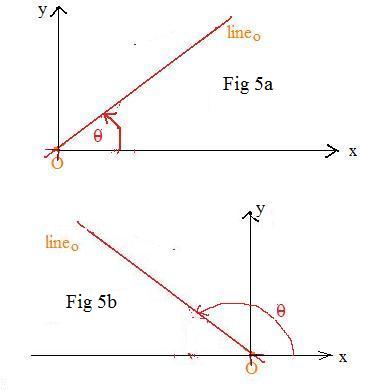 It is obvious that the position and location of the axis completely determines the reflection. The axis may be placed as a lineo in the coordinate plane so that it passes through the origin O. Let θ be the inclination angle as shown. If θ is between 0° and 90° then lineo slants from lower left to upper right (Fig 4a). If lineo is between 90° and 180° then lineo slants from lower right to upper left (Fig 4b). There is no need to consider angles between 180° and 360° because θ and θ - 180° determine the same lineo.
It is obvious that the position and location of the axis completely determines the reflection. The axis may be placed as a lineo in the coordinate plane so that it passes through the origin O. Let θ be the inclination angle as shown. If θ is between 0° and 90° then lineo slants from lower left to upper right (Fig 4a). If lineo is between 90° and 180° then lineo slants from lower right to upper left (Fig 4b). There is no need to consider angles between 180° and 360° because θ and θ - 180° determine the same lineo.
Any orthogonal reflection about a line through the origin must reflect the special points (1,0) and (0,1) about that line. In [3.3d] and [3.3e] that follow assume that the line passes through the origin and has an inclination angle θ.
[3.3d] (Reflected images of the special points) A reflection about the line with inclination angle θ carries (1,0) and (0,1) onto the points
Click here to see a discussion supporting this statement.
[3.3e] (Reflection is a linear transformation) The linear transformation L defined by
Click here to see a discussion supporting this statement.
Statements [3.3d] and [3.3e] combine to support the following:
[3.3f] (Orthogonal reflection about any line through the origin)
geometric definition If P' is the reflected image of any point P then the line is the perpendicular bisector of segment PP', or P=P' if point P is on the line (Fig 4).
algebraic definition The matrix associated with the orthogonal reflection about a line through the origin and making an inclination angle θ with the positive x-axis is

The associated matrix comes directly from [3.3d].
If θ = 90° then lineo is the y-axis. The associated matrix (6) becomes the first matrix in (3) above.
If θ = 0° or θ = 180° then lineo is the x-axis. The associated matrix (6) becomes the second matrix in (3) above.
If θ = 45° then lineo bisects the angle between the positive x-axis and the positive y-axis. The reader can replace θ in the formula for L in [3.1e] by 45° (dont forget to double this angle to 90°) and obtain: L(x,y) = (y,x). Therefore L interchanges the coordinates. What is the matrix associated with L ?
A precise geometric definition of a rotation is not given here. It would not be in the spirit of an intuitive introduction to rotations. Instead two equivalent intuitive descriptions [3.4a] and [3.4b] are given below.
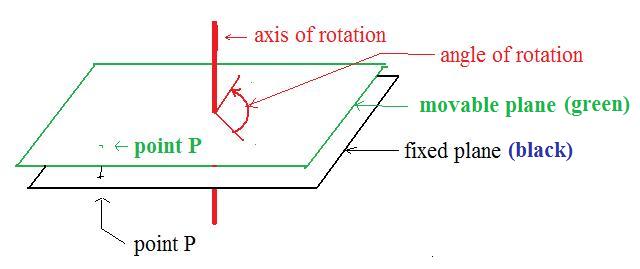 [3.4a] (Intuitive geometric description 1) Keep in mind that the rotation function on the plane carries points onto points in a definite manner. The plane does not move, so it will be called the fixed plane. A second plane is invented to carry out the motion of rotation. It is called the plane(See adjacent figure.) It lies above the fixed plane. There is a hole just above the origin in the other fixed plane. An axis is created perpendicular to the fixed plane and runs through the hole.
[3.4a] (Intuitive geometric description 1) Keep in mind that the rotation function on the plane carries points onto points in a definite manner. The plane does not move, so it will be called the fixed plane. A second plane is invented to carry out the motion of rotation. It is called the plane(See adjacent figure.) It lies above the fixed plane. There is a hole just above the origin in the other fixed plane. An axis is created perpendicular to the fixed plane and runs through the hole.
Suppose this plane is empty. Then each point P in the fixed plane is copied vertically into the movable plane above it to make a point P. After all the points have been copied from the fixed plane, the movable plane is rotated through a given angle. If the angle is positive then the rotation is done counter-clockwise. If the angle is negative then the rotation is clockwise. Each point P is carried along with the rotating movement. After the rotation of the movable plane is completed, then P is above some point P' in the fixed plane. (The new position of the movable plane and point P' are not shown in the figure.)
The rotation function on the fixed plane carries P onto P'.
The phrase "rotation function on a plane" is less common that the phrase "rotation of the plane". The reader may mentally attached the word "function" to the word "rotation" whenever it occurs alone in this section.
The above description places the two parallel planes in three dimentional space. The following is an equivalent description of the rotation function in the two dimentional (fixed) plane, and does not involve any rotating (green) plane. But it does involve an arbitrary point P in the (fixed) plane to be carried onto a point P' in that same plane. It is this description that will lead to a more rigorous algebraic definition of a rotation.

[3.4b] (Intuitive geometric description 2) With one end point fixed on the origin O swing segment origin OP around in a circular motion through angle θ and stop. Then the segment origin OP' is formed. The point P' is the rotated image of point P. If θ is positive, the the motion is counter-clockwise (Fig 1a). If θ is negative then the motion is clockwise (Fig 1b).
[3.4c] There are several immediate results from this description:
(i) The angle completely determines the rotation.
(ii) Any point and its rotated image are the same distance from the origin.
(iii) If θ = 0, there is no motion. Then P' = P. The identity function I is a rotation through an angle of zero.
(iv) The rotation of any point about the origin through an angle of θ is equivalent to a rotation of that same point through an angle of θ - 360°.
(v) The rotation through any number of revolutions, positive or negative, carries each point back onto itself.
(vi) A rotation through an angle -180° is equivalent to a rotation through an angle of 180°.
The proof of the following important statement is almost trivial:
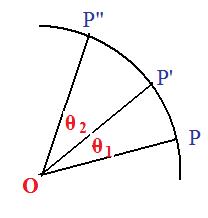
[3.4d] (Combining rotations) If a pair of rotations act on a plane, then the angle of the combined rotations (one acting after the other) is equal to the sum of the angles of the individual rotations.
Notation: If θ1 and θ2 are the angles of the two rotations, then their combined action (composition) is a rotation with an angle of θ1 + θ2.
The first rotation carries point P onto point P', and the second rotation carries point P' onto P".
The angles involved with rotations are real numbers, which are commutative. This makes the combinedaction of any two rotations commutative - either rotation may act first.
Since θ + -θ = 0, every rotation has an inverse. Simply rotate the same amount but in the opposite direction.
[3.4e] The collection of all rotations about the origin form a commutative group.
It is time now to derive the formula for a rotation. First the images of the special points (1,0) and (0,1) are calculated.
[3.4f] (Rotated images of the special points) A rotation through angle θ carries points (1,0) and (0,1) onto the points
Click here to see the discussion supporting this statement.
From the transpose of coordinates of image points form the matrix

[3.4g] (General formula for rotation) The linear ttransformation L defined by
Click here to see the discussion supporting this statement.
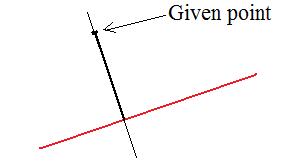 One of the important constructions in plane geometry is to construct a line through a given point and perpendicular to a given line. (Only a compass and straight edge can be used.)
One of the important constructions in plane geometry is to construct a line through a given point and perpendicular to a given line. (Only a compass and straight edge can be used.)
[3.5a] (Geometric description) Where the line through the given point intersects the given line perpendicularly is the point called the orthogonal projection of the given point upon the given line. (If the given point is already on the given line then the point is also the orthogonal projection upon the given line.) Do this action for every point in the plane.
Clearly the line segment joining the given point and its projected image is perpendicular to the given line.
[3.5b] Some obvious results of [3.5a]
(i) The location and position of a given line completely determine the orthogonal projection of the entire plane onto it.
(ii) The image of a line or line segment perpendicular to the given line is a point.
(iii) Parallel line segments not perpendicular to the given line are projected onto congruent segments inside the given line.
(iv) A projection carries subsets of 2 dimensions (have langth and width) onto subsets of lesser dimension (as usbsets of the given line).
(v) There is no inverse action to undo the action of a projection.
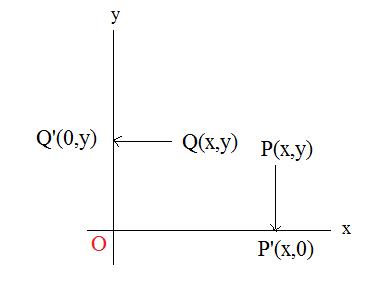 Two simple orthogonal projects occur in the coordinate plane if the given lines are the axes. In Fig 3 the arbitrary point P(x,y) is orthogonally projected onto the x-axis, and the arbitrary point Q(x,y) is orthogonally projected onto the y-axis. It is not difficult to determine the image points, namely P'(x,0) and Q'(0,y). (The second coordinate of every point on the x-axis must be 0. The first coordinate of every point on the y-axis must be 0. The projections are vertical and horizontal respectively.)
Two simple orthogonal projects occur in the coordinate plane if the given lines are the axes. In Fig 3 the arbitrary point P(x,y) is orthogonally projected onto the x-axis, and the arbitrary point Q(x,y) is orthogonally projected onto the y-axis. It is not difficult to determine the image points, namely P'(x,0) and Q'(0,y). (The second coordinate of every point on the x-axis must be 0. The first coordinate of every point on the y-axis must be 0. The projections are vertical and horizontal respectively.)
The vertical projection onto the x-axis of the special points (1,0) and (0,1) is (1,0) = (1,0) (point is already on the x-axis) (0,1) ---> (0,0), (point (0,1) is above the origin). Also the horizontal projection onto the y-axis of (1,0) and (0,1) produces images (0,0) and (0,1).
>b>[3.5c] (Images of the special points) The images of (1,0) and (0,1) projected orthogonally onto the x-axis and y-axis are (1,0), (0,0) and (0,0), (0,1) respectively.
The matrices from the transposes of these images are:
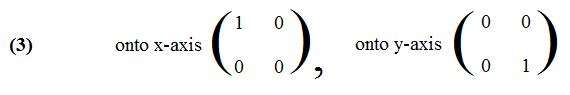
[3.5d] (Formula for projection onto the axes) The linear ttransformations L1 and L2 defined by
Click here to see an argument supporting this statement.
From the transposes of the images of the special points the following matrix is obtained:

Click here to see an argument supporting this statement.
A projection onto a line is singular because it has no inverse. There is no linear transformation that will undo what a projection has done. This is confirmed by the determinant of (4) which is zero. However, the matrix in (4) has rank 1, making projections onto lines having rank 1. See [2.7] above.