Here are three linear expressions in x and y :
  α1x + β1y,   α2x + β2y,   α3x + β3y
where α's, β's and γ's are coefficients. The three expressions can be used to define a linear transformation F as
F(x,y) = (α1x + β1y,   α2x + β2y,   α3x + β3y)
F is a linear transformation from a plane into space.

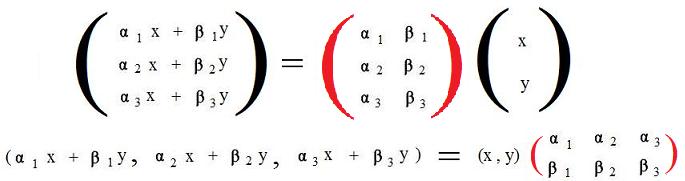
It is easily verified that the images of the special arrays (1,0) and (0,1) for this linear transformation are

F(1,0) = (α1, α2, α3)    and    F(0,1) = (β1, β2, β3)

The reader can easily verify the following two identities:

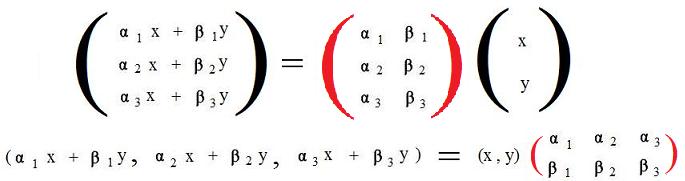
The top identity involves a 3x2 matrix whose rows are the coefficients of the three expressions. (This process was discussed in the previous section.) The bottom identity involves a 2x3 matrix whose two rows are the coordinates of the images F(1,0) and F(0,1). It is obvious that the 3x2 and 2x3 matrices are transposes of each other.

Let M = 3x2 matrix in the top identity. Then the transpose M' = 2x3 matrix in the bottom identity. It could be said that M is the matrix obtained direcctly from the (coefficients of) the arrays, but M' is obtained from images of the special arrays. Using the definition of F, F(x,y) = (x,y)M' . (Equations such as this motivate some algebraist to rearrange the notation of a function to (x,y)F.) This arrangement is more compatible with the usual function notation, since F carries horizontal arrays onto horizontal arrays.

[2.x] (Composition and product) Let F be a linear transformation from a first linear objecct into a second linear object, and let G be a linear transformation from the second linear object into a third linear object. If M' is the matrix corresponding to F and N' is the matrix corresponding to G, then the matrix corresponding to the composition GF is the matrix product M'N'.