The term "homogeneous" more accurately describes the linear expressions that will be discussed. But it will most often be omitted.
It is easy to extend this definition to include linear expressions in more variables, like x,y,z,w,... .However, this will not be done. Instead, discussions will involve only algebraic ideas that relate directly to the familiar geometric objects of point, line, plane and (3-dimensional) space.
In most discussions the coefficients of expressions will be integers, or, occasionally, rational numbers.
It is simple to find values for the linear expressions
(matrix) M = 5 6
8 -7
The following shows the details for the equation M(x,y)' = (5x+6y,8x-7y)' :
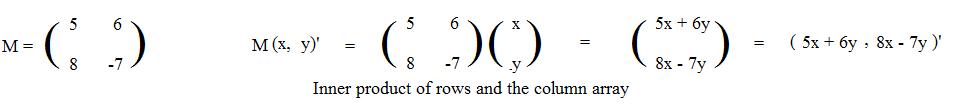
(5,6) * (x,y)' = 5x + 6y
(8,-7) * (x,y)' = 8x - 7y
Intuitively speaking, M and F do the same thing to points in the plane. More exactly, M and F perform the same action on the coordinates of every point in the plane.
1 2 3
(matrix) M = 4 5 6
7 8 9
The reader can verify that the product M(x,y,z)' = (x+2y+3z,4x+5y+6z,7x+8y+9z)'.
2 3
(matrix) M = 5 -2
-4 1
For example,
[1.2] (Corresponding functions) The correspoinding function F for a matrix M is obtained by defining F by F(x,y) = (linear array in x and y with coefficients from row 1 of M, linear array in x and y with coefficients from row 2 of M,....). If three variables are involved, F(x,y,z) = (linear array in x,y and z with coefficients from row 1 of M, linear array in x,y and z with coefficients from row 2 of M,....)
Subsets of geometric points can form recognizable objects: lines, circles, squares, cones,... . Some of these objects are more fundamental to discussions here: points, lines, planes, entire 3 dimensional space. They may be called basic affine objects. They have dimensions 0,1,2, and 3 respectively. They are fundamental parts of the subjects of plane and solid geometry. If they contain special points called origins, then they are basic linear objects. The term "basic" will often be omitted in these discussions.
Since linear objects have origins, position vectors exist. These have been denoted by p,q,r which locate points P,Q,R and can be expressed as p = OP, q = OQ, r = OR. For a geometric motivation for linear transformations click here.
[2.1] (Linear transformations) A function F from a linear object to a linear object is a linear transformation if and only if it satisfies the following two conditions:
(a) F(p + q) = F(p) + F(q); (homomorphism)
(b) F(λp) = λF(p) (homogeneous)
where p and q are any (position) vectors in the first linear object and λ is any real number.
Example:
Consider the function F from any linear object onto itself, defined by F(p) = 2p, for every point P in the first linear object.. Then F(q) = 2q, F(r) = 2r for position vectors q,r.... Intuitively speaking, F stretches any position vector to another vector pointing in the same direction but twice the length. F satisfies both conditions (a) and (b) of [2.1]:
(a) F(p + q) = 2(p + q) = 2p + 2q = F(p) + F(q).
(b) F(λp) = 2(λp) = λ(2p) = λF(p).
The following is a generalization of the defintion [2.1] of a linear transformation.
[2.2] Every linear transformation carries any linear combination of position vectors onto a linear combination orf position vectors.
Notation: If F is a linear transformation then F(λp + σq + ... + ωr) =
λF(p) + σF(q) + ... + ωF(r).
In a linear object position vectors locate points, and to those points are "attached" linear arrays. Therefore, linear arrays can be represented by position vectors. If a position vector p in a plane locates a point P(x,y), then p = (x,y). Similarly, if p in space locates point P(x,y,z) then p = (x,y,z). As a result,definition [2.1] may be stated for linear arrays by replacing p and q by their equals (x1,y1) and (x2,y2): F(p) = F(x1,y1), and F(q) = F(x2,y2). Similarly if F is from space: F(p) = F(x1,y1,z1), and F(q) = F(x2,y2,z2). (Here the two F's denote different functions because they involve different linear objects, namely plane and space.)
Example: The function F defined by F(x,y) = (x + y, x - y) is a linear transformation from a plane onto itself. It carries point (1,1) onto point (2,0), point (5,3) onto (8,2). Click here to see the proof that it satisfies both conditions
The following functions F,G,H are also linear transformations:
[2.3] A function from a plane into a linear object is a linear transformation if and only if carries an arbitrary point (x,y) onto a point whose coordinates are linear expressions of x and y. A function from space is a linear transformation if and only if it carries an arbitrary point (x,y,z) onto a point whose coordinates are linear expressions of x,y and z.
The pair of special unit arrays in a plane (1,0) = i and (0,1) = j as well as the triple of special unit arrays in space (1,0,0) = i, (0,1,0) = j and (0,0,1) = k play special roles with linear transformations.
Example: suppose F(1,0) = (4,5) and F(0,1) = (6,7). Onto what point does F carry the arbitrary point (x,y)? Notice that array (x,y) = x(1,0) + y(0,1). Then F(x,y) = xF(1,0) + yF(0,1) = x(4,5) + y(6,7) = (4x + 6y, 5x + 7y). Therefore, F carries the arbitrary point (x,y) onto the point (4x + 6y, 5x + 7y). This fact completely defines and determines F.
[2.4a] (Linear transformation from the plane is determined by images of two special points) From the identity
[2.4b] (Linear transformation from space is determined by images of three special points) From the identity
The expression xF(1,0) + yF(0,1) is actually an array whose coordinates are linear expressions in x and y. If F(1,0) = (α1, β1) and F(0,1) = (α2, β2) then
The coefficients of the linear expressions in (#) and (##) can be collected into matrices M2 and M3:
[2.5a] (Linear transformations from a plane into itself and 2x2 matrices) If F is any linear transformation from a plane into a linear object then F(x,y)' = M(x,y)' where M is the matrix
(matrix) M = coordinates of F(1,0) coordinates of F(0,1)
[2.5b] (Linear transformations from space into itself and 3x3 matrices) If F is any linear transformation from space into a linear object then F(x,y,z)' = M(x,y,z)' where M is the matrix
coordinates of F(1,0,0) (matrix) M = coordinates of F(0,1,0) coordinates of F(0,0,1)
Suppose F is the linear transformation defined by F(x,y) = (3x + 4y, 5x + 6y). F(1,0) = (3(1) + 4(0), 5(1) + 6(0)) = (3,5),
and F(0,1) = (4,6)
========================================
In most situations the definition of a linear transformation requires coordinates. If F is defined as F(x,y) = (2x,3y) then F is a function from a plane onto itself). In words, for the array associated with a point, F doubles the first coordinate, whatever it is, and F triples the second coordinate, whatever it is.
To show F is a linear transformation, it is necessary to show conditions (a) and (b) of [2.1]. Let
For condition (a)
For condition (b)
[2.2] A linear transformation carries lincombs onto lincombs.
Let F be a linear transformation, and let αp + βq + γr + ... be any lincomb of vectors p, q, r, ... . Then
[2.3] If the coordinates of the image points of a function F(x,y) are linear expressions of x and y, then F is a linear transformation from a plane into (possibly onto) a linear object. Similarly, if the coordinates of the image points of a function F(x,y,z) are linear expressions of x,y,z, then F is a linear transformation from space into (possibly onto) a linear object.
Notation:
if F(x,y) = αx
then F is a linear transformation from a plane to a point (origin)
If F(x,y) = (α1x + β1y, α2x + β2y)
then F is a linear transformation from a plane to itself, a line in that plane or a point (origin)
if F(x,y,z) = (α1x + β1y + γ1z, α2x + β2y + γ2z, α3x + β3y + γ3z)
then F is a linear transformation from space to itself, to a plane in that space, to a line in that space or to a point (origin).
Recall that the position vectors
(matrix) M = F(1,0) F(0,1) and (matrix) F(1,0,0) M = F(0,1,0) F(0,0,1)Then
F(x,y) = M(x,y)' and F(x,y,z) = M(x,y,z)'