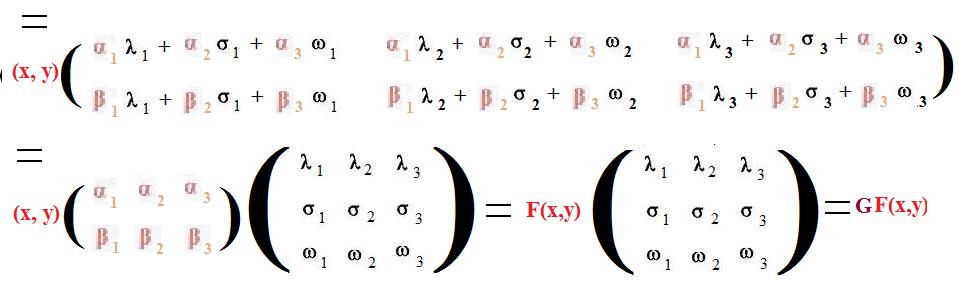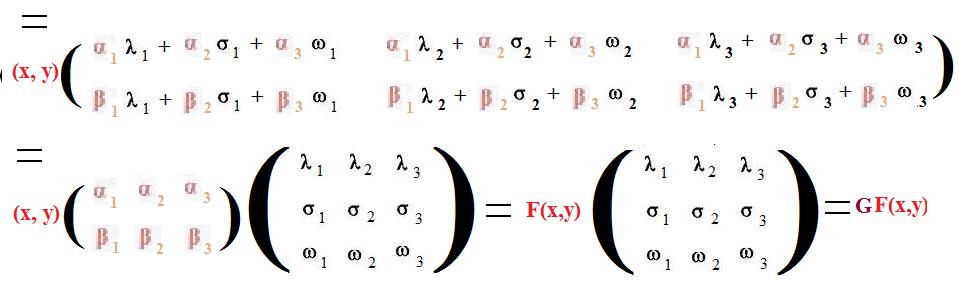The theorem is proven for the composition GF of linear transformations F: plane into space, and G: space into space. (Proofs for linear transformations between other linear objects are similar.) The most general forms for these linear transformations are:
F(x,y) = (α1x + β1y,
α2x + β2y,
α3x + β3y)
and
G(x,y,z) = (λ1x + σ1y + ω1z,
λ2x + σ2y + ω2z,
λ3x + σ3y + ω3z)
To form the composistion GF
replace every black x in G by (α1x + β1y),
replace every black y in G by (α2x + β2y),
replace every black z in G by (α3x + β3y) to get
GF(x,y)
=
(λ1(α1x + β1y) + σ1(α2x + β2y) + ω1(α3x + β3y),
[first or x- coordinate of the image of GF(x,y)]
λ2(α1x + β1y) + σ2(α2x + β2y) + ω2(α3x + β3y),
[second or y-coordinate of the image of GF(x,y)]
λ3(α1x + β1y) + σ3(α2x + β2y) + ω3(α3x + β3y))
[third or z-coordinate of the image of GF(x,y)]
=
((α1λ1 +
α2σ1 +
α3ω1)x
+
(β1λ1 +
β2σ1 +
β3ω1)y,
[first or x- coordinate of the image of GF(x,y)]
(α1λ2 +
α2σ2 +
α3ω2)x
+
(β1λ2 +
β2σ2 +
β3ω2)y,
[second or y- coordinate of the image of GF(x,y)]
(α1λ3 +
α2σ3 +
α3ω3)x
+
(β1λ3 +
β2σ3 +
β3ω3)y)
[second or y- coordinate of the image of GF(x,y)]