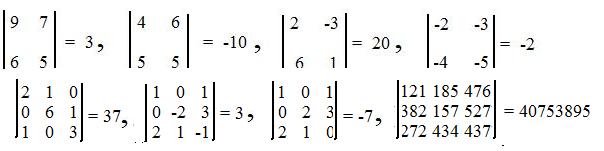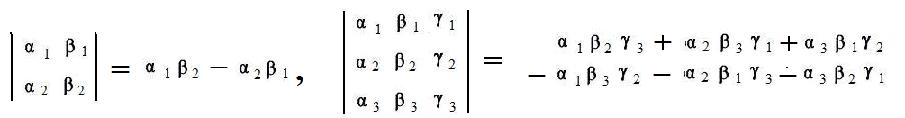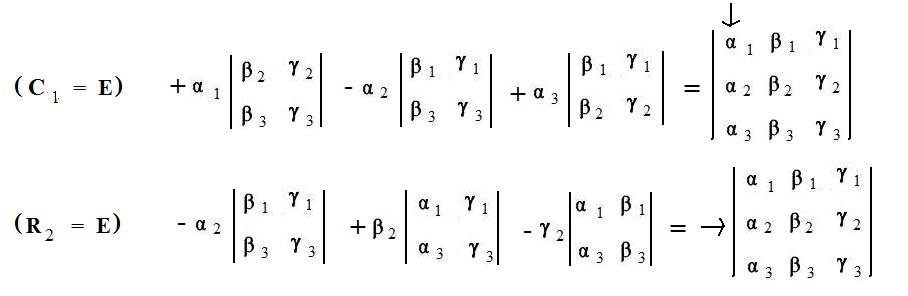Additional Material

Examples of Evaluated Determinants

Let the reader verify the following:

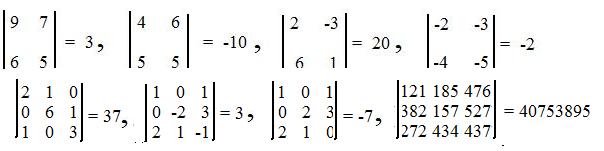Obviously, the value of the last determinant should be verified by computer.

Official Evaluations of Determinants

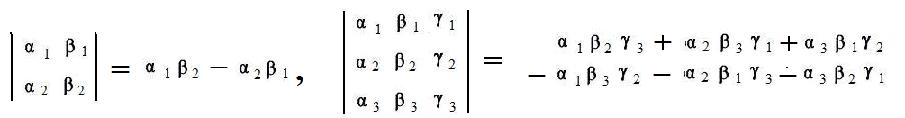The above figure for evaluating the 2x2 determinant shows α, β, with various subscripts which are the two permutations of 1,2. The above figure also shows for evaluating the 3x3 determinant the letters α, β, γ with various subscripts. The subscripts are the six permutations of the first three natural numbers. The even permutations induce plus signs before the terms, while the odd permutations induce negative signs before the terms. This idea can be used by computers to evaluate these and larger determinants. They also can be used to derive some useful properties of determinants of any size.

Let the reader use the cross hatch merthod forevaluating the determinants above to get evaluation expressions that are equivalent to the evaluation expressions also given above. They are equivalent because multiplication and addition of numbers are commutative.

The cross hatch method on an nxn matrix uses 2n diagonals and therefore produces 2n terms. The permutation method produces n! terms. For n=2 or n=3, 2n = n! (2(2) = 2x1 and 2(3) = 3x2x1). But for n>3, 2n < n! (2(4) < 4x3x2x1, and 2(5)< 5x4x3x2x1, etc). Therefore the cross hatch method is not valid for nxn determinants, where n>3.

Evaluation of a 3x3 Determinant by Minors Along Any Row or Any Column

In the previous discussion just above, the official evaluation of the 3x3 determinant is given:
(E) α₁β₂γ₃ + α₂β₃γ₁ + α₃β₁γ₂ -- α₁β₃γ₂ -- α₂β₁γ₃ -- α₃β₂γ₁

Consider now six ways of partially factoring the expression (E):
   (C₁) α₁(β₂γ₃ -- β₃γ₂) -- α₂(β₁γ₃ -- β₃γ₁) + α₃(β₁γ₂ -- β₂γ₁)
   (C₂) -- β₁(α₂γ₃ -- α₃γ₂) + β₂(α₁γ₃ -- α₃γ₁) -- β₃(α₁γ₂ -- α₂γ₁)
   (C₃) γ₁(α₂β₃ -- α₃β₂) -- γ₂(α₁β₃ -- α₃β₁) + γ₃(α₁β₂ -- α₂β₁)
   (R₁) α₁(β₂γ₃ -- β₃γ₂) -- β₁(α₂γ₃ -- α₃γ₂) + γ₁(α₂β₃ -- α₃β₂)
   (R₂) -- α₂(β₁γ₃ -- β₃γ₁) + β₂(α₁γ₃ -- α₃γ₁) -- γ₂(α₁β₃ -- α₃β₁)
   (R₃) α₃(β₁γ₂ -- β₂γ₁) -- β₃(α₁γ₂ -- α₂γ₁) + γ₃(α₁β₂ -- α₂β₁)

Although tedious, simple algebra eliminating parentheses can be used to show that each of the expressions (C₁), (C₂), (C₃), (R₁), (R₂), (R₃) is equal to expression (E), thus producing six algebraic identities

C₁ = E, C₂ = E, C₃ = E, R₁ = E, R₂ = E, R₃ = E,

Each of the expressions in the parentheses in (C₁), (C₂), (C₃), (R₁), (R₂), (R₃) is actually an evaluation of a 2x2 determinant. Replacing parenthetical expressions by its 2x2 determinants in C₁ = E and in R₂ = E produce the equations

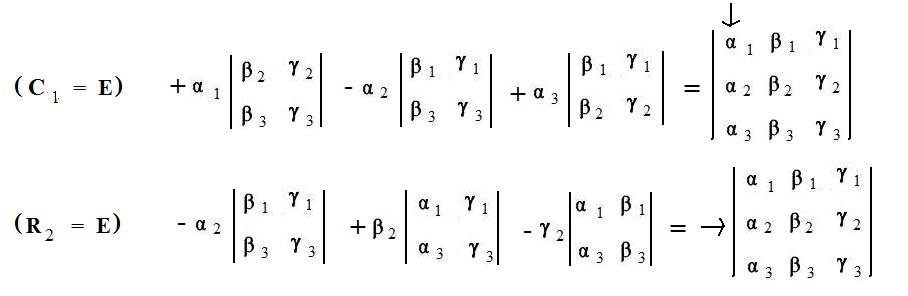
Expansion Using the Wrong Cofactors

Consider the two determinants det M₁ and det M₂:

Columns 1 and 2 are the same in both determinants, but columns 1 and 3 in det M₂ are identical (except for color). Therefore det M₂ = 0 by [1.6a]. Notice the equalities of the following 2x2 determinants: cofactor(γ₁) = cofactor(α₁), cofactor(γ₂) = cofactor(α₂), cofactor(γ₃) = cofactor(α₃) But the expansion by cofactors along the third column of det M₂ is det M₂ = α₁cofactor(α₁) + α₂cofactor(α₂) + α₃cofactor(α₃) Therefore, 0 = α₁cofactor(γ₁) + α₂cofactor(γ₂) + α₃cofactor(γ₃) Consider this last expression as an expansion by cofactors along the first column of det M₁ but using the cofactors along column 3. In a similar way it can be shown that 0 = α₁cofactor(β₁) + α₂cofactor(β₂) + α₃cofactor(β₃)