(*) |u x v| = |u| |v| sin θ if θ is between 0° and 180°.
 From geometry and trigonometry, the right side of the equation (*) is the formula for the area of a parallelogram OUSV as shown in the adjacent figure. Therefore,
From geometry and trigonometry, the right side of the equation (*) is the formula for the area of a parallelogram OUSV as shown in the adjacent figure. Therefore,
From the algebraic identity for real numbers:

Take square roots of both sides, and remembering that the norm |u x v| cannot be negative, to get:
(*) |u x v| = |u| |v| sin θ
if θ is between 0° and 180°.
 From geometry and trigonometry, the right side of the equation (*) is the formula for the area of a parallelogram OUSV as shown in the adjacent figure. Therefore,
From geometry and trigonometry, the right side of the equation (*) is the formula for the area of a parallelogram OUSV as shown in the adjacent figure. Therefore,
[-.-] (Area of a parallelogram) The area of the parallelogram with four vertices origin O and those located by the two position vectors and their sum is equal to the norm of the vector product of those two vectors.
Notation: |u x v| = area of parallelogram OUSB, where diagonal vector OS = u + v.
Example 1. The area of the parallelogram with three vertices (0,0,0), (2,6,8), (2,5,6) is 6 because the norm of the vector product |(2,6,8) x (2,5,6)| = |(-2,-4,4)| = sqrt(4 + 16 + 16 ) = sqrt(36) = 6. The fourth point of the parallelogram is (2,6,8) + (2,5,6) = (4,11,14) but is not needed in the computation.
Notice that the norm |(2,5,6) x (2,6,8)| = 6, also, because the same parallelogram is involved.
Example 2. Show that (1,1,2), (3,7,10), (3,6,8), (5,12,16) are vertices of a parallelogram and find its area. It is easier to handle if the vertices are moved by subtraction of triples, so that one vertex is at the origin. Subtract the first vertex from all four vertices to get (0,0,0), (2,6,8), (2,5,6), (4,11,14). Since the fourth vertex is the sum of the previous two vertices, the vertices belong to a parallelogram (with one vertex at the origin). Therefore, the given vertices before subtraction are those of a congruent figure and is a parallelogram also. Both parallelograms have areas equal to 6.
The statement [-,-] is equivalent to a statement in solid analytic geometry, without the formal use of vectors, only ordered triples:
[-.-] (Area2 of a parallelogram) The square of the area of the parallelogram with vertices at
The geometric interpretation of the norm of the vector product has just been discussed. There remains to determine the direction of the vector product. Let u = (x1, y1, z1), v = (x2, y2,z2) be triples in space. From the algebraic identities for real numbers:
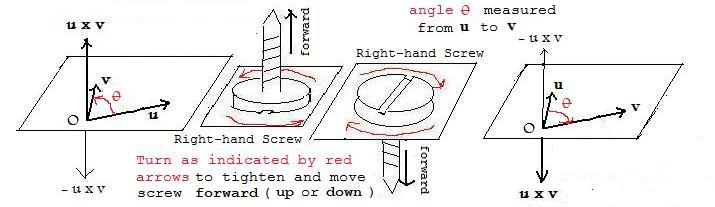
There are exactly two ways that position vector u x v can be perpendicular to this plane, and those ways are vectors pointing in opposite directions. The angle θ is measured from the first vector u mentioned in the vector product u x v to the second vector v in that same vector product. Always choose the angle that is between 0° and 180°.
Most screws are right-hand screws. This means that if the head of the screw is turned to the right, as indicated by the wavy red arrows in the two center figures, the screw will advance forward into the wood. Now place the screw at the origin O so that the face of the head is in the plane of u, v . At the same time, the direction of θ be the same as the wavy red arrows on the head of the screw. Then u x v will point in the direction of the advancing screw when the head is turned (by a screwdriver). This direction is chosen, and not its opposite, so that vector products can be used in vector equations that more simply model some physical phenomena such as induction coils.
If the norm symbols are removed from the left side of equation (*) above, the result is
u x v = |u| |v| sin θ
(angle θ is between 0° and 180°)
This is not a true equation because the left side is a vector, and the right side is a scalar (real number). To make a vector out of the right side, and not change the norm of the right side, attach a unit position vector e to the right side to get:
u x v = |u| |v| sin θ e
Then u x v and e are parallel and point in the same direction. (The directions of u x v and e cannot be determined if u x v is the zero vector. Otherwise, e satisfies the equation u x v = |u x v| e. Divide both sides by |u x v| to get e from u x v.