Additional Material D5

The absolute value of the sum of two real numbers cannot be more than the sum of their absolute values.

Let λ and σ be any real numbers. To prove
   |λ + σ| ≤ |λ| + |σ|.
This is equivalent to
   (λ + σ)² ≤ (|λ| + |σ|)²
Expanding both sides produces:
   λ² + 2λσ + σ² ≤ λ² + 2|λ||σ| + σ²
Cancel like terms on both sides to produce
   λσ ≤ |λ| |σ|
This is true because the left side may be positive or negative (or zero), and the right side is always positive or zero.
The actual proof of |λ + σ| ≤ |λ| + |σ| is obtained by reversing the steps.

Proof that the following definition gives a norm that satisfies the four conditions

The strange norm of any array (x,y) of size 2 is the sum of the absolute values of the coordinates: |(x,y)| = |x| + |y|.
If u = (x₁, y₁) and v = (x₂, y₂), to prove that |u + v| ≤ |u| + |v|.

  (a) |x| + |y| is the sum of two non-negative real number. Hence the sum and u are non-negative real numbers.
  (b) |(x,y)| = 0 <==> |x| + |y|= 0 <==> |x| = 0 and |y| = 0 <==> x = 0 and y = 0 <==> |(x,y)| = |(0,0)| = 0.
  (c) |λ(x,y)| = |λx| + |λy| = |λ| |x| + |λ |y| = |λ| (|x| + |y|) = |λ||(x,y)|.
For part (d) needed is the weak inequality:    the absolute value of the sum of two real numbers ≤ the sum of their absolute values. See discussion above. This means that
   |x₁ + x₂| ≤ |x₁| + |x₂|    and    |y₁ + y₂| ≤ |y₁| + |y₂|
By addition of the inequalities
   |x₁ + x₂| + |y₁ + y₂|    ≤    |x₁| + |y₁| + |x₂| + |y₂|
this means that    |u + v| ≤ |u| + |v|.

The parallelogram law from plane geometry

The sum of the squares of the lengths of two diagonals of a parallelogram is equal to the sum of the squares of all four sides.

Let O,P,S,Q be vertices of a parallelogram (see Fig 1 and Fig 2) Then
   |OS|² + |QP|² = |OP|² + |PS|² + |SQ|² + |QO|²
   |OS|² + |QP|² = |OP|² + |PS|² + |SQ|² + |QO|²
Because opposite sides of a parallelogram have equal lengths, these equations are equivalent to
($)    |OS|² + |QP|² = 2|OP|² + 2|OQ|²
($)    |OS|² + |QP|² = 2|OP|² + 2|OQ|²

Also let θ be the angle at O. So that a genuine parallelogram exists,
       0° < θ < 180°.
There are actually two situations (see Fig 3 and Fig 4):
     0° < θ ≤ 90° and 90° < θ < 180°.

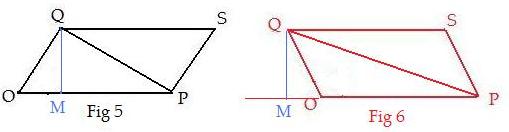
From vertex Q draw diagonal QP and drop a perpendicular down to line OP. Then pairs of right triangles are formed:
   triangle OMQ and PMQ
in both figures Fig 5 and Fig 6. By the Pythagorean theorem
  |OQ|² = |OM|² + |MQ|²,    |QP|² = |PM|² + |MQ|²
in both figures. Subtract the two equations to eliminate |MQ|² to get
(&)    |QP|² − |OQ|² = |PM|² − |OM|²
which is true for both parallelograms.

But now arguments for the black and red parallelograms are different.

In the black parallelogram, eliminate |PM|² by substitution |PM| = |OP| − |OM| whose square is
|PM|² = |OP|² − 2 |OP| |OM| + |OM|²
Inserting the right side of this equation for |PM|² in equation (&) produces
(@) |QP|² = |OP|² + |OQ|² − 2 |OP| |OM|.

In the red parallelogram, eliminate |PM|² by substitution |PM| = |OP| + |OM| to get from (&)
(@) |QP|² = |OP|² + |OQ|² + 2 |OP| |OM|.

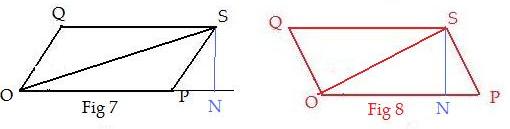
From vertex S draw diagonal OS and drop a perpendicular down to line OP. Then pairs of right triangles are formed:
   triangle ONS and PNS
in both figures Fig7 and Fig 8. By the Pythagorean theorem
  |PS|² = |PN|² + |NS|²,    |OS|² = |ON|² + |NS|²
in both figures. Subtract the two equations to eliminate |NS|² to get
   |OS|² − |PS|² = |ON|² − |PN|²
But |PS| = |OQ| so
(&&)    |OS|² − |OQ|² = |ON|² − |PN|²
which is true for both parallelograms.

But now arguments for the black and red parallelograms are different.

In the black parallelogram, eliminate |ON|² by substitution |ON| = |OP| + |PN| whose square is
|ON|² = |OP|² − 2 |OP| |PN| + |PN|²
Inserting the right side of this equation for |ON|² in equation (&&) produces
(%) |OS|² = OP² + |OQ|² + 2 |OP| |PN|.

In the red parallelogram, eliminate |ON|² by substitution |ON| = |OP| − |PN| to get from (&&)
(%) |OS|² = |OP|² + |OQ|² − 2 |OP| |ON|.

Actually all the black parallelograms are the same. So right triangle OQM and PSN are congruent. Hence |OM| = |PN|.
Similarly, OQM and PSN are congruent. Hence OM = PN. Equations (%) and (%) become
(@@) |OS|² = OP² + |OQ|² + 2 |OP| |OM|.
(@@) |OS|² = OP² + |OQ|² − 2 |OP| |OM|. .

Addition of equations (@) and (@@) and addition of equations (@) and (@@) produce the desired identical equations
|QP|² + |OS|² = 2|OP|² + 2|OQ|²
|QP|² + |OS|² = 2|OP|² + 2|OQ|²

Using position vectors equation ($) becomes |

The Schwarz inequality for any inner product space

The absolute value of the inner product of any pair of vectors in an inner product space cannot be larger than the product of their norms.
Notation: For any vectors u,v in an inner product space, |u⋅v| ≤ |u||v|.

Case I v is the zero vector.
Then |u⋅0| = |u||0| because the equation reduces to 0 = 0.

Case II v ≠ 0
Let λ be the real number equal to a quotient

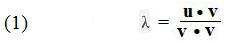
Because squares of real numbers are never negative,

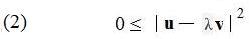
But the right side of (2) becomes:

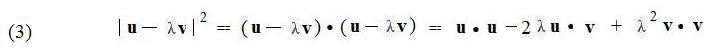
Replace λ in (3) by its equal in (1):

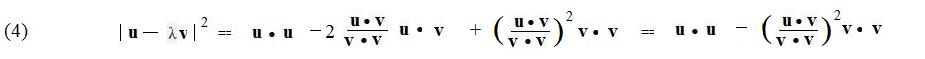
Therefore,

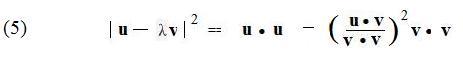
From (2),

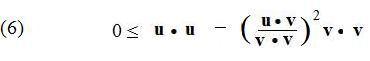
The Schwarz inequality follows from (6) after using some simple algebra and u⋅u = |u|² and v⋅v = |v|²:
|u⋅v| ≤ |u||v|.