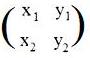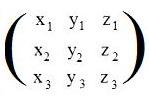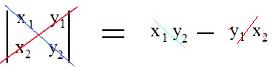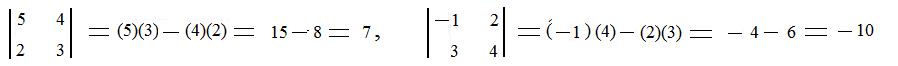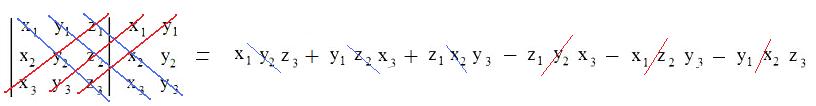Go to other chapters or to other volumes of math
Additional Material for this Chapter
Exercises for this Chapter
Answers to Exercises
Chapter 2: Arrays as Vectors
Section 1: Defining arrays and giving arrays vector properties
In the previous chapter vectors were discussed in the language of geometry. They could be represented as directed line segments in a drawing. Addition and multiplication by real numbers were performed using geometric constructions . That geometric approach indicated the nature of vectors in an intiutive and visible manner, appropriate for a first contact with the subject.
In this section vectors of another type will be discussed. Arrays are more algebraic in nature because they are defined using real numbers in a specific way so that they inherit many properties directly from the real number system and not from drawings. Addition and multiplication by scalars can and will be defined simply and precisely. After that, many of the "laws" that were discussed for geometric vectors will apply equally as well to arrays, and are more easily proven here.
In elementary algebra the plotting of points in the coordinate plane was done using symbols such as (1,2), (3/2,6), (−5,7), ... which locate points in the plane. By choosing the appropriate real numbers for coordinates x and y in (x,y), any point in the plane can be located. Similarly, (x,y,z) can locate any point in space, where x,y,z are real numbers. In this sense, (x,y) and (x,y,z) serve as labels "attached" to points. In addition to x,y,z, other symbols for real numbers will be x,y,z with positive integer subscripts like x1, y1, z1, x2, y2, z2, x3, y3, z3, and any small letters from the Greek alphabet: α, β, γ, δ, ..., λ, σ, ..., ω.
The size of an array is the number of coordinate places in it. The symbols (2,5), (4,−7), (0,0) are examples of arrays of size 2. The symbols (2,5,9), (4,−7,6), (0,0,0) are examples of arrays of size 3. It is obvious how to extend the idea of size to arrays of larger sizes. However, discussions in this section and later will involve mostly arrays of size 2 or 3 because they will be applied to geometries of the plane and space that were discussed in previous sections. Arrays of size 2 are often called ordered pairs. Arrays of size 3 are often called ordered triples. For example, (2,5) and (2,5,9) are an ordered pair and an ordered triple respectively.
Intuitively speaking, an array (_,_,_,...) is a collection of blank places to be filled by real numbers. The number that replaces the left most blank is called the first coordinate of the array. The number replacing the next blank to the right is called the second coordinate of the array. If the size of the array is 3, then the number
replacing the next blank is called the third coordinate of the array. So for the array (8,9,13) the first, second and third coordinates are 8,9, and 13 respectively. In the ordered pair (x,y), x is the first coordinate, and y is the second coordinate. In the ordered triple (x,y,z), x,y,z are the first, second, third coordinates respectively. (Actually, arrays are elements in the setwise products RxR and RxRxR, where R is the set of real numbers.)
Using the term corresponding coordinate(s) it is possible to compare two arrays of the same size. For example, each coordinate in the ordered pair (5,8) is one more than the corresponding coordinate in the ordered pair (4,7). Each coordinate in the ordered triple (10,14,22) is twice the corresponding coordinate in the ordered triple (5,7,11). The idea of corresponding coordinates is so important that a notation involving subscripts will often be used to reflect it. The following are four arrays of sizes 2 and 3:
(x1,y1), (x2,y2),
(x3,y3), (x4,y4)
(x1,y1,z1), (x2,y2,z2), (x3,y3,z3), (x4,y4,z4)
It is convenient to shorten these notations further and combine them into single notations:
array1, array2, array3, array4
with the understanding that within a single discussion array1, array2, array3, array4 all have the same size.
Sometimes, if only one array is involved then array = (x,y) or array = (x,y,z) without subscripts. In particular, zero array = (0,0) or zero array = (0,0,0). It depends upon what size arrays are involved in the discussion. In most discussions unless otherwise noted all arrays are of the same size. Exceptions will show specifically the sizes of arrays involved.
The statements [1.1], [1.2], [1.3] below are basic rules (axioms) for handling arrays.
[1.1] (Equality of arrays) Arrays are equal if and only if they are of the same size and all the corresponding coordinates are equal.
Notation: array1 = array2 if and only if they are of the same size and all the corresponding coordinates are equal.
Notation: (x1,y1) = (x2,y2) if and only if
x1 = x2 and y1 = y2
Notation: (x1,y1,z1) = (x2,y2,z2) if and only if x1 = x2 and y1 = y2 and z1 = z2
The arrays (8+2, 7−6) and (10,1) are equal.
The arrays (4−6, 2+3, 7−7) and (−2,5,0) are equal
The arrays (1,2,3) and (1,2,4) are not equal because the corresponding third coordinates are not equal.
The equality of two arrays of size 2 means 2 equations involving equality between corresponding coordinates.
The equality of two arrays of size 3 means 3 equations involving equality between corresponding coordinates.
This statement [1.1] shows when array1 = array2. It is easy to show that equality of arrays is an equivalence relation:
* reflexive: array = array
* symmetric: if array1 = array2 then array2 = array1
* transitive: if array1 = array2 and array2 = array3 then array1 = array3.
It is trivial to prove that (x,y) = (y,x) if and only if x = y. This shows that the arrangement of numbers in an array is important. Therefore, an array of numbers is different from a simple set or collection of numbers where no order or arrangement is implied, just content.
The familiar addition of numbers may be extended to arrays, that is, how to find the sum array1 + array2:
[1.2] (Addition of arrays) Arrays of the same size may be added by adding corresponding coordinates.
Notation: (x1,y1) + (x2,y2) =
(x1 + x2,y1 + y2)
Notation: (x1,y1,z1) + (x2,y2,z2) =
(x1 + x2,y1 + y2,z1 + z2)
Examples:
(3, 2) + (6, 8) = (3+6, 2+8) = (9, 10)
(4, 3, 1) + (5, 7, 12) = (4+5, 3+7, 1+12) = (9, 10, 12).
It is easy to find (x,y) if (x,y) + (4,7) = (0,10). The answer is (−4,3).
The familiar multiplication of numbers may be extended to arrays. However, the most obvious multiplication of corresponding arrays, by multiplication of corresponding coordinates
(α, β) ⋅ (γ, δ) = (α⋅γ, β⋅δ)
although simple, turns out not to be very useful. The multiplication λarray defined next, is very useful.
[1.3a] (Product of a number and an array) An array may be multiplied by a real number (scalar), by multiplying each coordinate in the array by that number.
Notation: λ(x, y) = (λx, λy)
Notation: λ(x, y, z) = (λx, λy, λz);
2(3,4) = (2⋅3,2⋅4) = (6,8).
3(5,6,7) = (3⋅5,3⋅6,3⋅7) = 15,18,21).
Notice that the same results can be obtained by repeated addition since the multiplying factors 2 and 3 are natural numbers:
2(3,4) = (3,4) + (3,4) = (6,8)
3(5,−6,7) = (5,−6,7) + (5,−6,7) + (5,−6,7) = (15,−18,21).
It is obvious that the product 1array = array:
1(x, y) = (1x,1y) = (x, y)
1(x, y, z) = (1x, 1y, 1z) = (x, y, z)
[1.3b] (Proportional arrays) One array is proportional to a second array if the first array is equal to a product of some real number and the second array.
Notation: array1 is proportional to array2 if and only if there is a real number λ such that array1 = λarray2.
Example: (6,8) is proportional to (3,4) because (6,8) = 2(3,4) where λ = 2.
Example: (10,−12,14) is proportional to (15,−18,21) because (10,−12,14) is 2/3 times (15,−18,21).
Example: (8,3,10) is not proportional to (1,2,3).
[1.3c] (Positively proportional arrays) One array is positively proportional to a second array if the first array is equal to a product of some positive real number and the second array.
Notation: array1 is positively proportional to array2 if and only if there is a positive number λ such that array1 = λarray2.
[1.3d] (Negatively proportional arrays) One array is negatively proportional to a second array if the first array is equal to a product of some negative real number and the second array.
Notation: array1 is positively proportional to array2 if and only if there is a negative number λ such that array1 = λarray2.
Note: Being proportional among non-zero arrays of the same size is an equivalence relation.
***
From the basic properties stated in [1.1], [1.2], [1.3a] and the familiar properties of simple numbers, the following statements about arrays and real numbers are easily proven.
[1.4] (Addition is commutative) Two arrays of the same size may be added in either order.
Notation: array1 + array2 = array2 + array1
The proof is based on the commutativity of real numbers and the equality of arrays:
x1 + x2 = x2 + x1 ,
y1 + y2 = y2 + y1
(and for arrays of size 3) z1 + z2 = z2 + z1
[1.5] (Addition is associative) For the sum of three arrays of the same size, either addition may be done first.
Notation: (array1 + array2) + array3 = array1 + (array2 + array3)
The proof is based on the associativity of real numbers and the equality of arrays:
(x1 + x2) + x3 = x1 + (x2 + x3) ,
(y1 + y2) + y3 = y1 + (y2 + y3) ,
(and for arrays of size 3)
(z1 + z2) + z3 = z1 + (z2 + z3)
The addition inside the parentheses is done before the addition outside the parentheses.
[1.6] (Additive identity) The zero array with all coordinates equal to zero is the additive identity.
Notation: array + zero array = array.
Proof is based on the fact that 0 is the additive identity for real numbers:
(x, y) + (0,0) = (x + 0, y + 0) = (x, y), (x, y, z) + (0, 0, 0) = (x + 0, y + 0, z + 0) = (x, y, z)
Notice that the product 0array = the zero array.
[1.7] (Additive inverse) Every array has an additive inverse obtained by negating all of the coordinates.
Notation: (−x, −y) is the additive inverse of (x,y). − (x,y) will denote the additive inverse of (x,y).
Notation: (−x, −y, −z) is the additive inverse of (x,y,z). − (x,y,z) will denote the additive inverse of (x,y,z).
Notation: − array will denote the additive inverse of array.
Simple computations show that (x,y) + (−x, −y) = (0,0) and that (x,y,z) + (−x, −y, −z) = (0,0,0). Therefore, array + (− array) = zero array.
The expression − array is also called the negative of the expression array.
Notice that the product (−1)array = the negative of array = additive inverse of array.
[1.8a] (Formal subtraction) To subtract a second array from a first array of the same size, add the negative of the second array to the first array.
Notation: array1 − array2 = array1 + (− array2).
An equivalent but more useful fact is the following:
[1.8b] (Subtraction) One array may be subtracted from another array of the same size by subtracting the corresponding oordinates in that order.
Notation: (x1, y1) − (x2, y2) =
(x1 − x2, y1 − y2)
Notation: (x1, y1, z1) − (x2, y2, z2) =
(x1 − x2, y1 − y2, z1 − z2)
Proof is based on the definition of subtraction of real numbers and equality of arrays:
x1 − x2 = x1 + ( − x2), y1 − y2 = y1 + ( − y2), (and for arrays of size 3) z1 − z2 = z1 + ( − z2)
There are two distributive laws involving products of real numbers and arrays.
[1.9] (Right distributive) The product of the sum of two real numbers and an array is equal to the sum of the products of each real number and the array.
Notation: (λ + σ)array = λarray + σarray
The proof of this law is based upon the fact that (λ + σ)x = λx + σx similarly for y and z.
[1.10] (Left distributive) The product of a real number and the sum of two arrays of the same size is equal to the sum of the products of that real number and each of the arrays.
Notation: λ(array1 + array2) = λarray1 + λarray2.
The proof of this law is based upon the fact that λ(x1 + x2) = λx1 + λx2 similarly for y1, y2, z1, z2 (if size = 3).
Of course, all arrays in [1.10] are of the same size.
[1.11] (Proportional arrays) One array is proportional to a second array if and only if there is a real number such that the first array is equal to the product of that real number and the second array. The real number is called the proportionality factor.
Notation: array1 is proportional to array2 if and only if
array1 = λarray2.
Example (6,8,10) is proportional to (3,4,5) because (6,8,10) = 2(3,4,5). The number 2 is the proportionality factor.
Section 2: Associating arrays and position vectors
The reader may have noticed the similiarity in the discussions about geometric vectors and about arrays. This similarity suggests a close association between them. Intuitively speaking, they do the same things with different objects. The discussion of the association starts with the assignment of arrays to points. If the universe is a plane then any point in the plane may be assigned a label such as P (called a name) or assigned a label such as an array (x,y) of size 2. If the universe is space then any point in space may be assigned a name such as P or assigned a label such as an array (x,y,z) of size 3. The symbol P(x,y) or P(x,y,z) means that some point has been assigned both a name P and an array label.
Whenever position vectors are discussed some fixed origin O will be assumed. Then for any points P, Q, R the position vectors
p = OP, q = OQ, r = OR
will exist.
Examples: P(4,5) is a point in a plane with two attached labels, P and (4,5). Q(7,−4,6) is a point in space with two attached labels, Q and (7,−4,6). in space. Then position vector p and array (4,5) locate the same point P in a plane. Position vector q and array (7,−4,6) locate the same point in space.
[2.1] (Equivalent position vectors and arrays) A position vector and an array are equivalent if and only if they locate the same point.
Notation: p and (x,y) are equivalent if and only if p and (x,y) locate the same point in a plane.
Notation: q and (x,y,z) are equivalent if and only if p and (x,y,z) locate the same point in space.
The symbol P(x,y) means that p and (x,y) are equivalent. Similarly, the symbol Q(x,y,z) means that q and (x,y,z) are equivalent. It is somewhat awkward to say that p and (x,y) are equivalent. Instead the notation p = (x,y) will be used to indicate equivalence. Similarly, q = (x,y,z) will be used for equivalence.
This equivalence is actually a one-to-one correspondence between position vectors and arrays. The following fact shows that the two addition operations, one for position vectors and one for arrays, also correspond. (Therefore, the one-to-one correspondence has the nature of an additive isomorphism between position vectors and arrays for each universe, a plane and space.)
The next two statements [2.2] and [2.3] allow computation to handle some of the situations of vectors. However, it is helpful for understanding to remember the corresponding geometric interpretations.
[2.2] (Isomorphism between position vectors and arrays) If two position vectors and two arrays locate the same two points respectively, then the sum of the position vectors and the sum of the arrays locate the same point.
Notation: if both p and an array1 locate point P, and both q and array2 locate point Q, then their sums
p + q and array1 + array2
locate the same point.
Click here to see the discussion supporting [2.2].
[2.3] (Corresponding products of scalars and vectors) If a position vector and an array locate the same point, then the product of any real number and the position vector and the product of the same real number and the array locate the same point.
Notation: if both p and an array locate point P, and λ is any real number, then both λp and λarray locate the same point.
Click here to see the discussion supporting this statement.
Examples: 0 = (0,0). If p = (4,5) and q = (6,8) then p + q = (10,13), 3p = (12,15), q − p = (2,3).
Examples: If A(3,7) and B(9,4), find the coordinates of the point P(x,y) of trisection of AB, nearest A. 3p = 2a + b. Then 3(x,y) = 2(3,7) + (9,4) = (6,14) + (9,4) = (15,18). Therefore, (3x,3y) = (15,18). Hence (x,y) = (5,6). p = (5,6). P(5,6) is the desired point of trisection nearest A.
Because of [2.1], [2.2], [2.3] the statements about position vectors given in the previous chapter are supported by the proofs of corresponding statements about arrays given in the previous section.
As a result of [2.3] parallel position vectors correspond to proportional arrays. If the proportionality factor is positive, then the arrays have the same direction. If negative, then they have opposite direction. In any case the parallel position vectors and the proportional arrays locate poiints on a line through the origin.
(8,6) has the same direction as (4,3), but (6,12) has the opposite direction as (−1,−2). Notice that the origin is not between (8,6) and (4,3). But the origin is between (6,12) and (−1,−2).
* * *
The following statement comes from elementary geometry:
(*) If two segments have a common end point, and a common mid point, then the two segments coincide.
Some discussions below make use of the mid point formula from elementary analytic geometry.
Both the position vector and the array have additive inverses: −p and − (x,y) = (−x,−y).
[2.11] (Corresponding additive inverses) If position vector and an array locate the same point, then the additive inverse of the position vector and the additive inverse of the array locate the same point.
Notation: if p and (x,y) locate the same point P, then − p and − (x,y) locate the same point.
Notation: if p and (x,y,z) locate the same point P, then − p and − (x,y,z) locate the same point.
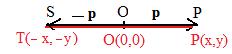 In the adjacent figure O is the origin P is the point located by position vector p. The vector − p is another position vector that points in the opposite direction and locates some point, say S. O(0,0) is the same origin as O, and P(x,y) is the same point P. The additive inverse (−x,−y) of array (x,y) locates some point, say T. The purpose of this discussion is to show that S = T. Since (−x,−y) + (x,y) = (0,0) the mid point formula (**) shows that (0,0) locates the mid point of segment TP. The segments SP and TP must coincide by (*) because they have a common mid point O and O and a common end point P and P. Therefore S = T; the inverse of p locates the same point as the inverse of (x,y).
In the adjacent figure O is the origin P is the point located by position vector p. The vector − p is another position vector that points in the opposite direction and locates some point, say S. O(0,0) is the same origin as O, and P(x,y) is the same point P. The additive inverse (−x,−y) of array (x,y) locates some point, say T. The purpose of this discussion is to show that S = T. Since (−x,−y) + (x,y) = (0,0) the mid point formula (**) shows that (0,0) locates the mid point of segment TP. The segments SP and TP must coincide by (*) because they have a common mid point O and O and a common end point P and P. Therefore S = T; the inverse of p locates the same point as the inverse of (x,y).
The arrays (x,y), (0,0), (−x,−y) of size 2 may be replaced by (x,y,z), (0,0,0), (−x,−y,−z) to obtain a similar discussion of vectors and points in space and arrays of size 3.
Section 3: Determinants of order 2 and 3
In this section square matrices of sizes 2x2 abnd 3x3 are introduced. Then most attention will be directed at determinants of them. More general discussions are given in the volume E on Linear Transformations and Matrices.
[3.1a] (Forming a 2x2 matrix) An ordered collection of two arrays of length two may form a 2x2 matrix by placing the second array under the first array.
Notation: The matrix of the ordered collection (x1, y1) and (x2, y2) is
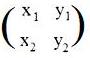
Every 2x2 matrix has 4 numbers in it.
[3.1b] (Forming a 3x3 matrix) An ordered collection of three arrays of length three may form a 3x3 matrix by placing the second array under the first and the third array under the second.
Notation: The matrix of the ordered collection (x1, y1, z1),
(x2, y2, z2), and (x3, y3, z3) is:
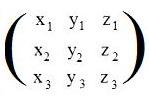
Any 3x3 matrix has 9 numbers in it.
Although the discussions can be made to apply to arrays and square matrices of larger sizes in obvious generalizations, the discussions here will involve only square matrices of sizes 2x2 and 3x3.
To each square matrix is associated a real number, called the determinant value or simply determinant of the matrix. The process of calculating this value is called the evaluation of the determinant. It usually involves a definite pattern of arithmetic operations of sums of products and differences of products involving all the numbers in the matrix.
In these discussions the matrices are always square. Therefore they have diagonals slanted \ and /, that is, going from upper left to the lower right (slanted backward) and going from the upper right to the lower left (slanted forward). The first diagonal forms a product ready for addition, and the second (diagonal) forms a product ready for subtraction.
[3.2a] (Evaluation of a 2x2 determinant) To find the value (a real number) of a 2x2 determinant, calculate the product of the numbers along each of the two diagonals. Then perform a calculation: product along the blue diagonal minus the product of the numbers along the red diagonal.
Notation:
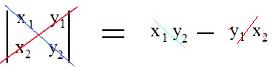
Example1:
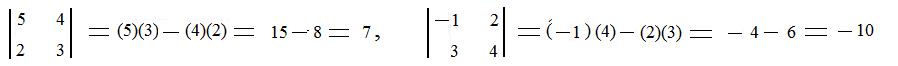
Example2: The determinant value of the ordered collection (4, 5) and (6, 7)} is −2 because

[3.2b] (Evaluation of a 3x3 determinant) To find the value of a 3x3 determinant, copy the first two columns to the right of the determinant, then calculate the sum of the products of the numbers along each of the three blue. From that sum subtract the sum of the products along the three red diagonals:
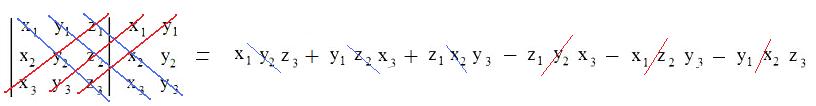 Example: the value of the determinant of the ordered collection (1,2,3), (4,5,6), (7,8,9) of triples is 0 because
Example: the value of the determinant of the ordered collection (1,2,3), (4,5,6), (7,8,9) of triples is 0 because

It is often significant if the determinant value of a square matrix is zero, positive or negative.
[3.3] (Singular collections) A collection of arrays is singular if the value of its determinant is 0. A non-singular collection has a determinant with a non-zero value.
All of the ordered collections (5,4), (2,3), (−1,2), (3,4), (4,5), (6,7) are non-singular (see examples after [3.2a]). The ordered collection (1,2,3), (4,5,6), (7,8,9) is singular (see example after [3.2b]).
Singular and non-singular will be given algebraic interpretations and play an important role in the volume on Linear Transformations and Matrices. They will be given geometric interpretations in later chapters.
[3.4] (Orientation) If the value of a determinant of an ordered collection of arrays is a positive number then the ordered collection has positive orientation. If the value of a determinant of an ordered collection of arrays is a negative number then the ordered collection has negative orientation.
The orientation of a singular collection is not defined.
The ordered pairs in the ordered collection (1,0), (0,1) are listed in their natural order. The collection has positive orientation. The ordered triples in the ordered collection (1,0,0, (0,1,0), (0,0,1)} are listed in their natural order. The collection also has positive orientation.
But the ordered collection (0,1), (1,0) and the ordered collection (0,0,1), (0,1,0), (1,0,0)} have negative orientation. It is obvious that the order in which arrays are listed affects the orientation of the collection. (See [3.5d] below.) That is why the collections are called ordered.
[3.5] (Values of determinants) Some useful properties of determinants.
(a) If the zero vector is in the ordered collection then the determinant value of that collection is zero. (If any row has all zeros then the value of the determinant is zero.)
(b) If two arrays in an ordered collection are equal then the determinant value of that collection is zero. (If two rows are identical then the value of the determinant is zero.)
(c) If two of the arrays in an ordered collection are proportional then the value determinant value of that collection is zero. (If one row is proportional to another row then the value of the determinant is zero.)
(d) If two arrays in an ordered collection are interchanged then determinant value of that collection is changed - from positive to negative or from negative to positive. (If two rows are interchanged then the value of the determinant is negated (changed from positive to negative or changed from negative to positive)).
(e) If any array in an ordered collection is multiplied by a real number, then the determinant value of that collection is multiplied by the same real number. (If every number in any single row is multiplied by a real number, the the value of the determinant is multiplied by that same real number.)
Click here to see proofs of [3.5].
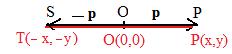 In the adjacent figure O is the origin P is the point located by position vector p. The vector − p is another position vector that points in the opposite direction and locates some point, say S. O(0,0) is the same origin as O, and P(x,y) is the same point P. The additive inverse (−x,−y) of array (x,y) locates some point, say T. The purpose of this discussion is to show that S = T. Since (−x,−y) + (x,y) = (0,0) the mid point formula (**) shows that (0,0) locates the mid point of segment TP. The segments SP and TP must coincide by (*) because they have a common mid point O and O and a common end point P and P. Therefore S = T; the inverse of p locates the same point as the inverse of (x,y).
In the adjacent figure O is the origin P is the point located by position vector p. The vector − p is another position vector that points in the opposite direction and locates some point, say S. O(0,0) is the same origin as O, and P(x,y) is the same point P. The additive inverse (−x,−y) of array (x,y) locates some point, say T. The purpose of this discussion is to show that S = T. Since (−x,−y) + (x,y) = (0,0) the mid point formula (**) shows that (0,0) locates the mid point of segment TP. The segments SP and TP must coincide by (*) because they have a common mid point O and O and a common end point P and P. Therefore S = T; the inverse of p locates the same point as the inverse of (x,y).