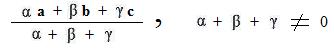Return to main text in Chapter 1
Vectors locating points in planes and space
The discussion for planes is similar to the discussion for lines. It requires two points to determine a (straight) line, but the points cannot coincide. It requires three points to determine a plane, but the points cannot lie on the same line (not collinear). Later the following statement will be examined: it requires four points to determine space, but no three of them can lie in the same plane (not coplanar).
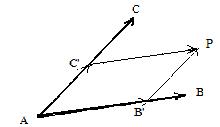Let A and B be any two distinct points. A point P lies on the line AB if an only if there is a real number λ satisfhying the vector equation AP = λAB. Let A, B and C be any distinct points, such that they do not all lie on the same line. (The origin O is not necessarily in plane ABC.) Then point P lies in the plane ABC determined by the three points if and only if there exist real numbers λ and σ satisfying the vector equation
(*) AP = λAB + σAC.
This is an addition of vectors, and therefore involves a involves a parallelogram. Let B' and C' be points on lines AB and AC such that AB' = λAB and AC' = σAC. Then AB'PC' is an addition parallelogram. See adjacent figure.
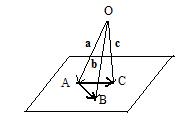The figure to the right shows origin O not in the plane ABC, but somewhere else in space. In the equation (*) above suppose λ = 1/3 and σ = 4/9 so that
(**) AP = (1/3)AB + (4/9)AC.
However, each of the points A,B,C,P have position vectors (in space). Each of the vectors AB, AC, AP in the equation (**) may be replaced by the differences of those position vectors to produce the equation
(***) p -- a = (1/3)(b - a) + (4/9)(c -- a)
Multiply both sides by 9 to clear fractions and solve for 9p:
(****) 9p = 2a + 3b + 4c
Notice that λ = 3/9 so that the fractions of λ and σ have the same denominator 9. So with no loss of generality, let λ = β/μ &nbasp σ = γ/μ . Then (*) becomes:
(##) AP = (β/μ)AB + (γ/μ)AC.
Replace each of the vectors AB, AC, AP by the differences of position vectors to get
(###) p -- a = (β/μ)(b - a) + (γ/μ)(c -- a)
Finally, multiply both sides by μ to clear fractions and solve for μp:
(####) μp = (μ -- β -- γ)a + βb + γc
Now let α = μ -- β -- γ. This means that μ = α + β + γ Replacing (μ -- β -- γ) by α and μ by (α + β + γ) the following is the result:
(&) (α + β + γ)p = αa + βb + γc
Actually, α, β, γ need not be integers, but may be any real numbers not all zeros. If the sum
α + β + γ = 0
then it can be shown that one of the three points A,B,C is on the line through the other two or all three points coincide. If the sum is not zero, then in (&) solve for p to get the fraction
(&&)
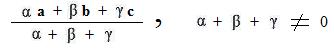
which represents a position vector locating a point in the plane ABC. By letting the real number coefficients α, β and γ range all over the real number scale, but not omitting those values that let their sum α + β + γ be zero, the position vector (&&) will cover all points in the plane ABC.
If the (non-zero) denominator is divided into each of the coefficients of the lincomb in the numerator, then the results give the barycentric coordinates of the point. For example, since the centroid is located by the position vector g in the equation
3g = a + b + c
the barycentric coordinates the centroid point G of a triangle ABC are 1/3, 1/3, 1/3 (solve for g first). And the barycentric coordinates of the vertices A, B, C themselves are respectively 1,0,0 0 1 0 0 0 1. The sum of all barycentric coordinates for any point must be 1.