Relations and Functions

Go to other chapters or to other books of math
Additional Material for this Chapter
Exercises for this Chapter

Volume C Chapter 1
Relations and Functions

Section 1 Introduction to Relations

Among some the people on the earth there are relations between them. Expressions like
"is a parent of", "is married to", "is taller than", "has more money than"

are relations between two people.

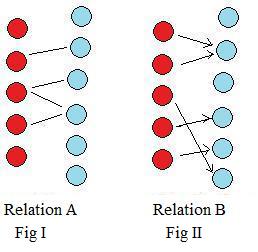
The idea of relations may be extended to objects. In the adjacent figures, the five red circles represent boats, and the six blue circles represent poles on a dock. Some or all of the boats are tied to some of the poles. In Fig I, some boats are tied to poles, and two boats use their own anchors.
In Fig II, all of the boats are tied to some poles.

These ropes relate boats to poles. The open statement

x is tied to y expresses this relation. Also used is the tilda to mean "is related to": x ~ y The statement about a relation may be true or false. Not every boat is tied to every pole for either relation A or B.

Label the boats with the numbers 1, 2, 3, 4, 5 from top to bottom. Label the poles 1, 2, 3, 4, 5, 6 also from top to bottom. Then the following are all the true relations for A (Fig III): 2 ~ 2, 3 ~ 3, 3 ~ 4, 4 ~ 4 and all the true relations for B (Fig IV): 1 ~ 2, 2 ~ 2, 3 ~ 6, 4 ~ 4, 5 ~ 5

It is customary to be concerned with only the true relations. Unless mentioned otherwise, b ~ c means that object b is truly related to object c.
The relations exist between objects in two sets, BOATS = {1,2,3,4,5} and POLES = {1,2,3,4,5,6}. No confusion exists if it is said that the relations exist between the sets BOATS and POLES themselves.

-----

The following is a technical definition of a relation between two sets:

[1.1] (Relation between two sets) A relation between two sets is a subset of their Cartesian product.
Notation: x ~ y if and only if the ordered pair (x,y) is in that subset.

For a discussion of Cartesian products click here.

It is possible to produce a relation from a given relation.

[1.2] (Reverse relations) For any relation between sets U and V, the reverse relation is between V and U and is obtained by reversing every relation x ~ y between objects x in U, y in V, to get y ~ x. which is called the reverse relation of x ~ y.

For the relation in FIg IV,
given relation: 1 ~ 2, 2 ~ 2, 3 ~ 6, 4 ~ 4, 5 ~ 5
reverse relation: 2 ~ 1, 2 ~ 2, 4 ~ 4, 5 ~ 5, 6 ~ 3
Clearly the reverse relation is different from the given relation.
The truth values of relation of x ~ y and y ~ x may be the same or may be different. If ~ means "is tied to" then all of the above relations are true. The reverse of "John is the father of Bill" is "Bill is the father of John". Obviously, both relations cannot be true.

[1.3] (Symmetric relations) A relation is symmetric if every relation between objects and its reverse have the same truth value.
Notation: Relation ~ is symmetric if and only if x ~ y always implies y ~ x.

In the above example, a boat "is tied to" a pole always implies that the pole "is tied to" the boat. So "is tied to" is a symmetric relation. Also symmetric are the following relations:
"is a brother of", "is equal to", "has the same color as", "is in the same subset as", "is parallel to"
Not symmetric relations are "is father of", "is less than", "is taller than".

The idea of linking abstract objects together is discussed in graph theory. There is a volume on this subject in the collection of volumes.

Section 2: Equivalence relations

Some useful relations involve only one set, that is, a relation between a set U and itself: U ~ U. Then the relation is said to be a relation on a set U.

Recall from Volume I the idea of equivalence.
Two objects are equivalent if they have the same property and all other distinguishing properties are ignored.
Suppose a bag contains 5 apples, 4 oranges, 3 peaches, 3 plums, all in excellent condition. All the apples are equivalent, so are equivalent the oranges, so are the peaches and so are the plums. The equivalence ignores different weights, sizes, number of seeds, etc. Let x,y,z denote the fruit in the bag. Then

x is equivalent to y if and only if x,y are the same type of fruit Trivially, if x and y are equivalent (same fruit) then y and x are equivalent. Also trivial, if x and y are equivalent, and y and z are equivalent, then all three x,y,z are equivalent. Therefore x and z are equivalent. Also allow any fruit to be equivalent to itself. (But notice that not all pairs of fruit in the bag are equivalent: apples, oranges, peaches and pears are different.) These ideas lead to the following definition:

[2.1] (Equivalence relations) A relation ~ on a set U is an equivalence relation if and only if it satisfies the following three conditions:
  (a) the relation is reflexive: for all objects x in U, x ~ x;
  (b) the relation is symmetric: for all objects x,y in U, if x ~ y then y ~ x;
  (c) the relation is transitive: for all objects x,y,z in U, if x ~ y and y ~ z then x ~ z.

Example [2.1a] The simple relation ~ on N₅ = {1,2,3,4,5} defined by only three relations between objects:

2 ~ 3, 3 ~ 4, 1 ~ 5 violates all three conditions.
To satisfy (a) the relations 1 ~ 1, 2 ~ 2, 3 ~ 3, 4 ~ 4, 5 ~ 5 are needed.
To satisfy (b) the relations 3 ~ 2, 4 ~ 3, 5 ~ 1 are needed.
To satisfy (c) the relation 2 ~ 4 is needed, because of the first two given relations 2 ~ 3, 3 ~ 4.

Example [2.1b] For the fruit in the bag mentioned above, the relation x ~ y if and only if x,y are the same type of fruit is an equivalence relation.

Example [2.1c] Color all the numbers in N₁₂ with three colors: (#) {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12} Then define the relation as: x ~ y if and only if x,y have the same color Then all three conditions (a), (b), (c) are easily verified.

The following are equivalence relations (allow people and objects to be related to themselves):
"has the same color as", "is a brother of", "is equal to", "is in the same subset as", "is congruent to", "is similar to", "is parallel to" [this is contrary to the definition in plane geometry that parallel lines must be distinct]
Not equivalence relations are: "is father of", "is less than", "is taller than", "is not equal to".

An important feature of equivalence relations is the distinctive gathering of equivalent objects. In example [2.1b] all the apples can be taken out of the bag and put in a separate bag. Similarly the oranges can go into a separate bag, the peaches into a separate bag and the plums into a separate bag. The smaller bags contain disjoint collections of fruit and together the contents of all the four smaller bags contain all the fruit that was in the original bigger bag.
Similarly, in example [2.1c] all the red numbers form a subset, all the green numbers form a subset, and all the blue numbers form a subset. The three subsets together contain all twelve numbers, and no number is in two different subsets.
The following statement reveals the importance of equivalence relations.

[2.2] (Equivalence classes) Let there be an equivalence relation on a set U. If all the objects are gathered into collections of equivalent objects then those collections form a partition of the set. The collections are called equivalence classes.

For a discussion supporting [2.2] click here.

Section 3: Introduction to Functions

Another important relation is discussed in this section. Two distinguishing properties are given here:

[3.1] (Functions) A function from a first set to a second set is a relation between the two sets satisfying the following conditions:
(a) every object in the first set is involved in the relation;
(b) no object in the first set is related to more than one object in the second set.
Notation: f: U → V means that f is a function from set U to set V.

Example [3.1a]
The adjacent figures show again two relations between boats and poles. In both figures, the collection of boats is the first set and the collection of poles is the second set. Relation A in Fig III is not a function because it violates both conditions. It violates (a) because boat 1 and boat 5 are not involved in the relation. It violates (b) because boat 3 is related (tied) to two different objects in the second set, namely pole 3 and pole 4.

On the other hand, Relation B in Fig IV is a function because it satisfies both conditions. Every boat is involved (tied up), and no boat is related (tied) to two different poles.

Notice that boat 1 and boat 2 in Fig IV are related (tied) to the same pole 2. A function is allowed to relate different objects in the first set to a single object in the second set (but a function must not relate a single object in the first set to different objects in the second set). Also notice that not all the poles are involved (used). A function need not involve all objects in the second set (but it must involve all objects in the first set).
In fact, it is impossible for all five boats to be tied to all six poles and not violate condition (b).

Example [3.1b]
This time let the first and second sets be the integers J. Relate each integer to its square: x ~ x². All the integers x are involved, so condition (a) is satisfied. Every integer x has only one square x², so condition (b) is satisfied. So squaring each integer is a function. Even though both 3 ~ 9 and -3 ~ 9, that is permitted for a function.

Almost never is the notation ~ used for a function. Sometimes an arrow is used, pointing from objects in the first set to objects in the second set. For the function in Fig IV,

1 → 2, 2 → 2, 3 → 6, 4 → 4, 5 → 5 Most often functions have names. In these discussions the names f, g, or h are often used. (But some branches of mathematics have their own names.) Let f be the name of the function given in Fig IV. Then the notation f(1) = 2, f(2) = 2, f(3) = 6, f(4) = 4, f(5) = 5 shows how f relates boat numbers to pole numbers in Fig IV.
The notation f( ), g( ), h( ) is called function notation.

Example [3.1c]
Let J = set of all integers. The function g: J → J that triples every integer can be defined by writing

g(x) = 3x for every x in J Then g(2) = 6, because g(2) = 3(2). Similarly, g(5) = 15, g(-6) = -18.
If x in g(x) is replaced by something, then every x in g(x) = .... is replaced by that same thing: g(b) = 3b.

If f: U → V is the function that relates object x in the first set U with object y in the second set V then y = f(x) expresses this relation. This also allows the plotting of points (x,y) that satisfy this equation. For real numbers , and y, if

y = f(x) = 2x then y = f(1) = 2, so (x,y) = (1,2) is a point on the graph of f. Similarly, y = f(-3) = -6, so (-3,-6) is a point on the graph of f. All the points (x,y) satisfying y = f(x) = 2x form a straight line of slope 2, and passing through the origin (0,0).

If y = f(x) then f relates x to y. y is then called the image of x. In Fig IV above,

the image of 1 is 2, the image of 2 is 2, the image of 3 is 6, the image of 4 is 4, the image of 5 is 5, If more than one function is involved, add the phrase "under f, under g, under h". If f(x) = 2x, then 6 is the image of 3 under f because f(3) = 6. Similarly, the images of 4, 10, -15 are 8,20,-30 respectively.

A function from a first set to a second set involves all objects of the first set. The first set is also called the domain of the function. In Fig IV, the domain of the function is

{1,2,3,4,5} The images of all the objects in the first set or domain form a subset of the second set< and this subset is called the range of the function. The range of the function in Fig IV = {2,4,5,6} Notice that the range is not all of the second set: second set (all poles) = {1,2,3,4,5,6} because 1 and 3 are not images of any objects in the domain (see Fig IV).

The adjacent figure shows a function f from a first set (red rectangle) to a second set (interior of the larger black rectangle). The solid blue rectangle is the range of f. What is outside the rectangle is not in the range of f. So part of the second set is not in the range of f. That part contains no images of objects in the domain of f. If y is an object in that part then it is impossible to find an x such that f(x) = y. The range need not be all of the second set. But sometimes it is, as discussed in the next section, Special Functions.

These discussions use either of two methods to show a function carrying objects onto objects: verbal notation, arrow notation, and function notation involving objects x and y.
verbal notation    function f carries x onto y.
arrow notation    f:    x → y
function notation    f(x) = y.

The arrow notation used in Fig IV shows what objects in the domain are related to what objects in the range. The arrows always point to the images. For this reason, often it is said that the function carries an object (in the domain) onto an object (in the range). In Fig IV,
the function carries 3 onto 6.
In arrow notation: 3 → 6.
In function notation: f(3) = 6, where the f is tne name of the relation of boat tied to pole
The first two notations are useful if the name of the function is not needed. The last notation is sometimes useful if more than one function is involved.

Consider a function f: N₁₀ → N₂₅ defined by

1 → 5, 2 → 6, 3 → 8, 4 → 8, 5 → 11, 6 → 11, 7 → 16, 8 → 19, 9 → 21, 10 → 21. which means that f(1)=5, f(2)=6, ..., f(10)=21
Now {3,4,5,6,7,8} is a subset of N₁₀. The images of every object in that subset are 8,11,16,19,21. These form a subset of N₂₅. So f carries every object in the first subset onto the second subset: {3,4,5,6,8} → {8,11,19} Notice that every object in the second subset is the image of some object in the first subset, that is: {8,11,19} = {f(3),f(5),f(8)}

[3.2a] ("onto" subsets) A function carries a first set to a second set. It carries a subset of the first set onto a subset of the second set if and only if
the image of every object in the first subset is in the second subset and every object in the second subset is the image of some object in the first subset.
Notation1: let f: U → V be a function. Let A be a subset of U and B be a subset of V. f carries A onto B if and only if
(i) f(x) is in B for every x in A;
(ii)for every y in B there is an x in A such that f(x) = y.
Notation2: f(A) = B.

Recall that a subset may be the whole set. Then condition (i) is not needed since the first set is the entire domain of the function.

[3.2b] ("onto" functions) A function carries a first set onto a second set if and only if every object in the second set is the image of some object in the first set.
Notation1: f:U → V is a function from U onto V if and only if every object in V is the image of some object in U. Notation2: f(U) = V.

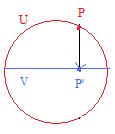
In the adjacent figure a U =circle (first set) and its V = diameter (second set) are given. For any point P in the circle drop a perpendicular line and let point P' be the intersection with the diameter. Then the function that carries P onto P' carries the circle onto the diameter. Every point on the diameter is the image of a point on the circle, usually two points on the circle.

-----

The following gives the conditions that two functions be equal:

[3.3] (Equality of functions) Two functions from a first set to a second set are equal if and only if they satisfy the following conditions
(a) they have the same domains;
(b) they carry each object in that domain onto the same object in the second set.
Notation: f = g if and only if (a) domain of f = domain of g, and (b) for every x in the domain, f(x) = g(x).

Intuitively speaking, equal functions do the same thing to each object in the common domain.
There is a redundance in [3.3]. If the two functions carry the same first set (into a second set), then the domains are already equal. But condition (a) is given to make identifying equal functions easier.

Example: if the first and second sets are the integers J, and f and g carry J into J, defined by

f(x) = 2(x + 1) and g(x) = 2x + 2 for every integer x It is obvious that f and g satisfy both conditions of (a) and (b) of [3.2] because of an identity from elementary algebra f(x) = 2(x + 1) = 2x + 2 = g(x) Therefore, f and g carry each x in the domain onto the same image f(x) = g(x).

Notice that for equality, f and g must carry every object x in their common domaim onto the same object in the second set f(x) = g(x), not just some of the objects in the common domain x, and some other objects x' in the common domain onto different objects in the second set, f(x') not equal to g(x').

-----

Even though the phrase that a function is from a first set to a second set, it is quite possible that the second set is the same as the first set. In that case the range of the function is contained in the domain. Then the function is said to be from the set to itself: f:U → U. The function then carries objects in the set back into the same set. For example, the function f: N₅ → N₅ defined by

1 →3, 2 → 2, 3 → 5, 4 → 4, 5 →1 carries N₅ to itself. The images f(1), f(2), f(3), f(4), f(5) are objects 3,2,5,4,1 in N₅. But notice that the images f(1) is not 1, f(3) is not 3, and f(5) is not 5. But f(2) = 2 and f(4) = 4. Intuitively speaking, f moves objects 1,3, and 5, but does not move 2 and 4.

[3.4] (Fixed points) A function from a set to itself leaves an object fixed if and only if it carries that object onto itself.
Notation: b is a fixed point of f if and only if f(b) = b.

The identity function leaves every object fixed. The other extreme is also possible; a function may have no fixed points whatsoever. For example, the function g defined by

1 →3, 2 → 3, 3 → 5, 4 →3, 5 →3 has no fixed points. Every object is "moved" to a different object.
Fixed points of functions play important roles in various parts of mathematics. Some lengthy articles are written about them.

-----

For the integers in J, it is possible to combine by multiplication two integers and obtain a single integer which is the product. Under certain conditions it is possible to combine functions, that is, to derive a single function from two given functions. Suppose f: N₅ → N₆    g: N₆ → N₇ where N₅ = {1,2,3,4,5},    N₆ = {1,2,3,4,5,6},    N₇ = {1,2,3,4,5,6,7},    Then, ussing first the "arrow nottion", define f and g by
   f:    1 → 2,    2 → 2,    3 → 6,    4 → 5,    5 → 4
   g: 1 → 4,    2 → 1,    3 → 4,    4 → 6,    5 → 3,    6 → 7
Then form the product fg by combining two arrows for each object in N₅:
   fg:    1 → 2 → 1,    2 → 2 → 1,    3 → 6 → 7,    4 → 5 → 3,    5 → 4 → 6
Taking the first and third of each triple,the result is
   fg:    1 → 1,    2 → 1,    3 → 7,    4 → 3,    5 → 6

Repeat the above using the same functions but with function notation.

f(1) = 2, f(2) = 2, f(3) = 6, f(4) = 4, f(5) = 5 and g(1) = 4, g(2) = 1, g(3) = 4, g(4) = 6, g(5) = 3, g(6) = 7, Then gf can be evaluated as follows: gf(1) = g(2) = 1
gf(2) = g(2) = 1
gf(3) = g(6) = 7
gf(4) = g(4) = 6
gf(5) = g(5) = 3 Then deleting expressions g(2), g(4), g(5). g(6) from the chains of equalities: gf(1) = 1
gf(2) = 1
gf(3) = 7
gf(4) = 6
gf(5) = 3 Therefore, gf is a function from N₅ to N₇: gf: N₅ → N₇.

Intuitively speaking, looking at g and f separately, the function gf carries objects in N₅ onto objects in N₆. Then g carries these objects from N₆ onto objects in N₇. The notation for this interpretation is g(f(x)).
But looking at gf as a single function, it carries objects in N₅ directly onto objects in N₇, ignoring N₆ completely. The notation for this interpretation is (gf)(x). But usually the excess parentheses are omitted, and the notation gf(x) is sufficient. Then either interpretation is allowed. The product gf is written in referse order so that f carries first objects from the first set into the second set. Intuitively speaking, gf is written backward, so that f is the first to carry objects in g(f(x)). Some algebraists prefer to write the function notation (x)f Intuitively speaking, gf is written backward, so that f is the first to carry objects in g(f(x)). Some algebraists prefer to write the function notation (x)f instead of f(x) so that the product fg can be written (x)fg. In these discussions the notation f(x) is used and not (x)f, and hence gf iss the product of f and g. But for clarity, the arrow notation often will be used, where fg is the product of f and g.

[3.5] (Product of functions) Let a first function carry all objects of a first set into a second set, and a second function carry all objects of that second set into a third set. Then the product or composition of a first function and a second function carries all objects of the first set into the third set, where the second function carries the images of the first function into the third set.
Notation: Let f:U → V and g:V → W. Then gf: U → W, and for any x in U, gf(x) = g(f(x)).

Quite often two fuknctions are defined by what they both do to variable x. For example using
verbal notation
Define f and g as follows:
f carries x onto 2x and g carries x onto x + 1.
before attempting to compute theproduct, replace the image 2x by y. At the same time replace all the x's in the definition of g by y'x.
Then f carries x onto y and g( carries y onto y + 1.
Then the product will carry x onto (y and then onto) y + 1.
Replace all y's by 2x to get: the product will carry x onto 2x + 1.

arrow notation:
Define f and g as follows
   f: x → 2x    and    g: x → x + 1
Replace image 2x by y. at the same time replace all the x's in teh definition of g by y's
   f: x → y    and    g:y → y + 1
Then
   x → y → y + 1
replace all y's by 2x to get
   x → 2x → 2x + 1
Therefore
   fg: x → 2x + 1.

function notation
Define f and g as follows
   f(x) = 2x    and    g(x) = x + 1
Replace image 2x by y. at the same time replace all the x's in teh definition of g by y's
   f(x) = y    and    g(y) = y + 1
Then
   gf(x) = g(y) = y + 1
Replace all y's by 2x to get
   gf(x) = g(2x) = 2x + 1
Therefore
   gf(x) = 2x + 1.

Notice that the range of f in [3.5] is contained in the second set V. The domain of g is the entire second set V. Therefore, the range of f is contained in the domain of g. This last statement is the necessary and sufficient condition that gf can be formed (computed). Some people may say that the condition is equivalent to the statement g is conformable to f. The reader can show that the product of g and f is 2(x + 1). this shows that in general, product of functions is not commutative. It willb be assumed here that the product of functions is associative:
the product of f and (the product of g and h) = the product of (the product of f and g) and h.

Section 4: Three Special Functions

[4.1] One of the special functions has already been introduced in the previous section, namely, a function from a first set onto a second set (See [3.2b]).

Intuitively speaking such a function "covers" the second set with a saturation barrage of objects carried from the first set. Every object in the second set is an image of some object in the first set. The range of the function is the entire second set.

Another special function is the following:

[4.2a] (One-to-one functions) A function from a first set to a second set is one-to-one if and only if it carries distinct objects from the first set onto distinct objects in the second set.
Notation1: if x₁ is not equal to x₂ then f(x₁) is not equal to f(x₂). Notation2: 1-1 means "one-to-one".

Example [4.2i] The function in Fig IV above is not one-to-one because it carries distinct objects 1 and 2 onto a single object 2.

Example [4.2ii] Tie the boats to poles differently:

1 → 2, 2 → 3, 3 → 4, 4 → 5, 5 → 6 Then different boats are tied to different poles. This function is 1-1.

Definition [4.2a] is useful if the first set (domain) is very small. Suppose there are 1000 boats and 2000 poles. The boats are tied up systematicly to the poles according to the rule:

x → 2x A partial check shows that 1 → 2, 2 →4, 3 → 6, .., 1000 → 2000 is a one-to-one function for 1,2,3,1000. A better method is to modify definition [4.2a] and obtain an equivalent definition [4.2b]:

[4.2b] (One-to-one functions) A function from a first set to a second set is one-to-one if and only if the only way that two (or more) objects in the first set can be carried by the function onto the same object in the second set is that those objects in the first set be equal.
Notation: If f(x₁) = f(x₂) then x₁ = x₂.

The equality f(x₁) = f(x₂) says that f carries objects x₁ and x₂ onto the same object in the second set. Then the implication

(*) if f(x₁) = f(x₂) then x₁ = x₂ requires that the objects x₁ and x₂ be the same.
The implication in the notation for [4.2a] is the contrapositive of implication (*). Therefore, the implications are equivalent and so the other parts of [4.2b] and [4.2a] are equivalent. In most discussions implication (*) is more eqsily applied than the implication given in [4.2a].

Example [4.2iii] Let f:N → N be the doubling function f(x) = 2x. To show that f is 1-1 start with the implication

f(x₁) = f(x₂) ==> 2x₁ = 2x₂ Then produce a chain of implications: f(x₁) = f(x₂) ==> 2x₁ = 2x₂ ==> x₁ = x₂ [after dividing by 2]
Often the implication (*) is proven by a chain of implications connecting the hypotheses and the conclusion, especially if the function is given by a formula. Here it was f(x) = 2x.
In some proofs [4.2a] is used.

An important function is both one-to-one and "onto":

[4.3] (One-to-one correspondences) A one-to-one correspondence between a first set and a second set is a one-to-one function from the first set onto the second set.
Notation: f:U → V carries distinct objects in U onto distinct objects in V, and every object in V is an image of some object in U.

There are to parts to proving that a function is a one to one correspondence:
the function is one-to-one;
the function is onto (the second set).

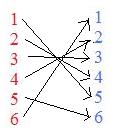
Example [4.3a] Let N₆ and N₆ both be the set of the first six natural numbers. Define f by
1 → 5, 2 → 4, 3 → 3, 4 → 2, 5 → 6, 6 → 1
The adjacent figure is a vertical representation of this function..
Clearly f does not carry anything in N₆ onto two different things in N₆. Therefore, f is 1-1.
Also every thing in N₆ is an image (has an arrow pointing to it). Therefore, the function is "onto", and it qualifies as a one-to-one correspondence.

Example [4.3c] The identity function on any non-empty set is a one-to-one correspondence.

Example [4.3d] Let g: J → J be a function on the set of all integers, defined by

g(x) = x + 1 Therefore, g carries each integer onto the next one that is larger.
g is 1-1 because g(x₁) = g(x₂) ==> x₁ + 1 = x₂ + 1 ==> x₁ = x₂.
g is "onto" because for any x in J, g carries x-1 onto x. So each x is an image.
Therefore, g is a 1-1 correspondence on J.

In Example [4.3a] the function there is a one-to-one correspondence between N₆ and N₆. Both sets have the same number of objects. This idea may be extended to all kinds of sets.

[4.4] (Having the same number of objects) A pair of sets have the same number of objects if and only if there is a one-to-one correspondence between them.

This definition is the basis for counting. There are 100 balls in a bag if and only if there is a one-to-one correspondence between the set N₁₀₀ and the set of all those balls. But [4.4] also applies to infinite sets. As an example, there are the same number of negative integers as positive integers. the correspondence -n ↔ n is one-to-one and onto.
Click here for further discussion of infinite sets.

-----

An important question is: if two functions have a common property does their product have that property? The following answers this question affirmatively for the three special functions.

[4.5] (Preservation of special functions through products) Let f be a function from a first set to a second set, and g be a function from the second set to a third set. [If arrow nottion is used beetween objects, then replace gf by fg.]Then the product gf is a function from the first set to the third set.
  (a) if f and g are "onto", then gf is "onto".
  (b) if f and g are one-to-one, then gf is one-to-one.
  (c) if f and g are one-to-one correspondences then gf is a one-to-one correspondence.

Part (a)
To prove gf is "onto." Let z be any object in the third set. Since g is "onto" then there is an object y in the second set such that z = g(y). But since f is "onto" there is an object x in the first set such that y = f(x). Then z = g(y) = g(f(x)) = gf(x). Therefore, gf is "onto", because z is any object in the third set, and x is an object in the first set, so z is an image of x.

Part (b)
To prove gf is one-to-one. Let x₁ and x₂ be distinct objects in the first set. Since f is one-to-one, then f(x₁) and f(x₂) are distinct objects in the second set. But g carries distinct objects from the second set into the thrid set. So g(f(x₁)) and g(f(x₂)) are distinct objects in the thrid set. Therefore,
x₁ and x₂ are distinct objects in the first set ==> gf(x₁) and gf(x₂) are distinct objects in the third set set
This proves that gf is one-to-one.

Proof of part (c) follows immediately from part (a) and part (b). According to [4.5], the properties "onto", one-to-one and one-to-one correspondence are preserved through product of functions.

-----

Let f and g be functions from N₅ to N₅ defined by
   f:      1 → 5,   2 → 2,   3 → 4,   4 → 1,   5 → 3
   g:     1 → 3,   2 → 4,   3 → 4,   4 → 5,   5 → 3
The reverses of f and g are:
   reverse f:      1 → 4,   2 → 2,   3 → 5,   4 → 1,   5 → 3
   reverse g:      3 ~ 1,   3 ~ 5,   4 ~ 2,   4 ~ 3,   5 ~ 4
Then reverse f is a function from N₅ to N₅. But reverse g is only a relation between N₅ and N₅. These two functions f and g show that the reverse of a function may or may not be a function. Intuitively speaking, there is something "defective" with singular functions like g.
A function is singular if its reverse is not a function (but only a relation).
On the other hand non-singular functions like f are not "defective".
The reverse of a non-singular function is called the inverse of the function.
Notation: f^-1 = inverse of a non-singular function f. A singular function like g has no inverse. Therefore, g^-1 has no meaning, and cannot be used.

What determines whether a function is singular or non-singular? A close inspection of the blue numbers in the definition of f shows that every number in N₅ appears. Therefore f is a function onto N₅. All red numbers appear once and only once. This makes f one-to-one. This discussion indicates that only for one-to-one correspondences is the reverse relation a function.

[4.6] (Non-singular functions) A function is non-singular if and only if the function is a one-to-one correspondence.

Click here to see a discussion supporting [4.6].

Let f be a function from a first set to a second set. In summary the following are equivalent terms:
f is non-singular, the inverse f^-1 exists and is a function, f is a one-to-one correspondence
f is singular, the reverse of f is only a relation, not a function f is not a one-to-one correspondence.
A singular function fails to be "onto" the second set, to be one-to-one or fails to be both "onto" and one-to-one.

[4.7] (Product of a function and its inverse) Given a function, which is a one-to-one correspondence, from a first set to a second set. Then its inverse (reverse) is a function from the second set back to the first set and is itself a one-to-one correspondence..
  (a)The product of the given function and its inverse is the identity function on the first set.
  (b) The product of the reverse function and the given function is the identity function on the second set.
Notation: (a) f^-1f = I_{first set}.      (b) ff^-1 = I_{second set}.

If f carries object x in the first set onto object y in the second set, then as a reverse function, f^-1 carries y back onto x. Therefore, for any object x in the first set, f^-1(f(x)) = f^-1(y) = x = I(x). Then f^-1f(x) = I(x) for every x in the first set. By equality of functions [3.3], f^-1f = I.

For a proof that the inverse of a one-to-one correspondence is itself a one-to-one correspondence click here.

Often [4.7] is used as a definition of inverse of a function if the inverse exists. The term "reverse" is not used in other works.

Section 5: Permutations

Consider any finite collection of distinguishable objects. Establish a relation between all of the objects so that the relation is actually a one-to-one correspondence.

[5.1a] (Permutations) A one-to-one correspondence between a finite collection of distinguishable objects and the same collection is called a permutation on the collection.

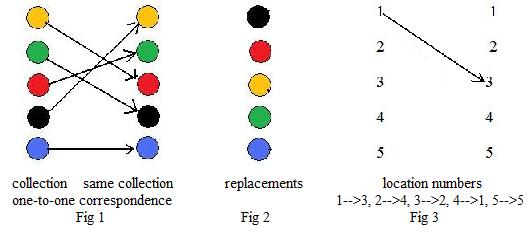This is the standard definition of a permutation. Fig 1 shows two copies of a collection of five colored balls and a one-to-one correspondence from one copy to the other, so it is a one-to-one correspondence of the collection with itself. Fig 1 is a pictorial example of a permutation as defined in [5.1a].

Fig 2 is the result of replacing balls in the right column of Fig 1 by balls in the left column. The ball at the tail of the long arrow replaces the ball at the head of the arrow. For example, the yellow ball in the left column replaces the red ball in the right column. Therefore, the column on the right of Fig 1 has a change of apparance from the replacements as shown in Fig 2.

In Fig 3 all balls in Fig 1 are replaced by location numbers from N₅. Long arrows in Fig 1 are replaced by short arrows between location numbers. For example, in Fig 1, a long arrow links the orange ball in the left column with the red ball in the right column. These balls have location numbers 1 and 3. Therefore, 1 → 3 expresses what the long arrow does. The other long arrows in Fig 1 are replaced by short arrows between numbers in N₅. The collection of all short arrows 1 → 3, 2 → 4, 3 → 2, 4 → 1, 5 → 5
shows actually a function from N₅ onto N₅, in fact a one-to-one correspondence. In this section the following form of [5.1a] will be used:

[5.1b] (Permutation of location numbers) A permutation of n objects is a one to one correspondence between N_n and itself, where N_n supplies the unique location numbers of the objects.

A graphical representation of locations and their numbers will often be the following:
The locations of n objects will be conveniently represented by a horizontal row of n blanks. Sometimes the objects themselves will occupy the blanks. Unter the blanks are the numbers from N_n in increasing order. In discussions of permutations, another collection of blanks and numbers may be included.

		_  _  _  _  .... _  _		_  _  _  _  .... _  _
		1  2  3  4           n 		1  2  3  4           n

[5.2] (Arrangements) A collection of n objects is in the form of an arrangement if and only if each object is in a place that has a unique location number taken from 1,2,...,n . The complete assignment is called a sequential ordering of the n objects.

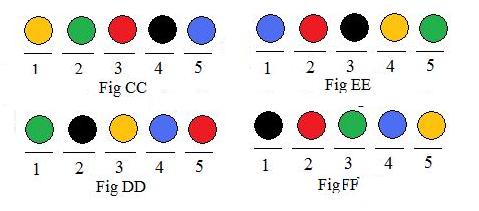In the figures to the right, the same five balls are involved in all four figures. Fig CC, Fig DD, Fig EE and Fig FF show different arrangements. (There are actually 120 different arrangements of of the same five distinct objects.)

When a new arrangement is made from an existing arrangement, the same locations are used, but each object has a specific destination whch may have a different location number. For example, in moving the balls around to go from Fig CC to Fig EE, the following "plan" tells how to do it:
1 → 4, 2 → 5, 3 → 2, 4 → 3, 5 → 1
where each arrow involves a ball of a different color. Similarly, for balls re-arranged from Fig EE to Fig FF,
1 → 4, 2 → 2, 3 → 1, 4 → 5, 5 → 3
These are arrow notations for two functions, in fact one-to-one correspondences between N₅ and itself. According to [5.1b] they are also permutations of the location numbers.

The identity function I which leaves all the location numbers fixed (and hence moves nothing to get a different arrangement) is considered a trivial permutation.

-----

What is the simplest non-trivial permutation of location numbers? It is any permutation that moves exactly two objects. Examples are:
   1 → 4, 2 → 2, 3 → 3, 4 → 1, 5 → 5                                                      1 ↔ 4
   1 → 1, 2 → 2, 3 → 5, 4 → 4, 5 → 3                                                      3 ↔ 5
   1 → 1, 2 → 3, 3 → 2, 4 → 4, 5 → 5                                                      2 ↔ 3
An elementary permutation leaves all numbers in N_n fixed except for two numbers. It interchanges the objects in these two locations. The two-headed arrow

i ↔ j is suggestive of interchange of two natural numbers i and j. A notation (cyclic) later will represent an elementary permutation of location numbers as (i j).
-----

Sometimes it is useful to know how many arrangements can be placed on n blanks.

[5.3] (Number of arrangements) From a source of n objects there are exactly n! arrangements to fill n locations, where n is any natural number.
Notation: n! = 1x2x...xn = product of all natural numbers from 1 up to and including n. (read n! as n factorial)

On N₃ ={1,2,3} there are 3! = 6 permutations. On N₄ = {1,2,3,4} there are 4! = 1x2x3x4 = 24 permutations.
Table:
1!=1, 2!=2, 3!=6, 4!=24, 5!=120, 6!=720, 7!=5040, 8!=40320, 9!=362880, 10!=3628800, 11!=39916800, 12!=479001600, 13!=6227020800. It will be convenient to define 0! = 1.
Click here to see a discussion supporting [5.3a].

Although definition [5.3a] is more frequently used in these discussions, there is a more general and more common definition. Definition [5.3a] relates objects in the first arrangement indirectly with objects in the second arrangement by their location numbers. This relation is actually a one-to-one correspondence between objects in the source and objects in that same source.

-----

The arrow notation is one way to display a function. The notation b → c is read "b is carried onto c". It may haappen that somewhere there is another arrow c → d where the head of the first arrow (c) is the same as the tail of the second arrow (c). Here "c in turn is carried onto d". Two things may be done with such arrows:

b → c → d and b → d In the situation on the left, the arrows have been attached to each other at the common element c. "b is carried onto c which is carried onto d." In the situation on the right the common element c is omitted and a single arrow attaches the first and third numbers. "b is carried directly onto d". This last situation leads to the following:

[5.4] (Products) The product of permutations is a permutation.

The statement follows immediately from the fact that the product of one-to-one correspondences is a one-to-one correspondence.

Example:
Let 4,3,5,1,2 and 5,2,4,1,3 be two arrangements of the numbers in N₅. To find their product. First, convert them to functions:

1 → 4, 2 → 3, 3 → 5, 4 → 1, 5 → 2; 1 → 5, 2 → 2, 3 → 4, 4 → 1, 5 → 3 The following is the computation for getting the product: 1 → 4 → 1, 2 → 3 → 4, 3 → 5 → 3, 4 → 1 → 5, 5 → 2 → 2 The actual product is 1 → 1, 2 → 4, 3 → 3, 4 → 5, 5 → 2

[5.5] (Inverses) The inverse of a permutation is a permutation.
Notation: if f is a permutation on some finite set, then f^-1 is also a permutation on that set.

The statement follows immediately from the fact that the inverse of a one-to-one correspondence is a one-to-one correspondence ([4.5]).

Example:
The arrangement 5,2,4,1,3 represents a permutation. Find its inverse.
Convert this arrangement into arrow notation (replacing the numbers of the normal arrangement with this arrangement):

1 → 5, 2 → 2, 3 → 4, 4 → 1, 5 → 3 Reverse arrows and sort: 1 → 4, 2 → 2, 3 → 5, 4 → 3, 5 → 1 Therefore, the arrangement 4,2,5,3,1 is the inverse of the arrangement 5,2,4,1,3.

As a check, form the product of the original function and its inverse:

1 → 5 → 1, 2 → 2 → 2, 3 → 4 → 3, 4 → 1 → 4, 5 → 3 → 5 The fact that the first and third numbers in each chain of two arrows are the same, means the inverse was correctly computed.

-----

The following permutation on N₅ in function notation (*) 1 → 5, 2 → 4, 3 → 1, 4 → 3, 5 →2 repeats each number twice, once before the arrow and once after the arrow.

In the following chain of arrows 1 → 5 → 2 → 4 → 3 → 1 except for 1, each number appears once and only once. This exception can be removed by bending the arrows and making a circle, as shown in the adjacent figure Fig CN.
The figure and function notation (*) both say what numbers are carried onto what numbers: 1 is carried onto 5, 2 is carried onto 4, 3 is carried onto 1, 4 is carried onto 3, and 5 is carried onto 2 Therefore, the the figure and (*) determine the same permutation.
The figure can be represented by the notation (**) (1 5 2 4 3) so that each number appears once and only once. The horizontal notation (**) and figure represent what is called a cycle
Notice:
Spaces, not commas, separate numbers inside the notation for a cycle.
No duplicates appear in a cycle.
The next number after the end of a cycle is the number at the beginning.
Usually the beginning of a cycle has the smallest number in the cycle.

[5.6] (Cycle) A cycle (a₁ a₂ ... a_k ) of numbers taken from a source N_n where n is not less than k, denotes the carrying of numbers

a₁ → a₂, a₂ → a₃, ... a_k-1 → a_k, a_k → a₁. with the following conventions and conditions:
  (a) Spaces, not commas, separate numbers inside the notation for a cycle.
  (b) No duplicates appear in a cycle.
  (c) The next number after the end of a cycle is the number at the beginning of the cycle.
  (d) Usually the beginning of a cycle has the smallest number in the cycle.

A cycle may or may not involve all numbers of the source. For example (2 5 3) does not involve all numbers in source N₅. until what happens to the missing numbers is known, this cycle alone might not represent the desired permutation on the source. Since a permutation must involve all numbers in the source, involvement of numbers 1 and 4 are needed. Let (1 4) be the cycle involving them. The permutation can be defined by (a product of) two (disjoint) cycles

(1 4) (2 5 3) In chains of arrows notation: 1 → 4 → 1, and 2 → 5 → 3 → 2.
In arrow notation: 1 → 4, 2 → 5, 3 → 2, 4 → 1 5 → 3.

Consider now the cycle (1 4 2 5) with numbers taken from source N₅. In chains of arrows, this cycle represents

1 → 4, 2 →5, , 4 → 2, 5 → 1 The only way to complete this notation for a permutation is 3 → 3. Notice this means that 3 is a fixed point. Also the needed cycle is (3): (1 4 2 5)(3) involves all numbers in the source and is a permutation on the source.

[5.7] (Trivial cycle) A cycle is trivial (has only one number in it) if and only if that number is a fixed point in the arrow notation.

The permutation on N₇ defined by

(1)(2 5 7)(3)(4 6) has fixed points 1 and 3.
Often the trivial cycles are not written: (2 5 7)(4 6) Then the source must always be known in case the largest number in the source makes a trivial cycle that is omitted.
With the convention of not writing trivial cycles, any cycle alone represents a permutation.

[5.8] (Equality of cycles) Two cycles are equal if and only if the arrow notations of them are the same.

For example, Let the source be N₅. Each of the cycles

(1 5 2 4 3), (5 2 4 3 1), (5 2 4 3 1), (2 4 3 1 5), (4 3 1 5 2) represent the same function 1 → 5, 2 -- > 4, 3 →1, 4 → 3, 5 → 2. The five cycles are equal. Each of them can be represented by the same circular figure for (1 5 2 4 3). See Fig CN above.
In these discussions the first number in a cycle, written horizontally, is the smallest number in the cycle. So (1 5 2 4 3) would be the standard form for this cycle.

=======

Cycles without a common object in them are called disjoint. The cycles

(1 3 5 7) and (2 4 6 8) are disjoint.

It is possible that not all the objects in the source are involved in cycles. If N₈ is the source then the cycle

(5 7 2 6 8 4) does not involve 1 or 3. Constructing the arrow notation from the given cycle: 2 → 6, 4 → 5, 5 → 7, 6 → 8, 7 → 2, 8 → 4 As expected, 1 → _ and 3 → _ are not completed. So that every object in the source appears only once, only 1 and 3 can fill in the blanks. Two possibilities are: 1 → 1 and 3 → 3 or 1 → 3 and 3 → 1 The latter is not possible since an additional cycle (1 3) would have to follow the given cycle: (5 7 2 6 8 4)(1 3) But (1 3) was not included in what was given. So 1 → 1 3 → 3 must satisfy the stiuation. Their cyclic notations are (1) and (3). A cycle containing just one object is called trivial. In arrow nottion it is always a fixed point. Often trivial cycles are not included in a complete cyclic representation of a permutation. This convention means that objects in a source but not appearing in any of the cycles (in cyclic notation) of a permutation are considered fixed points.
The final arrow notation is: 1 → 1, 2 → 6, 3 → 3, 4 → 5, 5 → 7, 6 → 8, 7 → 2, 8 → 4 The following cyclic notation involves all objects in the source and also shows the trivial cycles: (2 6 8 4 5 7)(1)(3) which is equivalent to (2 6 8 4 5 7) The inclusion of trivial cycles (fixed points) in cyclic notation is not necessary except in one situation - when the identity permutation is written: I = (1) where every object in the source is a fixed point. Of course, the largest location number must be known in every situation, in case that number is a fixed point and not written in cyclic notation.

[5.9] Two permutations in the form of disjoint cycles are equal if and only their functions in arrow notation are equal.

It is possible that two or more cycles are not disjoint. Then they are considered as products of permutations. Each can be coverted to arrow notations and then the product can be computed. Then that result can be converted back to cyclic notation.

-----

Every cycle has a smallest natural number in it. A cycle is in standard form if its left most number in the smallest in the cycle. For example,

(3 6 10 21), (6 7 9 8 10), (1 3 7 6 4) are in standard form. But (7 9 8 4 10 12) is not in standard form because the smallest number 4 is not written first. The equivalent cycle (4 10 12 7 9 8) is in standard form.
Cycles have a size. The length of a cycle is the number of natural numbers in it.

[5.10] (Parity of a cycle) A cycle is even if its length + 1 is even, and odd if length + 1 is odd.

The above cycles

(3 6 10 21), (6 7 9 8 10), (1 3 7 6 4), (7 9 8 4 10 12) are (4+1)odd, (5+1)even, (5+1)even, (6+1)odd permutations respectively.