[4.11] A permutation is a non-singular transformation on a finite set.

In [4.2] I,F,T are permutations on the set because the set is finite (has 4 elements) and those transformations are non-singular.

In [4.11] a more technical definition of a permutation was given. The following is a more familiar description:

[4.12] A physical permutation is a rearrangement of objects in a row. Intuitively speaking, the objects are picked up and put back into places in the same row (usually in a different order). No objects are lost, no new objects are added, so that the row is filled again with the same objects.

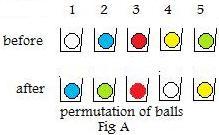Suppose five balls of different colors are placed in containers in a row as shown in the top row of Fig A. Exactly one ball is in each of the containers. A physical permutation takes place by picking up the balls and putting them back into the containers. The results of this action are shown in the bottom row of Fig A. Again, exactly one ball is in each of the containers. The action has caused a rearrangement of the balls.

Since the containers are in a row, there is a first container, then a second container,... etc. To describe the action more exactly, attach permanently the positive integers in P₅ = {1,2,3,4,5} to the containers. Now trace the movements of the individual balls; The physical permutation carries the white ball from container 1 to container 4, the blue ball from 2 to 1, etc. The entire action, call it T, can be completely described by the following function notation:
[*]

T
1 --> 4
2 --> 1
3 --> 3
4 --> 5
5 --> 2 Obviously T is a transformation on P₅. It is one-to-one because no container in the bottom row of Fig A has more than one ball in it. It is "onto" because all the containers in the bottom row has a balls. Therefore, the transformation T is a one-to-one correspondence and is non-singular.

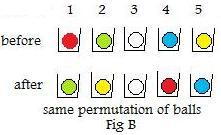The reader can now verify that the permutation in Fig B is the same as the permutation in Fig A. The permutation used in the rearrangement of balls in Fig A is the same used in the rearrangement of balls in Fig B. The same permutation could be used to reassign five people already in a five room motel to other rooms.

The rearrangement can be "undone" and objects put back to where they were originally. If the arrows in [*] are reversed then

4 --> 1, 5 --> 4, 3 --> 3, 1 --> 2, 2 --> 5 and sorted: T^-1
1 --> 2
2 --> 5
3 --> 3
4 -- > 1
5 --> 4 the inverse permutation T^-1 is obtained. The reader can check that the products TT^-1 = I and T^-1T = I. All these remarks motivate the following definition:

Another notation for the permutation is the "two row" notation: