Return to main page
Additional Material for Chapter 2
Measuring Angles
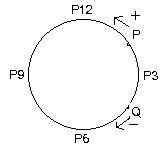 Let P3,P6,P9,P12 be points on the rim of a circular clock. They correspond to the numbers of the hours. (See the adjacent figure.) To go from P3 to P9 the tip of the large hand must pass over P6. Motion along the arc P3,P6,P9 said to be clockwise for the obvious reason. Motion along the arc P3,P12,P9 is counter-clockwise.
Let P3,P6,P9,P12 be points on the rim of a circular clock. They correspond to the numbers of the hours. (See the adjacent figure.) To go from P3 to P9 the tip of the large hand must pass over P6. Motion along the arc P3,P6,P9 said to be clockwise for the obvious reason. Motion along the arc P3,P12,P9 is counter-clockwise.
It is easy to apply this idea to any circle by looking down upon the circle and comparing it to the face of a clock. The figure also shows a point P moving along a circle with a counter-clockwise motion. The point Q is moving with a clockwise motion. It is customary to call counter-clockwise motion positive(+), and clockwise motion negative(-). If P is a car on a circular race track, then the center of the circle is to the left side of car. For car Q the center is nearer to the right side of the car.
If a point moves with a counter-clockwise motion along an arc then the arc becomes a positive path. Clockwise motion goes along a negative path. P3,P6,P9 is a negative arc, but P3,P12,P9 is a positive arc. There are two arcs joining two points on a circle, a positive arc and a negative arc.
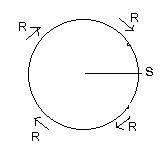 If R is a racecar a circular racetrack, it must have a fixed starting point S somewhere on the track. In a drawing it is customary to choose the location of S as the intersection of a horizontal half-line to the right and the circle. (In our clock notation it would be point P3 which correcsponds to the 3rd hour mark.) The racecar R makes one (complete) revolution around the track when it passes through S for the first time. In the adjacent figure the car makes -1 revolution. Continuing the motion R makes n revolutions when it passes through the starting point S for the n-th time. The number n is positive or negative according to whether the motion is counter-clockwise or clockwise around the circle. For example, -4 revolutions means R is passing through S for the fourth time and going around the circle in a clockwise motion. 5 revolutions means 5 times around the circle in a counter-clockwise direction and passing through S. Using the notation n rev to mean n revolutions, the meanings of 2 rev, 403 rev, -8 rev, -95 rev are obvious.
If R is a racecar a circular racetrack, it must have a fixed starting point S somewhere on the track. In a drawing it is customary to choose the location of S as the intersection of a horizontal half-line to the right and the circle. (In our clock notation it would be point P3 which correcsponds to the 3rd hour mark.) The racecar R makes one (complete) revolution around the track when it passes through S for the first time. In the adjacent figure the car makes -1 revolution. Continuing the motion R makes n revolutions when it passes through the starting point S for the n-th time. The number n is positive or negative according to whether the motion is counter-clockwise or clockwise around the circle. For example, -4 revolutions means R is passing through S for the fourth time and going around the circle in a clockwise motion. 5 revolutions means 5 times around the circle in a counter-clockwise direction and passing through S. Using the notation n rev to mean n revolutions, the meanings of 2 rev, 403 rev, -8 rev, -95 rev are obvious.
Visually P9 is half-way around the circle from S=P3. Therefore P9 is 1/2 a revolution around the circle from S. P12 is 1/4 revolution from S. Notice also that P12 is -3/4 revolution from S, going in the clockwise direction. Using a starting point and revolutions and fractions thereof, every point on the circle can be located. Although this method of measuring relative arc-distance along a circle of any radius, the unit circle will be the focus of this discussion. For that circle the revolutions and fractional parts can be equated to actual distances, which are lengths of arcs.
The unit circle has a circumference of 2π. Therefore, as measure along the circle, 1 rev = 2π, 1/2 rev = π, 1/4 rev = π/2. Also -1/2 rev = -3/4π = -3/4 rev. Measure of arc-length of the unit circle is given in radians. So π radians is the measure of half of the unit circle, the semi-circle. (Radian measure is never given in feet, yards, meters, or other units of distance..... It is said to be dimensionless because the actual lengths of the unit radius and therefore the circumference of the unit circle are not given in feet, yards, meters,....)
For any point P that is on a circle there is a segment OP joining it and the center O. Extend the segment past the point P to form a ray. Ray OP does not pass through the center O to the other side. For this reason a ray is also called a half-line.
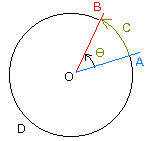 For two points A and B there are two half-lines through them and the origin. These half-lines intersect at the origin O and form an angle θ there. Since the vertex is at the center O of the circle the angle is called a central angle. In the figure arc ACB is positive so central angle θ is positive. There is another central angle without a name, but its arc is ADB which is negative. So that angle is negative. The half-line OA is called the initial side of the angle, and the half-line OB is the terminal side. The arc also gives its directed length to the measure to the angle. In the figure, approximately θ = 1/8 rev = π/4 radians because the arc ACB is positive and has length approximately equal to 1/8 of the circumference.
For two points A and B there are two half-lines through them and the origin. These half-lines intersect at the origin O and form an angle θ there. Since the vertex is at the center O of the circle the angle is called a central angle. In the figure arc ACB is positive so central angle θ is positive. There is another central angle without a name, but its arc is ADB which is negative. So that angle is negative. The half-line OA is called the initial side of the angle, and the half-line OB is the terminal side. The arc also gives its directed length to the measure to the angle. In the figure, approximately θ = 1/8 rev = π/4 radians because the arc ACB is positive and has length approximately equal to 1/8 of the circumference.
Although revolutions and radians give measurement to central angles, there is a third measurement, called degree. By definition there are 360 degrees (written 360°) in 1 revolution. (This seemingly arbitrary figure may be related to the number 365, equal to the number of days in a year.) A motion of 1° travels a very small distance on the unit circle. The distance is equal to 1/360 of the circumference. Very common in elementary plane geometry are angles 30°, 60°, 90°, 180°.
Using the various measures,
the size of a right angle = 1/4 rev = π/2 radians = 90°
.
the size of a straight angle = 1/2 rev = π radians = 180°.
the size of a complete revolution = 1 rev = 2π radians = 360°.
As indicated before, the term "radians" is not needed.
For exercises on conversions of angle meassurements click here
Consider the angle whose measure is 390°. It seems larger than 1 rev = 360°. If the racecar R went 390° around the circular track and then stopped, he would be 30° beyond the starting point, because 390 = 1(360) + 30 = 1 rev + 30. Similarly, 10000° = 27 rev + 280°.
A geometrical figure cannot show the number of revolutions for a large number of degrees. It can show in degrees how far beyond the starting point the race car stops. In general, given a large number of degrees, divide it by 360. The quotient = number of revolutions, and the remainder (the excess) in degrees locates the stopping point beyond the starting point.
The measurement of two angles are said to be equivalent if their difference is an integral number of rotations. θ and φ are equivalent if θ - φ = n rev where n is a whole integer. (do not confuse equivalence with equality.)
Examples: 370° and 10° are equivalent because 370 - 10 = 360 (1 rev). 10000° and 280° are equivalent because their difference is equal to 27 revolutions. To prooduce the numbers, divide 280 into 10000 to get a quotient 27 and a remainder of 280: 10000 = (27)(360) + 280. 7π and 3π radians are equivalent radian measurements because their difference is equal to 4π which is 2 revolutions. (2π = 1 rev) Note: equivalence is an important concept in modern algebra.
Now suppose the initial side of central angle is fixed and coincide with the positive real axis, which contains the unit vector1. Algebraicly, 30°, 390°, 750°, -330°, -690° ... are equivalent measurements. (But they are not equal numbers!) Geometrically, the terminal sides of all these equivalent angles coincide with the terminal side of 30°.
Using the cis notation, cis(30°) = cis(390°) = cis( 750°) = cis(-330°) = cis( -690°).
In general, cis (θ + n rev) = cis θ where n is any integer, positive or negative
Another geomitric interpretation: two central angles (with initial sides coinciding with the positive real axis) are equivalent if their terminal sides intersect with the unit circle at the same unit complex number (point). θ and φ are equivalent if and only if cis θ = cis φ (unit complex numbers on the unit circle).
Notice that geometrically cis θ locates the position of the terminal side of central angle θ if the initial side is drawn. More exactly, cis θ locates the point B if point A is known, where both points are on the unit circle, and θ is the central angle AOB.
A natural way to relate central angle to a unit complex number
The real number e = 2.71828..... is useful in the study of calculus. Integer exponents apply with the usual meanings: e² = (e)(e) = 7.3890......., e³ = (e)(e)(e) = 20.0854... . It is possible to use complex numbers as exponents: ez.
If θ is any real number (or in radians) it can be shown that eiθ is a unit complex number. Moreover, that unit complex number is the same as cis θ:
eiθ = cis θ.
Let θ = π radians. then the expression becomes:
(*) eiπ = -1
because cis π = -1. The contents of expression (*) involves some interesting numbers. e is a constant useful in calculus, i is the imaginary unit, π = 3.14159... is another constant used in geometry to compare the circumference and diameter of circles, and -1 is the first negative integer.
A geometric proof of the DeMoivre theorem: cis(θ + φ) = (cis θ)(cis φ)
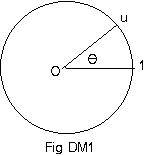
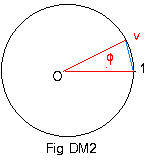
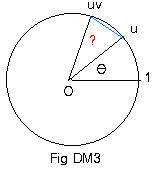
Let u and v be unit complex numbers with central angles θ and φ. (See Fig DM1 and Fig DM2.). Their product uv is also a unit complex number, and is somewhere on the unit circle. (See Fig DM3.)
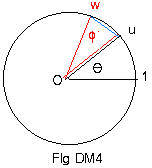
Now locate a unit complex number w that has central angle θ + φ: w = cis(θ + φ).
The plan here is to show that points uv and w coincide. (Fig DM3 and Fig DM4.)
Length of chord u,uv = |uv - u| = |u(v - 1)| = |u||v - 1| = 1|v - 1| = |v - 1| = length of chord 1,v (Fig DM2) = chord u,w (Fig DM4). This means that arc u,w in Fig DM4 is congruent to arc u,uv in Fig DM3. Therefore the central angle ? in Fig DM3 must equal the central angle φ in Fig DM4.
Therefore, cis (θ + φ) = w = uv = (cis θ)(cis φ).
 If R is a racecar a circular racetrack, it must have a fixed starting point S somewhere on the track. In a drawing it is customary to choose the location of S as the intersection of a horizontal half-line to the right and the circle. (In our clock notation it would be point P3 which correcsponds to the 3rd hour mark.) The racecar R makes one (complete) revolution around the track when it passes through S for the first time. In the adjacent figure the car makes -1 revolution. Continuing the motion R makes n revolutions when it passes through the starting point S for the n-th time. The number n is positive or negative according to whether the motion is counter-clockwise or clockwise around the circle. For example, -4 revolutions means R is passing through S for the fourth time and going around the circle in a clockwise motion. 5 revolutions means 5 times around the circle in a counter-clockwise direction and passing through S. Using the notation n rev to mean n revolutions, the meanings of 2 rev, 403 rev, -8 rev, -95 rev are obvious.
If R is a racecar a circular racetrack, it must have a fixed starting point S somewhere on the track. In a drawing it is customary to choose the location of S as the intersection of a horizontal half-line to the right and the circle. (In our clock notation it would be point P3 which correcsponds to the 3rd hour mark.) The racecar R makes one (complete) revolution around the track when it passes through S for the first time. In the adjacent figure the car makes -1 revolution. Continuing the motion R makes n revolutions when it passes through the starting point S for the n-th time. The number n is positive or negative according to whether the motion is counter-clockwise or clockwise around the circle. For example, -4 revolutions means R is passing through S for the fourth time and going around the circle in a clockwise motion. 5 revolutions means 5 times around the circle in a counter-clockwise direction and passing through S. Using the notation n rev to mean n revolutions, the meanings of 2 rev, 403 rev, -8 rev, -95 rev are obvious.
 Let P3,P6,P9,P12 be points on the rim of a circular clock. They correspond to the numbers of the hours. (See the adjacent figure.) To go from P3 to P9 the tip of the large hand must pass over P6. Motion along the arc P3,P6,P9 said to be clockwise for the obvious reason. Motion along the arc P3,P12,P9 is counter-clockwise.
Let P3,P6,P9,P12 be points on the rim of a circular clock. They correspond to the numbers of the hours. (See the adjacent figure.) To go from P3 to P9 the tip of the large hand must pass over P6. Motion along the arc P3,P6,P9 said to be clockwise for the obvious reason. Motion along the arc P3,P12,P9 is counter-clockwise.
 For two points A and B there are two half-lines through them and the origin. These half-lines intersect at the origin O and form an angle θ there. Since the vertex is at the center O of the circle the angle is called a central angle. In the figure arc ACB is positive so central angle θ is positive. There is another central angle without a name, but its arc is ADB which is negative. So that angle is negative. The half-line OA is called the initial side of the angle, and the half-line OB is the terminal side. The arc also gives its directed length to the measure to the angle. In the figure, approximately θ = 1/8 rev = π/4 radians because the arc ACB is positive and has length approximately equal to 1/8 of the circumference.
For two points A and B there are two half-lines through them and the origin. These half-lines intersect at the origin O and form an angle θ there. Since the vertex is at the center O of the circle the angle is called a central angle. In the figure arc ACB is positive so central angle θ is positive. There is another central angle without a name, but its arc is ADB which is negative. So that angle is negative. The half-line OA is called the initial side of the angle, and the half-line OB is the terminal side. The arc also gives its directed length to the measure to the angle. In the figure, approximately θ = 1/8 rev = π/4 radians because the arc ACB is positive and has length approximately equal to 1/8 of the circumference.



