In this section natural numbers will be used most of the time, but a limited use of zero will be allowed. Geometrically, only the part of the number line (including zero) will be considered. That part will be called the non-negative half-line or simply half-line. It contains all of the equally spaced non-negative integers. All the natural numbers locate points on this half-line. Zero locates the only end-point. There is no end-point to the right. The following will be needed:
m/n = q + r/n where q ad r are non-negative integers, 0<r
14/5 = 2 + 4/5, so 14/5 lies between 2 and 3.
93/7 = 13 + 2/7, so 93/7 lies between 13 and 14.
5/8 = 0 + 5/8, so 5/8 lies beetween 0 and 1.
The plus sign is important. If it is omitted then, according to algebraic notation, the numbers are multiplied.
9/4 is NOT equal to 2 times 1/4 but 9/4 = 2 + 1/4. 5/8 is not equal to 0 times 5/8 but 5/8 = 0 + 5/8. The custom of omitting the plus sign gives an incorrect number.
It is easy to modify the construction to show that the point m/n is just one of the points (nearest zero) thatseparate a segment with end points 0 and m into n equally spaced points. For example, 3/4 is one of the points that divide segment 0,3 into 4 congruent segments. Add 3/4 to itself to get the other three points:
point nearest zero = 3/4
next point to the right = 3/4 + 3/4 = 6/4
next point to the right = 3/4 + 3/4 + 3/4 = 9/4
next point to the right = 3/4 + 3/4 + 3/4 + 3/4 = 12/4 = 3
Since the points are equally spaced the other points that partition the interval 0,m can be obtained by adding m/n to itself n times.
The segment on the half-line with end points 0 and 1 is called the unit interval. This interval (segment) plays a role in some different parts of mathematics. For any natural number n the fraction 1/n is called the reciprocal of the natural number n. Every natural number has a reciprocal. Its numerator is always 1. Examples of reciprocals are
All the reciprocals of natural numbers are always in the unit interval. The numbers 0 and 1/3 form endpoints of a small segment. This segment can be added to itself to give a longer segment 0, 2/3, so
======================
Although zero is not a natural number, the line segment from zero to 1 (also called unity) is called the unit interval. This interval (segment) plays an important role in some different parts of mathematics including this section. Any collection of distinct points in the interior of the unit interval partition (divide) the interval into pieces which are really smaller segments.. Of interest here are collections of equally spaced points. Then the smaller segments joining adjacent points all have the same length. (In plane geometry there is a construction that divides a segment into any number of congruent smaller segments. Click here to see this construction.)
Since the end points are 0 and 1, any internal points of the unit interval will be located by the new numbers which are between 0 and 1.
There is one internal point that divides the unit interval into 2 congruent segments. That point is located by the fraction 1/2.
There are two internal points that divide the unit interval into 3 congruent segments. Those points are located by the fractions 1/3 and 2/3.
There are three internal points that divide the unit interval into 4 congruent segments. Those points are located by the fractions 1/4, 2/4, and 3/4.
A pattern is being established here. Let n equal the number of congruent segments.
There are n-1 internal points that divide the unit interval into n congruent segments. The endpoints of those congruent segments are points located by the fractions 0, 1/n, 2/n , 3/n, ..., (n-1)/n, 1. It seems natural that 0 = 0/n and 1 = n/n. So
Because segments can be added by placing them end-to-end in a straight line,
2/3 = 1/3 + 1/3
2/4 = 1/4 + 1/4, 3/4 = 1/4 + 1/4 + 1/4
2/5 = 1/5 + 1/5, 3/5 = 1/5 + 1/5 + 1/5, 4/5 = 1/5 + 1/5 + 1/5 + 1/5
In general,
2/n = 1/n + 1/n, 3/n = 1/n + 1/n + 1/n, ... m/n = 1/n + 1/n + ... + 1/n (1/n appears m times).
The numbers 1/1, 1/2, 1/3, ..., 1/n, ... are called reciprocals of 1, 2, 3, ..., n, ... The reciprocal of any natural number n is 1/n.
Let m be any natural number between 0 and n. Then m/n could be any of the fractions: 2/3, 6/7, 4/9, 1234/98765,.... The restriction that m
[1.1] (Positive fractions) A positive fraction m/n is formed by two natural numbers m and n. The number m is called the numerator and n is called the denominator.
Expand the positive fractions to negative fractions by allowing m to be any integer. This means that 0/n = 0.
[1.2] (Rational numbers) The rational numbers are all the positive fractions, all the negative fractions and zero.
[1.1] (Positive fraction) A positive fraction m/n is formed by two natural numbers m and n. The number m is called the numerator and n is called the denominator.
Another consecutive point is located by n/n, but this must be the end point 1. (Later the left end point 0 will be located by 0/n.)
Because segments can be added by placing them end to end in a straight line,
[1.1] (reciprocals) The reciprocal is that quantitiy such that the product n(1/n) = 1 where n is any integer not zero.
This statement implies that zero has no reciprocal. 0 times any quantity = 0, never 1.
[1.1] (reciprocals) The reciprocal of integer n is that quantity x satisfying nx = 1.
[1.2] (Multiplication) Multiplication of a segment by a natural number is accomplished by repeated addition of the same segment. For example, 3(AB) = AB + AB + AB.
The following will be assumed. Drawings can be used to give visual support of them. Here AB, CD EF are segments and m and n are natural numbers.
[1.4] The following laws hold for the arithmetic of segments:
In the following discussions the letters h,k,m,n denote natural numbers, and m/n, h/k denote fractions. The letters x,y,z may denote natural numbers or fractions.
Fractions arise naturally when something whole is broken down into component parts with no loss of content. The union of all the parts brings back the whole something. The whole and its parts can be measured somehow, by weight, volume, number of objects in them, etc. It is of special interest if the measures of all the parts are equal.
[2.1] (Physical concept of a fraction) Suppose the whole of something has measure m (a natural number). The whole is separated into n (a natural number) equal parts. Then each part has measure
The above notation for a fraction is the normal or vertical notation. But more often used in these discussions is the inliine or horizontal notation m/n . Examples: the fractions 7/2, 5/3, and 9/4 are the same as the fractions written just before [2.1].
Geometry may provide more credibility to the existence of numbers that are fractions. In this situation the "whole" is a line segment with an end point at the origin O and the other end point on some point corresponding to some natural number. This segment is to be divided into congruent pieces.
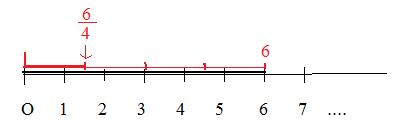
[2.2] (Geometric construction of a fraction) To locate the point that corresponds to the fraction m/n. place a segment of length m on the number half line so that one end point is on the origin and the other end point falls on the point corersponding to m. Perform the geometric construction [1.3] that divides the segment into n equal parts. Locate the part nearest the origin. (Because its length is m/n) the right end point locates the point that corresponds to the number m/n .
For example suppose the fraction 6/4 is given. Using [1.3] divide the segment from 0 to 6 into 4 parts. (See adjacent figure.) The left most part is a segment with the left-hand end point on the origin O and the right-hand end point on the desired point indicated by the vertical arrow.
Up until now a fraction has been represented involving two natural numbers, one above the other. Now let a single letter, say x, y or z, represent a fraction. However, this means that for some natural numbers x = m/n, y = h/k,... etc. Using [2.2] these locate points on the half line. Using [1.1] the sum x + y is possible.
This construction means that any two fractions can be added. It also means that any fraction x may be multiplied by a natural number n because
The above situations (a), (b), (c) can now be expressed respectively in algebraic terms:
Fractions are "invented" to provide solutions to simple equations like those given above.
[2.3] (Algebraic concept of a fraction) Let m and n be natural numbers (positive integers). The symbol
The above notation for a fraction is the normal or vertical notation. But more often used in these discussions is the inliine or horizontal notation m/n . Examples: the fractions 7/2, 5/3, and 9/4 are solutions to the above equations (a"), (b"), (c") respectively.
[2.4] (Equations with unique solutions) Let m and n be natural numbers. There is exactly one solution for x in the equation nx = m.
The existence of fractions means that there is at least one solution for x. Suppose y is also a solution: ny = m. Then nx = ny. By the cancellation law discussed at the beginning of this section, x = y.
[2.5] The product of any fraction and its denominator is equal to the numerator.
If m is the measure of the whole, then the sum of all its parts is (m/n) + (m/n) + ... + (m/n) = n(m/n). This sum must equal the whole which is m.
Example if 4/5 is multiplied by 5 then the result is 4. This statement can be written as 5(4/5) = 4. The absence of an operations sign between the 5 and the fraction 4/5 means multiplication. Unfortunately, widespread is the ambiguity that 5(4/5) means 5 + 4/5, that is some number between natural numbers 5 and 6. In these discussions the addition sign will never be omitted if that is the intention.
[2.6] Every natural number is equal to a fraction with numerator equal to that natural number and denominator equal to 1.
Notation: m = m/1.
In [2.5] replace n by 1.
Two fractions may appear quite different yet be equal. The following statement determines equality by means of multiplication of natural numbers.
[2.7] (Equality of fractions) Two fractions are equal if and only if the product of the numerator of the first and the denominator of the second is equal to the product of the numerator of the second and the denominator of the first.
Note: m and k are on the outside of the inline notation, n and h are on the inside of the inline notation. Remember, product of the outers = product of the inners. 2/3 = 4/6 because (2)(6) [outers] = (3)(4) [inners].
Fractions have been introduced intuitively and not by clear definition. Therefore [2.6] cannot be proven, but can be accepted as a definition of equality. However, a discussion motivating the statement can be made. Multiply both side of the equality m/n = h/k by the product kn. Using [2.5] twice this multiplication clears fractions to give the equality mk = hn. But [2.7] provides a simple proof of the following:
[2.8] (Multiplying both numerator and denominator by the same natural number) Any fraction is equal to the fraction obtained by multiplying the numerator and denominator by the same natural number.
The proof uses [2.7]. The cross multiplication
The equality 2/3 = 2000/3000 is an example of [2.7] where w = 1000.
[2.9] (Equal numerator and denominator) If the numerator and denominator are equal then the fraction is equal to 1.
n/n = (1n)/1n) = 1/1 = 1.
[1.10] (Reciprocals) The reciprocal of a fraction is obtained by interchanging the numerator and the denominator.
It is obvious that the reciprocal of a reciprocal is the original fraction.
[1.11] (Equal reciprocals) The reciprocals of equal fractions are equal fractions.
Using the cross multiplication of [2.7] both fractions produce equal products mk = hn.
[2.10] (Addition of fractions) If two or more fractions have the same denominator then their sum is equal to the sum of the numerators over the common denominator.
The supporting argument starts with the trivial identity m + h + ... + k = m + h + ... + k. Using the distributive lawand the fact that n/n = 1 this means that n[(m/n) + (h/n) + ... + (k/n)] = n(m + h + ... + k)/n . Using the cancellation law for all numbers given at the beginning of this section, the equality follows by cancelling n from both sides of this last equation.
Example: (4/3) + (7/3) = (4+7)/3 = 11/3. Notice that all denominators are 3.
Addition of fractions can still be done if the denominators are different, but the process is more involved. Using [2.8] it is possible to make new denominators the same without changing the values of the fractions. It is always possible, but not always efficient, to use the product of the denominators as the new common denominator.
Example 1: (2/3) + (4/5) . The product of the denominators is (3)(5) = 15. To make the first fraction have denominator 15, multiply numerator and denominator by 5. To make the second fraction have denominator 15, multiply numerator and denominator by 3. The result: (10/15) + (12/15) = 22/15.
Example 2: (7/16) + (9/24). The product of the denominators is 384. Multiply numerator and denominator of the first fraction by 24, and multiply numerator and denominator of the second fraction by 16. Then (168/384) + (144/384) = 312/384.
Example 3: Do the addition of fractions in Example 2 using the least common multiple LCM(16,24) = 48. Multiply the numerator and denominator of the first fraction by 3 and multiply the numerator and denominator of the second fraction by 2 to get (21/48) + (18/48) = 39/48. Multiplying the numerator and denominator of 39/48 by 8 produces the fraction 312/384, the answer in example 2. So the answers in examples 2 and 3 are equivalent. However smaller numbers were involved to do the addition of fractions in this example 3.
Addition of fractions "inherit" some important properties from the addition of natural numbers. The addition of fractions eventually involves the addition of numerators which are natural numbers.
[2.11] (Commutativity) Addition of fractions is commutative.
[2.12] (Associativity) Addition of fractions is associative.
Not only can fractions be added, but also multiplied. Multiplication is much simpler than addition.
[2.13] (Multiplication of fractions) The product of two fractions is a fraction obtained by multiplying the two numerators together and multiplying the two denominators together.
Using [2.5] repeatedly and assuming the associative law it is easy to show that kn[(m/n)(h/k)] = mh and that kn(mh/kn) = mh. Therefore, kn[(m/n)(h/k)] = kn(mh/kn). Using the cancellation law (cancel kn) given at the beginning of this section, the fractions are equal. See also [2.4].
Fractions under multiplication "inherit" some important laws from natural numbers.The multiplication of fractions involve the multiplication of numerators which are natural numbers, and the multiplication of denominators which are also natural numbers.
[2.14] (Commutativity) Multiplication of fractions is commutative
[2.15] (Associaativity) Multiplication of fractions is associative.
[2.16] (Multiplicative identity) The product of 1 and any fraction is that fraction.
Trivially, 1(m/n) = (1/1)(m/n) = 1m/1n = m/n.
[2.17] Reciprocal equals multiplicative inverse) The product of any fraction and its reciprocal is equal to 1.
The product is equal to mn/nm which is equal to 1 by [2.9].
[2.18] (Multiplicative group) The set of all fractions form a group under multiplication:
(a) The product of two fractions is a fraction (closure)
Actually, the fractions form a commutative multiplicative group because of [2.14].
[2.19] (Division) The division of a first fraction by a second fraction is equal to the product of the first fraction and the reciprocal of the second fraction.
Intuitively speaking, fractions form the smallest set of ordinary numbers that has ordinary multiplication defined on it allowing division.
The definition [2.19] means that the fraction m/n may now be interpreted as the division of the natural number m by the natural number n.
The intuitive approach that was used in [2.1] and [2.2] is not used here. It is not meaningful to divide a whole into a negative number of parts. But the algebraic concept [2.3] can be extended to using integers.
[3.1] (A rational number) Let u be any integer and let v be any integer not zero. The symbol u/v denotes a number, called a rational number or simply rational, that satisfies the equation vx = u.
Much of what was said about fractions in the previous section applies to rational numbers. However, the denominator cannot be zero. If v = 0 then vx = u has no solution if u is not zero. On the other hand, there are too many solutions if u = 0. For example, no number x can satisfy 0x = 5 because 0x=0 cannot equal 5. On the other hand any number x satisfies 0x = 0. If a rational number is written with numerator/denominator then it will be assumed that the denominator is not zero.
All the integers can be written as rational numbers with denominators = 1. In particular, 0 = 0/1 and 1 = 1/1.
[3.2] (Equality of rational numbers) Two rational numbers u/v and t/w are equal if and only if the cross product uw = tv is true.
[3.3] From [3.2] come the following identities:
(a) In a rational number, if both the numerator and denominator are negated, then the new number is equal to the old number.
[3.4] (Addition of rational numbers) If two or more rational numbers have the same denominator then their sum is equal to the sum of the numerators over the common denominator.
The sum of a rational number and the rational number obtained by negating the numerator is zero. (u/v) + (-u/v) = 0. This means that (-u)/v is the additive inverse of u/v. So (-u)/v = -(u/v). Notice that u/(-v) is also an additive inverse, because it is equal to (-u)/v. This means that a negative sign can be in three places, before the entire rational number, before the numerator or before the denominator. These statements introduce the negative fractions.
[3.5] (Subtraction of rational numbers) If a rational number is to be subtracted from another rational number and they have the same denominator then subtract the numerator of the number being subtracted from the numerator of the other rational number and the difference is placed over the common denominator.
[3.6] (Multiplication of rational numbers) The product of two rational numbers is a rational number obtained by multiplying the two numerators togther and multiplying the two denominators together.
[3.7] (Division of rational numbers) One rational divided by a second rational number not zero is obtained by multiplying the first number and the reciprocal of the second number.
[3.8] (Division of integers) A rational number is equal to one integer (numerator) divided by another non-zero integer (denominator).
If u is divided by v, then u/1 is divided by v/1 which is equal to the product (u/1)(1/v) = u/v. This assumes that v is not zero.
[3.9] (Absolute value) The absolute value of a rational number is the same number if that number is not negative, and is the negative of that number if that number is negative.
It is not too difficult to see that the arithmetic average (x + y)/2 of two points x and y on the number line is between the two points. If x and y are rational numbers then their average is also a rational number. This means that no matter how close x and y are to each other, another rational number z equal to the average of x and y is between x and y. Intuitively speaking, the set of all rational numbers is, in some sense, a dense set.
An odd fact is that there are just as many rational numbers as integers, even though the integers are part of the rational number system. This oddity is due to the unintuitive nature of infinite collections. A discussion of this fact needs more algebraic "tools" such as the one-to-one function described in a later volume.
[4.1] (Real numbers) A real number is a number with a decimal representation.
This means that all rational numbers are real numbers. However, the decimal representations of fractions like 1/3 exist but are impossible to write out completely because they are infinite: 1/3 = .333333.... The use of .... means that a recognizable pattern can be determined and extended from the listing of digits before .... .
Many decimal representations have recognizable patterns, namely the representation has adjacent blocks of the same digits after the decimal point. For example 1/7 = 0.142857142857142857142857142857... , an infinite decimal representation in which the repeating block is 142857. A more simple example is --4.111111111... in which the repeating block is 1. The integers have repeating adjacent blocks of 0 after the decimal point.
[4.2] (Decimal equivalents of rational numbers) A number is rational if and only if its decimal representation has an infinitely repeating adjacent identical blocks of digits.
Implied here is that any block has a finite length. Click here to see a supporting discussion of this statement.
There is a hint here that there exist decimal representations without repeating blocks. It is possible to indicate representation that may seem artificial, but nevertheless is valid: 0.101001000100001000001..... The pattern here is to include an increasing number of zeros between ones. Whatever number it is, it cannot be a fraction by [4.2], because there is no repeating blocks of digits.
[4.3] (Irrational numbers) There exist real numbers that are not rational.
They are called irrational numbers. Another example of an irrational number is the square root of 2, written sqrt(2) in horizontal notation. It is impossible to show that there is no repeating blocks of digits. Instead the proof is indirect by assuming that sqrt(2) = fraction and getting a false result from this assumption. Click here to see a proof that sqrt(2) is not a rational number. More examples of irrational numbers are sqrt(3), sqrt(5), cube root of -7, π, sin 10°, log 3, although the proofs of the irrationality of the last three are more difficult and are beyond the scope of this chapter.
The point on the number line corresponding to sqrt(2) can be located by constructing the diagonal of a 1x1 square, and copying the diagonal segment onto the positive number half-line with one end at the origin O. The other end point locates the desired point.
Although on the number line the points located by the rational numbers are dense, the points do not completely cover the number line. In fact, it is possible to find points located by irrational numbers between points located by any two rational numbers. The following axiom answers yes to the question, "taken together do all the points located by rational and irrational numbers cover completely the number line?"
[4.4] (Axiom of complete correspondence between the real numbers and points on the number line) Every real number locates a unique point on the number line. Any point on the number line can be located by a unique real number.
It can be shown that there are more irrational numbers than rational numbers. The discussion of this fact is beyond the scope of the present volume.
In the next chapter the number system is again expanded. Some of the new numbers cannot locate points on the number line because it is already covered by points of all real numbers. Those new numbers do locate points elsewhere and are called "imaginary". In contrast the numbers discussed in this section are called "real."
================
The number line is consider solid, no breaks or interruptions in it. This is also true of the unit interval. The end points already have numbers 0 and 1 assigned to them. It is desirable to assign new numbers to some points inside the unit interval. Since the interval is on the positive side of the number line, the numbers locating any
================
It all starts with reciprocals.
Recall the number line on the right side of zero (origin). Do not include zero. The part of the line joining zero to unity (1) is called the unit interval. There are points on this uknit interval and numbers to locate them. For example, the midpoint half way between 0 and 1 is located by the fraction 1/2. The midpoint divides the unit interval into 2 congruent line segments.
There are two points that divide the unit interval into 3 congruent parts. The two points are located by the fractions 1/3 and 2/3.
There are three points that divide the unit interval into 4 congruent parts. The three points are located by the fractions 1/4, 2/4, and 3/4.
A pattern is being established here. Let n be any natural number larger than 1.
There are n-1 points that divide the unit interval into n congruent parts. The n-1 points are located by the n-1 fractions 1/n, 2/n, ..., (n-1)/n
2/3 = 1/3 + 1/3
2/4 = 1/4 + 1/4, 3/4 = 1/4 + 1/4 + 1/4
2/5 = 1/5 + 1/5, 3/5 = 1/5 + 1/5 + 1/5, 4/5 = 1/5 + 1/5 + 1/5 + 1/5
In general,
2/n = 1/n + 1/n, 3/n = 1/n + 1/n + 1/n, ... m/n = 1/n + 1/n + ... + 1/n (1/n appears m times).
The numbers 1/1, 1/2, 1/3, ..., 1/n, ... are called reciprocals of 1,2,3, ..., n, ... The reciparocal of n is 1/n where n is any natural number.
================
In plane geometry there is a construction for dividing a line segment into n congruent parts, where n is any natural number. Click here to see the construction.) The segment with endpoints 0 and 1 on the numberline has special importance and is called the unit interval. It can be partitioned into n contruent parts. The adjoining figure shows the unit interval divided into n=5 contruent parts. The new point closest to 0 is the point located by the fraction 1/5, which is the reciprocal of 5. This same method of separating the unit interval into equal parts will locate points corresponding to 1/2, 1/3, 1/4, .... which are reciprocals of 2,3,4,... .
By adding the segment with end points 0 and 1/2 to itself, the whole unit interval is covered.
By adding the segment with end points 0 and 1/3 to itself so that here are three segments, the three segments cover the entire unit interval.
By adding the segment with end points 0 and 1/4 to itself so that there are four segments, then the four segments cover the entire unit interval
.
Arithmetically,
1/2 + 1/2 = 1
1/3 + 1/3 + 1/3 = 1
1/4 + 1/4 + 1/4 + 1/4 = 1
In general, the sum
1/n + 1/n + ... + 1/n (where 1/n appears n times) = 1
The statement is also true for negative integers.
The statement implies that 1 is its own reciprocal. Also -1 is its own reciprocal. All other reciprocals are not integers (there are no integers between 0 and 1).
The following is a more technical definition.
====================
These two number systems will be developed in intuitive ways using geometry, outlined in section 1, to provide visual support in some places. More rigorous developments can be found elsewhere outside these volumes.
Section 1 Some geometric arithmetic of line segments
In this section some simple geometric constructions are described involving addition of segments and special forms of multiplication and division.
[1.1] (Addition of segments) Simple plane geometry provides a method for addition of parallel segments: place them end-on-end. To add segments AB, CD, EF (Fig 1) together, copy CD so that C falls on B. Then copy EF so that E falls on D (Fig 2). The copies stay parallel to their original segments. The resulting longer segment
AF = AB + CD + EF. (Fig 2)
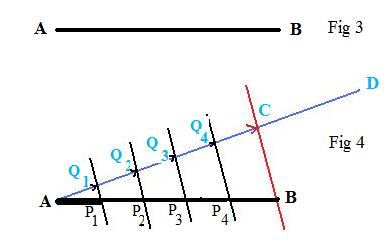[1.3] (Division) Division of a segment by a natural number can be done by a geometric construction involving parallel lines.
GIven segment AB, to divide it into any number of equal parts (segments). The figure shows 5 equal parts.
Through A draw an auxiliary line AD. On this line mark a point Q1 different from A. Mark off the desired number, in this case 5 by adding AQ1 to itself enough times to locate a point C: 5(AQ1) = AC. Draw a line through C and B. Draw lines through points Q1, Q2, Q3, Q4 parallel to the line through C and B. These new lines intersect segment AB in equally spaced points P1, P2, P3, P4 which determine equal parts (segments) on AB.
Note: of special interest will be end point P1 of the left most part AP1.
(a): Addition is commutative: AB + CD = CD + AB
(b): Addition is associative: (AB + CD) + EF = AB + (CD + EF)
(c): Multiplication is right distributive: n(AB + CD) = n(AB) + n(CD)
(d): Multiplication is left distributive: (m + n)(AB) = m(AB) + n(AB)
(e): 1(AB) = AB
(f): If two congruent segments are each separated into the same number of equal parts, then all the parts of both segments are congruent.
Section 2 Fractions
In this section the half-line of the number line will play an important role. The negative part will be ignored. The result is the positive number half line. In this section it will be named simply half line.The origin O will be used only as an anchor for end points of line segments so that the number 0 (zero) will not be used in this section. In this section points other than only those located by natural numbers will be considered. Fractions will locate them. Because of [1.4] it can be assumed that all numbers discussed in this chapter obey the commutative, associative, and distributive laws. Also, because of [1.4f] the cancellation law holds:
Three examples demonstrate these conditions:
(a) A 7 pound sack of salt is divided into 2 smaller but equal sacks.
(b) A board of length 5 feet is sawed into 3 pieces of equal length.
(c) 9 gallons of water in a larger container are poured equally into 4 smaller containers.
The system of integers does not always allow the exact measure of what is in the parts. The best that can be said for the above situations are the following approximations respectively:
(a') In each smaller sack there is between 3 and 4 pounds of salt.
(b') The length of each smaller board is between 1 and 2 feet.
(c') The amount of water in each of the smaller containers is between 2 and 3 gallons.
Numbers of a new kind are to be "invented" to give exact answers. The new numbers will include
(a") Let x = the amount of salt in either smaller sack. Then 2x = 7.
(b") Let y = the length of the smaller piece of board. Then 3y = 5.
(c") Let z = the amount of water in any of the smaller containers. Then 4z = 9.
The left sides of these equations expresses the sum of the measures of all the component parts. The right side expresses the measure of the whole. The solutions x, y, and z denote the unknown measures of any of the parts.
Notation: n(m/n) = m.
Notation: (m/n) = (h/k) if and only if mk = hn.
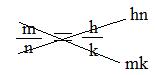
For the normal notation, a large X can be made: the product of natural numbers along one arm of the X is equal to the product of natural numbers along the other arm of the X.
Notation:
Notation: n/n = 1
Notation: The reciprocal of m/n is n/m.
Example 1: The reciprocal of 2/3 is 3/2.
Example 2: The reciprocal of 5 is 1/5 because 5 = 5/1. The reciprocal of m is 1/m. Every natural number has a recirpocal.
Notation: if m/n = h/k then n/m = k/h.
Notation:
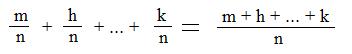
Notation: (m/n) + (h/k) = (h/k) + (m/n).
Notation: [(m/n) + (h/k)] + (p/q) = (m/n) + [(h/k) + (p/q)].
Notation:
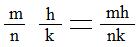
Notation: (m/n)(h/k) = (h/k)(m/n).
Notation: [(m/n)(h/k)](p/q) = (m/n)[(h/k)(p/q)].
Notation: (m/n)(n/m) = 1
(b) Multiplication is associative
(c) 1 is the identity
(d) Every fraction has an inverse, namely, its reciprocal.
Notation: (m/n) divided by (h/k) = (m/n)(k/h).
Section 3 Rational numbers
The term "rational" comes from the term "ratio", which is another way of saying "divided by." In the previous section factions were introduced as numbers having numerators and denominators that are natural numbers. In this section integers, positive, zero and negative may be used, not just natural numbers (positive integers). As a result rational numbers are made up of positive fractions (introduced in the previous section), zero and negative fractions. Many statements here are extensions of corresponding statements in the previous section. Many of the supporting arguments are also similar to those in section 2. Therefore, many statements given in this section will not have supporting arguments. The letters m,n,h,k are still natural numbers but the letters t,u,v,w will be used as integers in this section.
Notation: u/v = t/w if and only if uw = tv.
(-u)/(-v) = u/v.
(b) In a rational number, if the numerator is negated then that number is equal to the number in which the denominator is negated
(-u)/v = u/(-v).
Notation: (u/v) + (w/v) + ... + (t/v) = (u + w + ... + t)/v .
Notation: (u/v) -- (w/v) = (u -- w )/v .
Notation: (u/v)(t/w) = (ut)/(vw) .
Notation: u/v divided by t/w = (u/v)(w/t).
The rational numbers form a commutative additive group, and a commutative multiplicative group without zero. The two groups are connected by a distributive law. Such a system is called a field. Intuitively speaking, it is the smallest field of odinary numbers with ordinary operations of addition and multiplication.
Notation: u divided by v = u/v.
.
Notation: |u/v| = |u|/|v|.
Section 4 Real numbers
It is assumed that the reader recognizes the decimal representation of numbers. The natural numbers 1,2,3,... can be represented as 1.0, 2.0, 3.0, ... although more zeros can be attached, 1.000000, 2.00000000, 3.0000000000, still representing the same natural numbers. Every fraction has a decimal equivalent by dividing the denominator into the numerator with its decimal representation. For example, 4/5 = 0.8 because dividing 5 into 4.0 produces 0.8. Another example is 3/8 = 0.375, obtained by dividing 8 into 3.000. The symbols 0,1,2,3,4,5,6,7,8,9 used to denote the decimal representations are called "digits.". The negative numbers have negative decimal expansions. The following is an "intuitive definition", to give a simple place to start this section. To give an "exact definition" of all real numbers is beyond the scope of this chapter.