Section 2   Multiplication of Natural Numbers

The natural numbers indicate how many repetitions of anything is involved.    3 apples   means    apple,apple,apple.   Using the physical method for finding sums, It is easy to find the sum 4 + 4 + 4. Into an empty bag, add 4 objects, then add 4 more objects, and finally add 4 more objects. Count the total number of objects in the bag. 12 of course. Found was the product 3x4.

[2.1a] (Physical method of finding a product of two natural numbers) To find the product nm, into an empty bag add m objects and do the adding n times. The product is equal to the total number of objects now in the bag.

The first (dark black boldface) number in the product is called a coefficient. It indicates the number of times that the second number is added. Actually the second number could be replaced with an algebraic expression w: For example,
  3w   =   w + w + w.
  3(ax + byz)⁵   =   (ax + byz)⁵ + (ax + byz)⁵ + (ax + byz)⁵.

[2.1b] (Algebraic method for evaluating a product*) The product nw of a natural number   n    and a numerical or algebraic quantity   w    is equal to the sum of that quantity   w    repeated n times in the addition process: nw = w + w + ... + w    (Click here to see how math induction [1.1b] can be used to make this definition more exact.) The integer n is called a coefficient of    w.

Finding areas of rectangles by multiplying lengths of adjacent sides suggests a more organized method for evaluating a product of natural numbers. Let the objects being counted small squares. Instead of using repeated addition (linear form) sq sq sq sq + sq sq sq sq + sq sq sq sq and then counting the sq's, use a two-dimensional rectangular form wiith rows of 4 squares under each other, as shown in the adjacent figure, and then count the squares. This suggests that areas of geometric rectangles provide a method to calculate the product of two natural numbers.

[2.1c] (Geometric method for evaluating a product) To find the product   nm   of a natural number n and a natural number m, construct a rectangle with height n and width m. Then count the number of squares (square areas) the rectangle contains.

[2.2] (Commutative law for multiplication of natural numbers*) For any natural numbers n and m,  nm = mn.

(Dual:   for addition:   n + m = m + n)

Mathematical induction can be used to prove this law for natural numbers. However, a simple geometric argument supports it. Draw the rectangle with height m and width n. Then there are mn squares inside the rectangle. Rotate the triangle through 90° Now it is a nm rectangle. The number of squares is the same because the two rectangles are congruent. The figure to the right shows this argument for the product 3x4 = 4x3.

[2.3] (Associative law for multiplication of natural numbers*) For any natural numbers k,m,n,    k(mn) = (km)n.

(Dual:   for addition:   k + (m + n) = (k + m) + n)

Again this law can be proven using mathematical induction. A geometric argument supports it, using a rectangular three dimensional box containing unit cubes whose count = volume. It will not be given here, and the associative law is assumed to be true.

The definition [2.1b] connects multiplication with addition. The following law connects the two operations in a second way.

[2.4] (Distributive laws for natural numbers*) For any natural numbers u,v,n,    n(u + v) = nu + nv.

A rigorous proof can be made using mathematical induction. A simple algebraic argument based on definition [2.1b] and using the associative and commutative laws, provides support:
   n(u + v)
           = (u + v) + (u + v) + ... + (u + v)              [n times]
           = u + u + u + ... + v + v + v       [each letter appears n times]
           = nu + nv.

The number 1 is the smallest natural number. But it also as a special role in multiplication;

[2.5] (Multiplicative identity*) For any natural number n, the product:  1n = n.


In [2.1b] multiplication was introduced as repeated addition. It is possible to have a number repeatedly multiplied by itself. 5²=5x5 = 25, 10³=1000, w² = ww, w³ = www.

[2.6] (Powers*) The n-th power wⁿ of any natural number m is equal to the product of that quantity repeated n times in the multiplication process: wⁿ = ww...w   where w appears in the multiplication process n times. The integer n is called an exponent on w.

[2.7] (1 As exponent*) w¹ = w.

So [2.7] and [2.5] continue the duality between exponents and coefficients.

[2.8] (Associative law for multiplication*) For any natural numbers u(vw) = (uv)w. (Duality: for addition: u + (v + w) = (u + v) + w.)

[2.9] (Exponential law*)   (c)   (uv)ⁿ = uⁿvⁿ

This law is the dual of the distributive law [2.4]. The proof is similar.

[2.10] (Comparison laws*)
  (a)   if u < v then nu < nv
  (b)   if u > v then nu > nv

The proof of (a) is simple. If u < v then there is a natural number x such that v = u + x. Multiply both sides of this equation by n to get nv = nu + nx. Since nx is a natural number nu < nv. The same argument can be made for part (b).

[2.11] (Cancellation law*)
nu = nv implies u = v

The argument for this law directly supports the contrapositive: if u is not equal to v, then nu is not equal to nv.
If u is not equal to v, then u < v or u > v. If u < v then nu < nv by [2.10a], which means that nu is not equal to nv. Similarly if u > v then nu > nvby [2.10b], which also means that nu is not equal to nv.

Since n is a natural number then it cannot be zero. In the next section about integers, this condition n not equal to zero will be explicitly stated. An argument supporting [2.11] will be supplied there.
The use of the commutative law can be used to prove that [b] follows immediately from [a].

Addition and multiplication combine two numbers to produce a sum and product respectively. They are called binary operations. A binary operation combines any two things from a collection and produces a single quantity that is in that same collection (closure). The commutative and associative laws can be stated as
                                              u o v = v o u                                                [commutative law]
                                     u o (v o w) = (u o v) o w                                       [associative law]
where o may be replaced by either the addition or multiplication symbol. In most systems that the reader may encounter, the associative law will hold true. But in some systems the commutative law may not hold true. Discussed later in this volume are systems of functions, and in other volumes matrices, and quaternions, all of which are not in general commutative. It is customary to write an operation that is not commutative as multiplication.

If a product is equal to the multiplication of two or more natural numbers, then each of those natural numbers is called a factor or divisor of the product. The natural number 3 is a factor of 12 because 12 = 3x4. But 5 is not a factor of 12. Why? Because there is no natural number that can be placed inside ( ) to make the expression 12 = 5x( ) become a true equation. If 2.4 is placed inside ( ), the expression becomes a true equation, but 2.4 is not a natural number.

The natural number n is a factor of a number m if there is a natural number that can be placed inside ( ) to make the expression m = n x ( ) become a true equation. A much better way of expressing this is as follows where y = ( ):

[2.12] (Factors and divisors*) A natural number n is a factor or divisor of a natural number m if and only if there exists a natural number y satisfying the equation m = ny    [nk = product of n and y].
Notation: n | m   means   n is a factor of m.

By algebra y = m/n (quotient). However, this fraction which indicates ordinary division, may or may not equal a natural number. The fraction 1212/5 is not. Therefore 3 is a factor of 12, and the fraction 12/3 = 4 is the other factor of 12. But 12/5 is not equal to a natural number.

[2.13] (Test for factor by division) The natural number n is a factor of a natural number m if the fraction m/n is equal to a (whole) natural number. If it is equal, then that natural number is equal to the other factor of m. (The two factors may be equal.) Logically, the statement [2.13] is out of place, because division has not yet been defined. But this premature use of fractions here makes the process of determining whether or not a natural number is a factor very simple and clear.
For a natural number to be a perfect square, the two factors, by definition, are equal. For examp[le, 81 = 9x9. The fraction 81/9 = 9. Therefore, 9 is a factor of 81 and 9 is the "other" factor.
The division m/n can be done more conveniently by electronic devices, such as a calculator.

[2.14] (Multiples*) A natural number m is a multiple of a natural number n   iff   n is a factor of m.

For example,

A duality exists between factor and multiple:     7 is a factor of 21   21 is a multiple of 7.

Sometimes for a given natural number all of its factors are wanted. These can be given in a list { }. One reliable but laborious way to get this list for a natural number m is to evaluate all of the fractions

For any natural number there is a (finite) list of all the natural numbers that are its factors.
    The list of all factors of 12 is   {1,2,3,4,6,12}
    The list of all factors of 40 is   {1,2,4,5,8,20,40}
    The list of all factors of 48 is   {1,2,3,4,6,8,12,24,48}
    The list of all factors of 17 is   {1,17}

Click here to see some facts that reduce the number of fractions to be tested for complete division.

There may be much computation even after removal of some of the fractions because many fractions may remain to be tested for complete division. especially if the natural number is very large, such as 9473651. And done by hand or calculator it is easy to miss some of the factors. Click here to find a computer program to produce this list of all the factors of a natural number (within the capacity of the machine, often less than or equal to 4 294 967 291).

By [2.5], 1 is a factor of every natural number. Also every natural number n is a factor of itself. These two numbers, 1 and n must be in every list of all factors. For any natural number n, the numbers 1 and n are called trivial factors of n. Factors not trivial are called non-trivial. In the above lists the non-trivial factors are in darker boldface.

[2.15] (Primes*) A prime is a natural number that is larger than 1 and that has only trivial factors. A number larger than 1 but not a prime is called composite.

The following is a list of all the primes that are less than 100..

It is convenient to use a computer to show that the natural number 2 147 483 647 is a prime. In fact it is the largest positive prime in many computer systems.

The ancient Greek geometer Euclid proved that the list of all primes is infinitely long. Another ancient Greek, Eratothenes, discovered a method, called a sieve, for finding all primes. Click here to see a discussion of this method. No algebraic formula has yet been invented for finding all the primes. It seems that the primes are distributed randomly among all the natural numbers.

The numbers 42 and 87 are composite. They are not in the list (&). For convenience later, 1 is not allowed to be a prime..

Intuitively speaking, a composite natural number may be "broken down" into smaller pieces, its factors. The composite number 45 can be broken down into factors 9 and 5. A prime cannot be broken down into smaller pieces. The number 17 has only trivial factors, and cannot be broken down into smaller pieces.

Sometimes the factors can be broken down.   45 = 9 x 5 but 9 can be broken down into 3 and 3, so that 45 = 3 x 3 x 5. None of these factors can be broken down further. The number 45 has been broken down into primes and the "breaking down" process stops there. Using exponents, 45 = 3² x 5.

This process of breaking down factors into smaller factors to get prime factors is based on the following theorem:

[2.16] (Transitive property of being a factor*) If a first natural number is a factor of a second natural number, and that second natural number is a factor of a third natural number, then the first natural number is a factor of the third.

For example, 3 is a factor of 12, and 12 is a factor of 84, so 3 is a factor of 84. Click here to see a simple proof of this theorem.

The following is an immediate result of [2.16]

[2.17] (*) If a natural number is not a factor of a second natural number, then no multiple of the first number can be a factor of the second number.

For example 2 is not a factor of 99, then 4,6,8,10,... cannot be factors of 99.

Non-trivial factors of a given natural number are smaller than that number. Usually the smaller the number the easier it is to find its factors, which in turn will be factors of the original natural number. For example it is obvious that 10 is a factor of 560. But 2 and 5 are factors of 10. Therefore 2 and 5 are factors of 560. Dividing 10 into 560 produces 56 which is a factor of 560. Since 56 = 8x7, and 2 is a factor of 8, the prime factors of 56 are 2 and 7. Therefore the list of all prime factors of 560 is {2,5,7}. This discussion shows a method for finding all the prime factors of a natural number.

Every breaking down a natural number into prime factors will produce the same prime factors. But 560 is not equal to the product of its prime factors; because there are composit factors. for example 56.. However 560 = 16x5x7 = 2⁴x5x7. Click here for a brief discussion of complete factorization of any natural number.


Besides the collection N of all natural numbers, there are other collections of natural numbers, some of which are useful in reality and in later discussions. The list of all even natural numbers

In general each number in the list N may be multiplied by any natural number k to produce a new list kN of all multiples of the number k:

[2.18] (Addition of numbers with a common factor) Any common factor of two (or more) natural numbers is a factor of their sum.

Suppose k is a common factor of m and n. Then by definition   m = ku   and   n = kv   for some natural numbers u and v. Now a form of the distributive law is   ku + kv = k(u + v).   Therefore,

The list kN is closed under addition. A collection of numbers not closed under addition would be a defective system in many cases. For example, in the list {4,7} there are just two numbers. It is not closed under addition, because 4+7 = 11 and 11 is not in the list. In fact, the only collections of natural numbers, closed under addition, are all the multiples of some natural number. This fact will be discussed in the next section.

Suppose the coefficients in the collection kN become exponents:

In the collection of powers of some natural number, the product of any two natural number is back in the collection. So the colllection is closed under multiplication.

A collection of numbers not closed under multiplication would be a defective system in many cases. If only 4 and 7 were in some collection, then that collection of just two numbers is not closed under multiplication, because 4x7 = 28 and 28 is not in the collection. In fact, the only collections of natural numbers (having some natural number not 1), closed under multiplication, are all the powers of some natural number.


The following are three equivalent fractions:
To get the second fraction, divide both the numerator 12 and denominator 40 of the first fraction by 2. Toget the thrid fraction divide the numerator 6 and the denominator 20 of the second fraction by 2.

The following statements are copies from above:
    The list of all factors of 12 is   {1,2,3,4,6,12}
    The list of all factors of 40 is   {1,2,4,5,8,20,40}
The factor 2 is in both lists. The factor 4 is also in both lists. To get the third fraction directly from the first, divide both the numerator 12 and denominator 40 of the first fraction by 4.

A factor (or divisor) is common to two or more lists of factors if it is in all the lists. A fraction remains equal if both its numerator above and denominator below are divided by a common factor. Those two divisions produce natural numbers because the division involves factors.

The list of common factors of 40 and 60 is {1,2,5,10,20}. The highest common factor is 20. Use it to divide both numerator 40 and denominator 60 of the first fraction to get the second fraction:
The reader can make the lists of all factors of 40 and of 60, and verify that the natural number 20 is the largest factor in both lists.

[2.19] (Highest Common Factor*) The highest common factor (or greatest common divisor) of two natural numbers is the largest factor that is in both lists of all factors.
Notation:   hcf(u,v) = highest common factor of natural numbers u and v.
Other notation:   gcd(u,v) is the greatest common divisor of natural numbers u and v.
Click here for a technical definition of hcf.

hcf(12,40) = 4.
From
    The list of all factors of 40 is   {1,2,4,5,8,20,40}
    The list of all factors of 48 is   {1,2,3,4,6,8,12,24,48}
it is seen that hcf(40,48) = 8.
The reader can verify:   hcf(8,10) = 2,   hcf(15,9) = 3,   hcf(12,12) = 12,   hcf(8,27) = 1.
Without the laborious work of finding and listing all factors, the following can be stated as true:   hcf(28459,28459) = 28459,   hcf(1,25943) = 1   hcf(10,20) = 10.
It is easy to expand [2.15] to define the hcf of more than two natural numbers: hcf(4,6,26) = 2.

1 is a factor of every natural number. It may happen that it is the only number in both lists of all factors of two natural numbers, such as 8 and 27:     hcf(8,27) = 1.
   the list of all factors of 8 = {1,2,4,8}
   the list of all factors of 27 = {1,3,9,27}

[2.20] (relatively prime*) Two natural numbers are relatively prime iff their greatest common factor is 1.

A fraction is (expressed) in lowest terms if its numerator and denominater are relatively prime.

The fraction 8/27 is expressed in lowest terms. The fraction 4/6 is not expressed in lowest terms because hcf(4,6) = 2. If the numerator 4 and the denominator 6 is divided by 2, then the equivalent fraction 2/3 is expressed in lowest terms. Division of numerator and denominator of a fraction by any common factor larger than 1 produces an equivalent fraction with smaller numerator and denominator.

lowest terms For fraction u/v, if the numerator u and denominator v are both divided by hcf(u,v) the an equivalent fraction will be obtained that is expressed in lowest terms. This statement is based on the following.

[2.21] (Lemma) If both of any pair of natural numbers are divided by their highest common factor then the quotients are relatively prime natural numbers.

For example, hcf(15,25) = 5. 15/5 = 3, 25/5 = 5, and 3 and 5 are relatively prime. Another example, hcf(60,70) = 10. 60/10 =6, 70/10 = 7. 6 and 7 are relatively prime. Also,
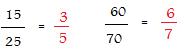
The fractions are shown with their equivalent fractions that are in lowest terms.

Click here for a discussion supporting the lemma.


The definition [2.15] of hcf does not provide an efficient method (algorithm) for computing it by hand. The following fact[2.18] is a basis for a more efficient method for calculating the hcf. Recall that |u - v| means u - v or v - u, so that |u - v| will give a natural number as a difference. (See [1.14] in the previous section.)

[2.22] (*) If a natural number k is a factor of two (unequal) natural numbers u and v, then k is a factor of their (absolute) difference |u - v|
In symbols:    if k | u and k | v    then     k   |   |u - v|.

For example, 3 is a factor of both 24 and 18. Therefore 3 is a factor of 24 - 18 = 6. (Choose the subtraction 24 - 18, and not 18 - 24.)   Since 7 is a factor of both 14 and 56 it is a factor of |14 - 56| = 42.

[2.23] (*) Two facts are critical for a first more efficient method for finding the hcf of two natural numbers:
  (a) The highest common factor of a natural number and itself is that natural number. hcf(u,u) = u.
  (b) The highest common factor of two different natural numbers is not changed if the larger number is replaced by their difference.
If u>v then hcf(u,v) = hcf(u-v,v);    if v>u then hcf(u,v) = hcf(u,v-u).

[2.24] (Subtraction algorithm for finding hcf*)
Given two natural numbers u,v. To find the hcf(u,v).
 (a): if u = v, then then u is the highest common factor. Exit algorithm.
 (b): if u and v are unequal,
    (b₁) if u>v then replace u by u-v: hcf(u,v) = hcf(u - v, v);
    (b₂) if v>u then replace v by u-v: hcf(u,v) = hcf(u,v - u ).

For example,
  hcf(40,60)
    = hcf(40,60-40)    (by b₂)
    = hcf(40,20)
    = hcf(40-20,20)    (by b₁)
    = hcf(20,20)
    = 20                    (by a).
Click here for another example of finding the hcf.

Click here for a computer program to execute the algorithm [2.20] and let the computer do the computation. But if the reader does the computation for hcf(1000,5) = 5 he will discover a type of inefficiency of [2.20]. Later another much more efficient alborithm will replace algorithm [2.20].


In [2.14] a multiple was defined: if u is a factor of w, then w is a multiple of u. This reciprocal relationship is a duality between "factor" and "multiple." For many of the facts about factors there are dual facts about multiples. The dual statement of [2.16] can be obtained by replacing every appearance of "factor" by the word "mulltiple" to obtain another fact:

[2.25] (Transitive property of being a multiple*) If a first natural number is a multiple of a second natural number, and that second natural number is a multiple of a third natural number, then the first natural number is a multiple of the third.

The dual of "No factor of a natural number is greater than that natural number" is "No multiple of a natural number is less than that natural number." The duals of some true statements are false. One must be careful in forming dual statements of true statements. The dual of "each natural number has a finite number of factors" is "each natural number has an infinite number of multiples." A simple way to get all the multiples of any natural number is to multiple all the natural numbers by that number.

A multiple is common to two or more lists of multiples if it is in all the lists.
The list of all multiples of 4 is {4,8,12,16,20,24,28,32,36,40, ...}
The list of all multiples of 6 is {6,12,18,24,30,36,42, ...}
The list of all common multiples of 4 and 6 is {12,24,36,... }

[2.26] (Least Common Multiple*) The least common multiple of two natural numbers is the smallest multiple that is in both lists of all multiples.
Notation: lcm(u,v) = least common multiple of natural numbers u and v.
Click here for a technical definition of lcm.

Comparing the definition [2.26] of lcm with the definition [2.19] of hcf, it is obvious that the definitions are duals of each other.
lcm(4,6) = 12.

Recall the addition of fractions. To add two fractions it is necessary to have the same denominators. The numerator and denominator of each fraction can be multiplied by the same factor to make denominators equal. Therefore, the denominators must be a common multiple of the original denominators.
In the adjoining figure, 4 and 6 are the original denominators. Their product 24 is a common multiple. Multiply the numerator and denominator of the first fraction by 6 and multiply the numerator and denominator of the second fraction by 4 to get new fractions 18/24 and 4/24. These fractions are equavilent to the original 3/4 and 1/6, and can be added to get 22/24. Reduced to lowest terms the final fraction is 11/12.
In the second row of the figure the hcf(4,6) =12 is used as the common denominator. Less computation is needed there.

There is a connection between hcf and lcm:

[2.27] (*) The product of the hef and lcm of two natural numbers is equal to their simple product:
hcf(u,v) x lcm(u,v) = u x v.

hcf(4,6) = 2;   lcm(4,6) = 12.     2 x 12   =   4 x 6.

There is no algorithm supplied here to find directly the lcm of two natural numbers u,v. The lcm(u,v) can be found by computing the hcf(u,v) and then evaluating the quotient in lcm(u,v) = uv/hcf(u,v). In short:    lcm = product/hcf . lcm (8,20) = 8 x 20/hcf(8,20) = 160/4 = 40. Since the hcf is a factor of both 8 and 20, it is possible to divide the hcf into the larger, namely 20 to get 5. lcm(8,20 = 8 x 20/hcf(8,20) = 8 x 20/4 = 8 x 5 = 40. This procedure may avoid some large numbers.

The proof of [2.27] uses the technical definitions of hcf and lcm and a repeat use of logical implication. Click here to see the proof. Another proof uses the complete factorization into powers of primes. That proof is not given.

The the following "lemmas" are actually theorems of lesser importrance, except that they will be used in the next section. The letters u,v,n represent arbitrary natural numbers.

[2.28] (Lemma) If the product of two natural numbers is 1 then those natural numbers each equals 1. If uv = 1 then u = v = 1.

The contrapositive is proven. Suppose v is not 1. Then b > 1. Then by the previous lemma, ab > a. Since a is a natural number, a is at least 1. This means that the product ab >1. This is a denial that ab = 1.
A similar argument can be made for a not being 1.

[2.29] (Lemma*) If two natural numbers are factors of each other, then those numbers are equal. If m | n   and   n | m    m = n.

Given are v = ux and u = vy, for some natural numbers x and y.Replace u in the first equation by vy to get v = vxy. Hence 1v = vxy. By the cancellation law 1 = xy. By a previous lemma, x = y = 1. Therefore u = v.