Additional material
Return to listing of all chapters in this volume

Chapter 2
Open Statements and Quantifiers

Section 1:   Basic ideas about open statements

In these volumes the word object has an arbitrary meaning, and could be a number, a geometric point, a person. A universe is a collection of objects and remains unchanged. The collection serves as a source from which objects may be selected (but not removed) during a discussion. Objects outside a universe will be ignored. Usually the objects in a universe are all of the same type. For example,
N5 = {1,2,3,4,5}   and    N9 = {1,2,3,4,5,6,7,8,9}
are two universes of numbers. Either may serve as a universe in some discussions below. A rectangle may be drawn and the collection of all points inside the rectangle serve below as a different universe. All the people in some country may serve as a universe. If no specific universe is declared the letter U will designate an arbitrary universe.

Using N5 as a universe which numbers in it are less than 2.5? To answer this simple question examine individually each number in N5:

1 is less than 2.5
2 is less than 2.5
3 is less than 2.5
4 is less than 2.5
5 is less than 2.5
This table can be reproduced by substituting each of the numbers in N5 into the expression
(*)         x is less than 2.5             
This gives x the nature of a variable. Numbers like -5,0,6,7,... are outside universe N5 and are not eligible for substitution for x in (*), even though their substitutions would produce meaningful logical statements. Expressions like (*) with variables that can be replaced by objects (numbers) in some universe have special names in discussions of this chapter.

[1.1] (Open statement) An open statement in x with universe U is a form which becomes a logical statement when x is replaced by (the name of) any object in U. That logical statement so produced is called a component of the open statement.

For example, the substitution of 2 for x in the open statement   (*)   produces the component   "2 is less than 2.5".

Since components are logical statements, all components have truth values. The following enhanced table shows them:

1 is less than 2.5      T
2 is less than 2.5      T
3 is less than 2.5      F
4 is less than 2.5      F
5 is less than 2.5      F

Notice that an open statement itself does not have a truth value. It is neither true nor false. The components have the truth values.

The logic studied in these volumes is not concerned with the grammatical aspects of the components, but with their truth values. The truth values from the components may be assigned to all objects in the universe. The open statement (*) makes the following assignments of truth values directly to numbers in N5:

1 T,   2 T,   3 F,   4 F,   5 F
The numbers assigned a T answer the question given above.

[1.2] (Truth set) In the universe of an open statement, the collection of all objects assigned a T by the open statement is called the truth set of the open statement.

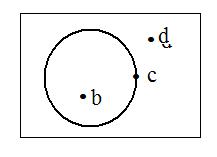
For an example of direct assignments, suppose the universe U is the interior of the rectangle in the adjacent figure. A circle is inside the rectangle. The open statement

x is inside the circle
assigns to points b, c, d the following truth values:
b T,   c F,   d F 
The truth set of the open statement is the interior of the circle.

-----

Other variables like y or z may be used in open statements. By substituting the numbers in the universe N5 for y in the open statement
y is less than 2.5
the same five components given above will be reproduced.

-----

Open statements in x may be symbolized by function notation p(x), q(x), r(x),... . The notation
(**)         p(x):   x is less than 2.5
means that symbol p(x) represents the open statement   x is less than 2.5.   The x in p(x) specifies the variable in the open sentence: p(y) deontes the open sentence in y:   y is less than 2.5.   Also replacing the variable by (names of) objects in the universe produces components;:
p(1): 1 is less than 2.5
p(2): 2 is less than 2.5
p(3): 3 is less than 2.5
p(4): 4 is less than 2.5
p(5): 5 is less than 2.5
But the components have truth values. There is no ambiguity in writing
p(1) T,   p(2) T,   p(3) F,   p(4) F,   p(5) F
to show the truth values for each component.

An open statement with universe U is a method for assigning truth values to every object in U. (In volume C that process of assigning those truth values to all objects in U determines a function from U to the collection of truth values {T,F}.)

--------

Usually objects being assigned a T are more important to a discussion than objects being assigned an F. For example, the solution to an equation 2x = 6 is more important than numbers that do not satisfy the equation. In a universe the collection of all objects assigned a T by an open statement is called the truth set of that open statement. (In algebra it may be called a solution set for some equations.) The truth set for the open statement (*) with universe N5 is {1,2}.

It is possible that the truth set of some open statement be the whole universe. Consider the open statement

x is less than 6
with universe N5. It is obvious that all the components of the open statement are true, and that the open statement assigns a T to every number in that universe. An open statement is universally true if all of its components are true (and therefore if every object in its universe is assigned a T). Equations like x + 1 = 1 + x are universally true open statements, and are called identities in algebra.

A similar definition exists for "universally false." However, this situation has lesser importance. An open statement is universally false if all of its components are false (and therefore if every object in its universe is assigned an F). For an example, the equation   2x = 7   is universally false for every number in the universe {1,2,3,4,5}. The equation is never true for any of those numbers. (Fractions are needed.) The truth set of a universally false open statement is said to be empty.

Open statements do not have truth values. But a remark that "an open statement is universally true" does have truth value. It is false if the open statement assigns an F to some object in its universe.

[1.4] (Counterexample) An open statement cannot be universally true if some object in its universe receives an F. That object is called a counterexample to the declaration that the open statement is universally true.

A counterexample is really an exception. Examples

Consider the open statement

x is less than 2.5
with universe N5. It is false to declare that the open statement is universally true, because 4 is in N5 and 4 receives an F because "4 is less than 2.5" is false. Only one counterexample is needed. Other objects may be counterexamples, but usually are not mentioned.

Let the universe be all people in our world. The open statement is "x lives in the USA". This open statement is not universally true because the queen of England is a counterexample.


Section 2:   Quantifying open statements

Quantifiers in this section answer the question "How many objects in the universe are assigned a T by an open statement?" Except for 0 and 1, the exact number of objects is seldom important. For any open statement the answer will be one of the following: "every object", "at least one object", "exactly one object" or "no object."

Some equivalent phrases:
   "all objects", "each object", "any object";
   "one or more objects";
   "at least one object but not more";
   "no objects", "not any object", "not a single object".

Some examples:
  for every integer x,   x + 1 = 1 + x
  for every integer x,   x + 1 is not equal to x
Both of these statements are true. But the following are obviously false:
  for every integer x, x2 = 9
  for no integer x, x2 = 9

Even though an open statement has no truth value, a quantifying phrase before it produces a statement that is either true or false.

[2.1] (Universal quantifiers) A universal quantifier says that an open statement assigns the same truth value to every object in the universe without exception.

[2.1a] (Positive universal quantifiers) A positive universal quanitifier with an open statement says that open statement is universally true.

In English there are different words to express the positive universal quantifiers. All of the following quantified statements say that the open statement p(x) is universally true
  for every x in U, p(x)
  for each x in U, p(x)
  for all x in U, p(x)
  for any x in U, p(x).

It may be convenient to indicate the universe before the variable in the quantifying phrase:
  for all integers x,   x + 1 = 1 + x,           or            for all x in N, x + 1 = 1 + x
  for any triangle x,   x has three sides

[2.1b] (Negative universal quantifiers) A negative universal quanitifier says that an open statement is universally false.

The It is obvious that if no object in the universe receives a T, then the open statement must be universally false. The following statements say that p(x) is universally false:
  for no x in U (in the universe), p(x)
  not for any x in U(in the universe), p(x)

Specific examples of negatively quantified open statements:
  for no triangle x, x has 4 sides
  for no integer x, x + 1 = x

Actually this negative universal quantifier is not the only way to express universal falsehood. The entire expression may be restated with the negative part moved to the open statement itself and the positive universal quantifier is applied:
  for all triangles x, x does not have 4 sides
  for all integers x, x + 1 is not equal to x
And in general:

[2.2] (Saying) an open statement is universally false   is equivalent to (saying)   all of its components are not true.
Notation: for no x in U, p(x)   <-->   for every x in U, ~p(x)

Because of [2.2] negative universal quantifiers like "for no x" are seldom used. In these discussions the term universal quantifier will mean a positive universal quantifer. If used, a negative universal quantifer will be obvious in a quantifying expression.

Be careful with negation and the quantifier "any." Compare the following quantified open statements:

not every number x satisfies x<5,       not any number x satisfies x<5
The first quantified open statement is true, but the second is false. Negating "any" is not the same as negating "every", "each", or "all".
Use     for every x in U, ~p(x)    instead of    not for any x in U, p(x).
Both are universal denials of p(x).

------

In most discussions here the open statements are not universally false. They assign a T to one or more objects in the universe. The number of objects receiving T is not important here, just the fact that at least one object is assigned a T. A new quantifying phrase is needed to express this situation.

[2.3] (Existential quantifier) An existential quantifier says that an open statement has at least one true component (and in the universe at least one object has been assigned a T).
Notation: for some x in U, p(x)     to mean     there exists at least one object in U and that object is assigned a T).

Another notation is "there exists an x in U such that p(x)". Intuitively speaking, a search of the universe U reveals some object that has been assigned a T by an open statement.

In contrast to the (positive) universal quantifiers with the sweeping statement that all objects in the universe, there is another type of quantifier. Intuitively speaking, it "looks over more carefully" the universe for an object with a T.
Examples Let N5 be the universe. Then the open statement "x is less than 3" assigns a T to the number 2. So the quantified exprsssion "there exists an x in N5such that x is less than 3" is true. But the open statement "x is less than 1" is universally false. No object in N5 is assigned a T. So the statement "for some x in N5, x is less than 1" is false.

The existential quantifier may be expressed as follows:
  there exists an x, p(x)
  there exists an x such that p(x)          (a more grammatical expression in English)
  for some x, p(x)

The following are true statements:
  There exists an integer x such that x2 = 9
  There exists a triangle y such that y has a right angle
  For some city z, z has more than a million people in it.
  For some integer w, w + 1 = 1 + w     (compare: for every integer x, x + 1 = 1 + x)

Sometimes it is desirable to indicate that there exists exactly one object receiving a T from an open statement. For example,

2x + 6 = 20
can be solved with exactly one number, and no other. That number is unique. This uniqueness is expressed in the quantifying phrase:
there is exactly one object in the universe receiving a T
This cumbersome statement is usually condensed to
there exists a unique integer x such that 2x + 6 = 20
Similarly, there can be only one president of the USA.
there exists a unique person x such that x is president of the USA
The open statement assigns a T to just one object in the universe. Anly one T. All other assignments are F.

[2.5] (Uniqueness quantifier) The expression

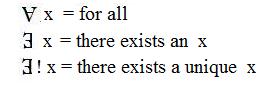there exists a unique object x in U, such that p(x)
is true if and only if p(x) has exactly one true component and all other components are false (exactly one object in U receives a T and all other objects receive an F).

In some works of mathematics and logic there are special symbols used in quantifying expressions. Three are shown in the figure at the right: an upside-down A and a backwards E. They are not used in these discussions for typographical reasons. Instead, the quantifying phrases will be given in English.


Section 3:   Compound open statements

It is possible to form an open statement from one or more open statements with the same universe. For example, if
p(x): x > 3,        q(x): x < 7
and the universe is N9 = {1,2,3,4,5,6,7,8,9} then it is obvious that the numbers satisfying the conjunction
p(x) and q(x):   x > 3 and x < 7
are between 3 and 7, namely 4,5 and 6. The numbers 1,2,3 do not satisfy   x > 3,   and the numbers 7,8,9 do not satisfy   x < 7.

This is an example of a conjunction   p(x) and q(x)   of open statements p(x), q(x).

[3.1] (Compound open statements) Let p(x), q(x) be open statements with a common universe U. The following are basic compound open statements with universe U using logical connectives introduced in chapter 1 of this vollume:
   (a) denial: ~p(x)
   (b) equivalence: p(x) <==> q(x)
   (c) conjunction: p(x) and q(x)
   (d) alternation: p(x) or q(x)
   (e) incompatibility: p(x) is incompatible with q(x)
   (f) implication: p(x) ==> q(x). The open statements p(x), q(x) are called participating open statements in each of the above compound open statements.

These compound open statements are open statements. They have components and assign truth values to all objects in the common universe U. But the truth values assigned to any object depends upon the truth values that the participating open statements assign to that object and the connective joining the participating open statements. In particular consider the conjunction

p(x) and q(x)
Let b be an object in the universe. Suppose that p(x) , q(x) assign a T to object b. That means that both components p(b) and q(b) are true. By rules of conjunction of logical statements the conjunction   p(b) and q(b)   is true. But   p(b) and q(b)   is a component of the open statement   p(x) and q(x) and is true. Therefore
if p(x), q(x) assign a T to an object then the conjunction   p(x) and q(x)   assigns a T to that same object
More briefly,

Table for conjunction   p(x) and q(x)
To any object in the universe:
if p(x), q(x) assign T,T then   p(x) and q(x)   assigns T
if p(x), q(x) assign T,F then   p(x) and q(x)   assigns F
if p(x), q(x) assign F,T then   p(x) and q(x)   assigns F
if p(x), q(x) assign F,F then   p(x) and q(x)   assigns F.

A similar table can be constructed for equivalence.

Table for equivalence   p(x) <==> q(x)
To any object in the universe:
if p(x), q(x) assign T,T then   p(x) <==> q(x)   assigns T
if p(x), q(x) assign T,F then   p(x) <==> q(x)   assigns F
if p(x), q(x) assign F,T then   p(x) <==> q(x)   assigns F
if p(x), q(x) assign F,F then   p(x) <==> q(x)   assigns T.

Because any compound open statement is an open statement, it must assign truth values to every object in its universe. Some compound open statements are universally true. Very important is the situation when that happens with equivalence. Then the above table for equivalence is reduced to the first and last possibilities.
To any object in the universe:
if p(x), q(x) assign T,T then   p(x) <==> q(x)   assigns T
if p(x), q(x) assign F,F then   p(x) <==> q(x)   assigns T.
This forces p(x), q(x) to assign the same truth values to every object in the universe.

[3.2] (Equivalent open statements) Open statements with the same universe are equivalent if and only if they assign equal truth values to every object in that universe.

Actually the term should be "universally equivalent" but it is common to omit the word "universally".

Example 1: The open statements

p(x): x < 3,      q(x): x + 1 < 4
with universe N5 are equivalent because they assign the same truth values to 1,2,3,4,5:
p(1),q(1) TT;   p(2),q(2) TT;   p(3),q(3) FF;   p(4),q(4) FF;   p(5),q(5) FF

Example 2: In the adjacent picture let c be the center of a circle of radius 6. The universe is the collection of all points inside the rectangle. Then the following open sentences are equivalent:

point x is inside the circle,       the distance between points x and c is less than 6
To any point inside the circle TT is assigned and to any point not inside the circle FF is assigned.

It is obvious that two equivalent open statements cannot assign different truth values to any single object in the universe.

In this section discussions concern two open statements that have the same universe. Each assigns truth values to all the objects in that universe. Each object may receive the same truth value from the open statements, or it may receive different truth values. For example, the assignments by   x < 4   to numbers in the the universe {1,2,3,4,5,6,7} are:

1 T, 2 T, 3 T, 4 F, 5 F, 6 F, 7 F.
The open statement   x + 1 < 5   obviously makes the same assignments. Therefore, the open statements "x < 4" and "x + 1 < 5" are related because of the identical assignments of truth values.

[3.1a] (Equivalence of open statements - objectwise) Two open statements with the same universe are (logically) equivalent if and only if they assign the same truth values to each object in the universe.
Notation p(x) <==> q(x)   if and only if   p(x) and q(x) assign the same truth value to each object x in the universe.

Although it is somewhat redundant, tt is instructive to consider the components of these two open statements. Let p(x) and q(x) represent the open statements:

p(x): x < 4,       q(x): x + 1 < 5
Evaluation of all of the components shows logical equivalences:
p(1) <--> q(1) because p(1), q(1) both T
p(2) <--> q(2) because p(2), q(2) both T
p(3) <-->q(3), because p(3), q(3) both T
l(4) <--> q(4) because p(4), q(4) both F
p(5) <--> q(5) because p(5), q(5) both F
p(6) <--> q(6) because p(6), q(6) both F
p(7) <--> q(7) because p(7), q(7) both F
Let U = {1,2,3,4,5,6,7}. Then the equivalence of all the corresponding components of p(x) and q(x) can be stated compactly in the following quantified expression:
for all x in U, p(x) <--> q(x)
It can be read: for all x in U, p(x) is equivalent to q(x).

[3.1b] (Equivalence of open statements - componentwise) Two open statements with the same universe are (logically) equivalent if and only if all their corresponding components are (logically) equivalent.
Notation: p(x) <==> q(x) if and only if   for all x in the universe, p(x) <--> q(x).


Equivalent open statements assign the same truth values to each object. The other extreme is that two open statements assign opposite truth values to each object.

[3.2a] (Universal denial of an open statement - objectwise) An open statement is a universal denial or logical negative of a given open statement if and only if the two open statements assign opposite truth values to every object in a common universe. Notation: q(x) is the logical denial of p(x) if and only if they assign opposite truth values to each object x.

For example, let the universe be {1,2,3,4,5,6,7}. The open statement   x < 4   makes the following assignments of truth values to the numbers in this universe:

1 T, 2 T, 3 T, 4 F, 5 F, 6 F, 7 F.
The open statement   x > 3   makes different assignments:
1 F, 2 F, 3 F, 4 T, 5 T, 6 T, 7 T.
. The pattern is obvious, the open statements   x < 4   and   x > 3   assign opposite truth values to each number in the common universe. In a sense the two open statements completely "oppose" each other with there assignments of truth values.

English provides a grammatical method of negation, involving words like not. If p(x): x is less than 4, then ~p(x): x is not less than 4. Another "safe" method of creating a denial is: ~p(x): it is false that x is less than 4, which reflects the tilda (~) notation. Using this notation,

q(x) is a logical denial of p(x) if and only if   q(x) <==> ~p(x).

Switching the direction of an inequality sign does not form a (complete) negative of an open statement. center>x>4 is not the logical negative of x<4

where the common universe is {1,2,3,4,5,6,7}. This is because both open statements assign the same truth value (F) to 4. Logical negatives must assign opposite truth values to every object in the universe.

A simpler example of incompatibility are the open statements: x = 3,    x = 6 where the common universe is {1,2,3,4,5,6,7}. It is obvious that both cannot be true, but both can be false. The following table supports this statement:

                          replace x by      x = 3    x = 6
                               1                    F          F
                               2                    F          F
                               3                    T          F
                               4                    F          F
                               5                    F          F
                               6                    F          T
                               7                    F          F

This table suggests the following definition:

[3.3] Incompatible open statements Two open statements with the same universe are incompatible if and only if each object in the universe is assigned an F from one or both of them. (No object receives T's from both of the open statements.)

Intuitively speaking, incompatible open statements present conditions that are too severe for anything to satisfy all of them. There is an obvious extension of incompatibility to more than two open statements. Any open statement and its negative are incompatible, because both cannot become true for any object in its universe. Incompatibility is more general than negativism (denial).

In algebra incompatible equations are called inconsistent. The equations

x + 1 = 4   and   x + 21 = 88
are inconsistent, where the universe is the collection of all integers. The important thing here is that no number can satisfy both equations. It is only a minor observation that many numbers satisfy neither equation.

Again the reader should be reminded that open statements themselves do not have any truth values. But they have component statements that have truth values, and which assign truth values to objects in the universe of the open statement. But a [pair of open statements with the same universe inherit logical equivalence, denials and incompatibility directly from the truth values of their components and from the pairs of truth values assigned to each object in their universes.

Further discussions of open statements will be found in the next volume. Diagrams there can make more undestandable open statements. the meanings of those open statements.