Return to main text in Chapter 2
Additional Material for Chapter 2
Intuitive introduction to open statements
Here is a simple example of truth values being assigned to (the names of) objects. A coach picks 12 persons from a group of 20 people to be on his team. He does this by marking a list of all 20 names. He puts a T by the name of anyone selected, and an F by the name of anyone not selected. On the list there will be twelve names with T's and eight names with F's.
Consider now a numbered list of three logical statements:
1. All triangles have four sides
2. The USA is in North America
3. The moon is larger than the earth.
The numbers 1,2,3 serve as names of these statements. The statements have truth values and "give" these truth values to the numbers
1 receives an F
2 receives a T
3 receives an F
In both examples a list is used to assign truth values to names of objects. In these discussions an open statement is a much more common method of doing this assignment. One form of an open statement is an algebraic equation with an unknown in it. Consider the equation x + 67 = 69. It is easy to find the solution by subtracting 67 from both sides of the equation. Instead, try the first three natural numbers 1,2,3.
Try 1 (replace x by 1): 1 + 67 = 69. This results in the false statement that 68 = 69.
Try 2 (replace x by 2): 2 + 67 = 69. This results in a true statement that 69 = 69.
Try 3 (replace x by 3): 3 + 67 = 69. This results in a false statement 70 = 69.
The equation x + 67 = 69 has assigned truth values to the numbers 1,2,3: 1 F, 2 T, 3 F. (The solution is that number that receives a T.)
Equations with an unknown are one form of an open statement. There is a generalization that allows words and an unknown to form an open statement.
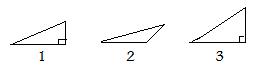 Consider now three triangles as shown. They are identified by numbers 1,2,3. Instead of an equation, consider the statement "x is a right triangle". Replacing the x by each of the numbers 1,2,3 generates a list of components
Consider now three triangles as shown. They are identified by numbers 1,2,3. Instead of an equation, consider the statement "x is a right triangle". Replacing the x by each of the numbers 1,2,3 generates a list of components
1 is a right triangle
2 is a right triangle
3 is a right triangle
These statements also assign truth values to the three numbers: 1 T, 2 F, 3 T. Only triangle 2 is not a right triangle.
It is important to notice where the objects are located. They are in some collection which is called the universe. Anything outside the universe is ignored. In the examples the universe was the collection of the first three natural numbers, 1,2,3. Usually the universe changes for different discussions.
Direct proof
For a direct proof that an open statement q(x) is universally true, it must be shown that every object in the universe receives a T (but if the universe is empty then q(x) is automatically universally true). If there are only a few objects in the universe, say a,b,c,d,e, ... then they may be tested individually, more exactly, each of the components q(a), q(b), q(c), q(d), q(e), ... can be determined to be true. For example, if q(x): x < 9, and the universe is {1,2,3,4,5} it is easily verified that all the components
1 < 9, 2 < 9, 3 < 9, 4 < 9, 5 < 9
are true. There are no counterexamples.
Often there are too many objects in the universe for individual examination. It is difficult if not impossible to check individually every component of q(x) for its truth value, or, equivalently, what truth value each object in the universe receives from q(x). For example,
let q(x): x2 + 3x + 2 = (x + 1)(x + 2) with universe {1,2,3,..., 999999,1000000}
A million verifications that q(x) assigns a T to each number is not practical. Instead, the laws of elementary algebra allow a multiplication to confirm the equality:
(x + 1)(x + 2) = x(x + 2) + 1(x + 2) = xx + 2x + 1x + 2 = x2 + 3x + 2
A similar idea exists in logic. In the discussion of logical statements (before open statements), it was proven that if
expression = p and (p ==>q)
then the implication
expression implies q
is a tautology (always true). A truth table shows that it is impossible for expression to be true and q to be false for any truth values of p,q. In practical use the implication p ==> q is actually proven through a telescoping of implications:
p ==> r1, r1 ==> r2,
r2 ==> r3, ..., rn ==> q
 Consider now three triangles as shown. They are identified by numbers 1,2,3. Instead of an equation, consider the statement "x is a right triangle". Replacing the x by each of the numbers 1,2,3 generates a list of components
Consider now three triangles as shown. They are identified by numbers 1,2,3. Instead of an equation, consider the statement "x is a right triangle". Replacing the x by each of the numbers 1,2,3 generates a list of components