Additional Material for this Chapter
Exercises for this Chapter
Answers to Exercises
Return to index of all chapters in this volume
Volume A Chapter 2
Sets and Open Statements
Section 1: Introduction
In these volumes the word object will have an extended meaning. It could be something physical, such as a person, a grain of sand, a small round ball, a building, ... . But it may also be something abstract, like a number 5 or a geometric point. Whatever it is, it is usually indivisible (exceptions in Section 5). Objects may be collected together: physically such as balls in a bag or abstractly, such as points on some straight line. All such collections will be called sets. (In advanced mathematics there are discussions about some not very "nice" collections which produce logical paradoxes, e.g. the Russel paradox. In these volumes there will be no such weird collections of objects!)
Although no rigorous definition of a set is attempted here, some simple conditions may be imposed:
[1.1] (Definitive conditions for sets)
(a) An object is either in a set or not in a set.
(b) Two sets are equal if and only if they contain exactly the same objects.
The phrase "an object is a member of a set" is equivalent in meaning to the phrase "an object is in a set." The phrase "an element in a set" is used in some other textbooks.
The notation b ∈ S means that object b is in set S. However, in these volumes the English phrase will be used.
In Volume B (Numerical systems) are discussions about objects called natural numbers and their properties. They are the familiar numbers without end for counting:
1, 2, 3, 4, 5, 6, ......100, ...., 10000000,..... 19278498694373, .... →
They are whole numbers, no decimals, no fractions, no negatives, no largest (always one bigger), and in these discussions, no zero.
Collections of these objects can be made. For example, the sets of the first two, five and nine natural numbers are:
N2 = {1,2}, N5 = {1,2,3,4,5}, N9 = {1,2,3,4,5,6,7,8,9}
These three sets show two things:
(a) Some sets may be declared by listing all its objects in between symbols { }. To fulfil condition [1.1a] any object not in the listing is not in the set.
(b) Sets may have names. In this case they are N2, N5, N9.
The objects 3, 5, 6 are in N9. The objects 10, 11 are not members of N9.
The reader can easily determine what objects are in the sets
N6, N100, Nn where n=7.
In these discussions the name of the infinite set of all natural numbers is N,
N = {1,2,3,4,5,6,...............→}.
It is not always necessary to give names to sets. For example the set of all prime numbers in N9is {2,3,5,7}.
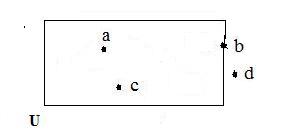 Usually all objects involved in a discussion form a collection called a universe. Objects outside a universe are ignored and cannot be involved. An interior of a rectangle may serve as an example of a universe. Let its name be U. In the adjacent figure a,b,c,d are names of points. Points a,c are in U, and points b,d is not in U.
Usually all objects involved in a discussion form a collection called a universe. Objects outside a universe are ignored and cannot be involved. An interior of a rectangle may serve as an example of a universe. Let its name be U. In the adjacent figure a,b,c,d are names of points. Points a,c are in U, and points b,d is not in U.
However, there may be more than one universe, often because some objects are very different from some other objects in the discussion. For example, a single discussion involves a universe of numbers and a universe of points. The discussion may relate the numbers to the points, as is done with the numberline.
It is necessary to distinguish objects from the sets that objects are in. The object 1 is not the same as the set
N1 = {1}
consisting of the single number 1.
***
Objects are inside universes. It is useful to consider a set inside a universe.
[1.2] A set inside a universe is a collection of objects that belong to that universe. It is also called a subset of that universe.
In discussions below the letter S, sometimes with a numerical subscript, is used often as a name for some subsets.
(Numerical) Example 1: The set {2,5,6,8} is a subset of the universe N9. But the set {5,7,100} is not a subset of N9 because 100 is not in the universe.
The collection of objects in a subset may be made by selecting objects satisfying some rule, from all the objects in the universe. (But nothing is removed from the universe while collecting the objects.)
(Numerical) Example 2: In the universe N9 collect all the numbers between 3 and 8. Equivalently, this collection is the set {4,5,6,7} which is a subset of the universe N9.
 (Geometric) Example 3: In the adjacent figure the universe consists of all points inside and on the rectangle. The interior of the circle together with the circle itself is a subset of the universe. If c is the center then the subset consists of all the points whose distance from c is < the radius of the circle.
(Geometric) Example 3: In the adjacent figure the universe consists of all points inside and on the rectangle. The interior of the circle together with the circle itself is a subset of the universe. If c is the center then the subset consists of all the points whose distance from c is < the radius of the circle.
For any universe U, two extremes of selection are allowed:
(a) All objects in U are selected Therefore, every universe is a subset of itself.
(b) No objects in U are selected. Then the subset is empty. It is given the permanent name ∅. Later, it will be shown that logic demands this same empty set ∅ to be a subset of every universe.. (Also more "weird" facts of this set will be revealed.)
***
Consider the following statements:
Table 1 (Components):
1 is between 3 and 8
2 is between 3 and 8
3 is between 3 and 8
4 is between 3 and 8
5 is between 3 and 8
6 is between 3 and 8
7 is between 3 and 8
8 is between 3 and 8
9 is between 3 and 8
All the statements are similar. Any of the nine statements can be reproduced by replacing the x in the single open statement
(*) x is between 3 and 8
by the (name of) any object in the universe N9. The nine statements are called components of the open statement (*).
Needed is a notation, called function notation, that is a name for the open statement displaying the variable:
p(x): x is between 3 and 8
x can be replaced by another vatriable, say y or z:
p(y): y is between 3 and 8
p(z): z is between 3 and 8
and also by (names of) objects in the universe N9. But these substitutions produce the components:
p(1): 1 is between 3 and 8
p(2): 2 is between 3 and 8
......
p(9): 9 is between 3 and 8
Therefore, the nine components of p(x) are p(1), p(2), ..., p(9).
 Referring to the adjacent figure, let q(y) the open statement
Referring to the adjacent figure, let q(y) the open statement
q(y): point y is inside the circle
It is impossible to list all of the components of q(y) because there are infinitely many points in the universe (inside the rectangle). But four components can be displayed because four points have names a,b,c,d:
q(a): point a is inside the circle
q(b): point b is inside the circle
q(c): point c is inside the circle
q(d): point d is inside the circle
[1.3] (Open statements and components) An open statement in a variable with universe is a form in which if the variable is replaced by (the name of) any object in the universe, then the open statement becomes a logical statement, called a component of the open statement.
Notation: if p(x) is an open statement in x with universe U and b,c,d are (names of) objects in U, then p(b), p(c), p(d),... are logical statements derived from p(x) by replacing x by b, or x by c, or x by d.
p(x) is called the function notation for an open statement.
It is important to realize that open statements do not have truth values. But their components, produced by replacing the variable x, y, or z by (names of) specific objects in the universe, are logical statements and therefore must have truth values. Such a componemt is true (T) or false (F). Table 2 displayes the open statement, its components and truth values of the components
Table 2:
p(x): x is between 3 and 8. p(x) has no truth value
p(1): 1 is between 3 and 8. p(1) is F
p(2): 2 is between 3 and 8. p(2) is F
p(3): 3 is between 3 and 8. p(3) is F
p(4): 4 is between 3 and 8. p(4) is T
p(5): 5 is between 3 and 8. p(5) is T
p(6): 6 is between 3 and 8. p(6) is T
p(7): 7 is between 3 and 8. p(7) is T
p(8): 8 is between 3 and 8. p(8) is F
p(9): 9 is between 3 and 8. p(9) is F
Taken from the last column of the above table, Table 3 shows the truth values assigned directly to the objects:
Table 3:
1 F 2 F 3 F 4 T 5 T 6 T 7 T 8 F 9 F
[1.4] (Open statements giving truth values to objects) A open statement with a universe assigns a truth value to each object in that universe by copying the truth value of the component containing that object.
The open statement
q(x): x + 1 is between 4 and 9
with universe N9 also produces Table 3. Logic is interested only in the objects and truth values assigned to them, not in the method of assignment. This leads to the idea of logical equivalence.
There are different methods for asigning truth values to every object in some universe. One method is by selection. If an object is selected, assign a T to it. If rejected, assign an F. Different open statements also assign truth values to every object. Two methods for assigning truth values to all objects in a universe are logically equivalent if and only if they together assign two equal truth values to each object. In particular, this applies to open statements.
[1.4a] (Equivalent open statements) Two open statements are logically equivalent if and only if they have the same universe and the truth values they assign to any object are the same.
Notation: p,q are equivalent if and only if truth values p(x)=q(x) for each object in the common universe.
In the assignment of truth values to all objects in a universe it may happen that the same truth value is assigned to every object. If the truth value is T, then the event is important enough to be recognized in the following way:
[1.5] (Universally true open statements) An open statement is universally true if and only if all of its components are true (it assigns a T to every object in the universe)
Notation: for all x in U p(x) is true. (Note: the phrase "is true" is usually omitted).
The phrase "for all x in U" is called a positive universal quantifier.
Another notation for the positive universal quantifier is ∀x in U. But in most discussions in these volumes, the English words will be used.
Example: The open statement
x < 10 with universe is N9
is universally true because all components
1<10, 2<10, 3<10, 4<10, 5<10, 6<10, 7<10, 8<10, 9<10
are true. And each object in the universe N9 is assigned a T by the open statement x < 10:
1 T, 2 T, 3 T, 4 T, 5 T, 6 T, 7 T, 8 T, 9 T
The notations for all this are
for all x in N9, x<10
and
∀x in N9, x<10
If the objects in the universe are examined for attached truth values, and no object is assigned an F, then it can safely be assumed that the open statement is universally true. An open statement is universally true if and only if it has no false components (no object in the universe is assigned an F). But if an open statement is not universally true some object has been assigned an F. But if an object is assigned an F and that object has a special name. Acounterexample to an assertion that an open statement is universally true is any object in the universe that has been assigned an F by the open statement.
In Table 3 above, object 2 was assigned an F. Then 2 is a counterexample to the statement
for all x in N9, x is between 3 and 8.
Therefore the open statement x is between 3 and 8 is not universally true.
The following implies definition [1.5] and is sometimes useful to prove open statements are universally true.
[1.6] (Universally true open statements) An assertion that an open statement with a universe is universally true is itself true if and only if there exists no counterexample in that universe.
There may be more than one counterexample, but only one is needed to disprove the universality of truth.
However there are open statements that go to the extreme and assign an F to every object in the universe. For example, the open statement
x2 = 5
with universe N9 is universally false. No natural number can satisfy this equation.
One way way of saying that an open statement p(x) is universally false is
for no x in U, p(x) is true
But this invents a negative universal quantifier "for no x in U". To avoid more universal quantifiers, the above phrase can be stated an equivalent way:
for all x in U, ~p(x)
This is closer to saying literally that all components of p(x) are false.
This equivalence means no need to use negative universal quantifiers. The open statements may be negated (denials) instead and positive universal quantifiers may be used. Hereafter the "positive" may be omitted from the expression "positive universal quantifier."
However, universally false open statements are seldom discussed. Most assignments by open statements involve at least one T, perhaps more.
[1.7] (Existentially true open statements) An open statement with a universe is existentially true if and only if it has at least one true component (it assigns at T to at least one object in the universe).
Notation1: p(x) is existentially true if and only if for some object b in the universe, p(b) is true.
Notation2: there exists an x in U, p(x) is true [usually the phrase "is true" is omitted]
Examples: with universe N9, both the open statements x < 10 and x is between 3 and 8 assign T to at least one object 5. (Actually they assign T to 4,5,6,7.) Both open statements are existentially true. However, x2 = 5 is universally false and cannot be existentially true.
The notations
The existential quantifier does not specify how many objects are assigned T, only tha there is at least one object. Sometimes it is desirable that there is exactly one object, and no more, that is assigned a T.
[1.8] (Uniquely existentially true open statements) An open statement with a universe is uniquely existentially true if and only it has exactly one true component (exactly one object that is assigned a T, all others are assigned F).
Notation1: there exists exactly one x in U such that p(x) is true
Notation2: there exists a unique x in U, p(x)
Example1: For the open statement
x is between 5 and 7
with universe N9, the quantified expression
there exists a unique x, x is between 5 and 7
is true.
Example2: The solutions to linear equations such as 3x = 12 are unique.
Example3: The ratio of the circumference of any circle to the length of its diameter is unique, namely π
In many textbooks the uniquely existential quantifier "there exists a unique x in U" is expressed by the symbolic phrase
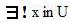 .
For typographical reasons this notation will not be used anywhere.
.
For typographical reasons this notation will not be used anywhere.
Let the reader compare the following equivalence with [1.6]: for all x in U, p(x) if and only if ~ there exists an x in U, ~p(x).
-----
[1.9a] (Equivalent open statements) Open statements with the same universe are logically equivalent if and only if they together assign equal truth values to each object in the universe.
Notation: p(x) <==> q(x) if and only if each object is assigned TT or FF.
The word "logically" often will be omitted.
There are different methods of assigning truth values to all objects in some universe U. The assignment of truth values in U can be done by selection. If an object is selected, assign a T to it. If rejected, assign an F. An open statement with universe U is also a method for assigning truth values. Sometimes the two methods are equivalent.
The following is a negative way of defining equivalent open statements,. Yet it is equivalent to [1.9a].
[1.9b] (Equivalent open statements) Open statements with the same universe are logically equivalent if and only if they never assign different truth values to any object in the universe.
Notation: p(x), q(x) are equivalent if and only if no object is assigned TF nor FT.
By [1.9b] two universally true open statements with the same universe must be equivalent. The same is a fact for two universally false open statements with the same universe.
If all the objects in a universe have been assigned truth values, then all those objects assigned a T form a distinguished set, called truth set. When open statements are algebraic expressions, the truth sets are often called the solution sets. For example, the solution set of
3 < x < 8
is {4,5,6,7}.
The following "set builder notation" denotes the truth set of an open statement p(x) with universe U:
{x in U | p(x)}
Intuitively speaking, it goes through all the objects in the universe and collects all those with a T into a set. More exactly, it is the set of all objects in U that are assigned T by the open statement p(x).
For example, {x in N9 | 3 < x < 8} = the set of all objects in N9 that are between 3 and 8 = {4,5,6,7}.
The idea of truth sets reveals an intimite connection between sets and open statements. According to [1.4] every open statement has a (unique) truth set. Conversely for any set S in the universe there is an open statement x is in S whose truth set is S. It is called the trivial open statement for S. There are other open statements with that same universe and with that same truth set.
[1.10] (Relationship between sets and open statements)
(a) Every open statement determines a subset of its universe, namely its truth set.
(b) For every subset of a universe there is an open statement whose truth set equals that subset, namely the trivial open statement.
Often in the same discussion there are more than one open statement all with the same universe. Each independently assigns truth values to all the objects in that universe. If there are two open statements then each object receives two truth values.
For any set S in a universe U there are many open sets p(x), q(x), r(x), ... whose truth sets equal S. For example:
x > 3 and x < 8, x + 1 is between 4 and 9, x is between the roots of x2 - 11x + 24, x is in {4,5,6,7}
where S = {4,5,6,7}. However, all such open statements must be equivalent to each other, and therefore, equivalent to the trivial open statement x is in S.
[1.11] (Equivalent open statements) Open statements with the same universe are equivalent if and only if they all have the same truth set.
The argument supporting [1.11] is simple.
If the open statements are equivalent, then each object in the universe receives equal truth values from the open statements. Therefore, the objects receiving a T from one open statement must also receive a T from all the other open statements. So their truth sets must be the same.
Conversely, suppose the open statements have the same truth set. Then all open statements assign a T to every object in the truth set and an F to every object not in the truth set. Therefore, equal truth values assigned to all objects in the universe. By [1.9] the open statements are equivalent.
Examples:
The equations x + 1 = 5 and x + 2 = 6 with universe N are equivalent because they have the solution set {4}.
If both sides of an equation are multiplied by the same natural number then an equivalent equation is obtained.
-----
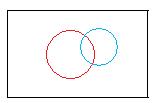 In the following sections there are discussions involving more than one open statement, all with the same universe. Two open statements will assign two truth values to each object and determine two subsets (truth sets) in that universe, three open statements - three truth values to each object and three subsets (truth seets) in that universe, etc. The assignments of truth values to objects are done independently. Sometimes colors will be used to coordinate names, open sets and geometric models. The adjacent figure is the geometric model of the truth sets S1, S2 of two unspecified open statements p(x), q(x) . Depending on the positions of the circles, these open statements may assign any of the following pairs of truth values to each object in the universe:
In the following sections there are discussions involving more than one open statement, all with the same universe. Two open statements will assign two truth values to each object and determine two subsets (truth sets) in that universe, three open statements - three truth values to each object and three subsets (truth seets) in that universe, etc. The assignments of truth values to objects are done independently. Sometimes colors will be used to coordinate names, open sets and geometric models. The adjacent figure is the geometric model of the truth sets S1, S2 of two unspecified open statements p(x), q(x) . Depending on the positions of the circles, these open statements may assign any of the following pairs of truth values to each object in the universe:
(#)
TT,
TF,
FT,
FF
Here is a numerical example of two specific open statements:
Let the universe be N9, and p(x),
q(x) be open statements with that universe, and defined by
p(x): 3 < x, q(x): x < 8
Then from the pairs
p(1)q(1),
p(2)q(2),
p(3)q(3),
p(4)q(4),
p(5)q(5),
p(6)q(6),
p(7)q(7),
p(8)q(8),
p(9)q(9)
each object in the universe receives two truth values:
1 FT
2 FT
3 FT
4 TT
5 TT
6 TT
7 TT
8 TF
9 TF
Notice that no object in this example receives the pair FF. Intuitively speaking, if either open statement assigns an F, the other open statement cannot assign an F to that same object. As will be seen later, such a restriction means that some relation exists between the open statements, and also between their truth sets. The following concerns open sets without any restrictions on the assignments of truth values to objects.
[1.12] (Logically unrelated open sets) Two open statements with the same universe are unrelated if together their assignments of truth values to all the objects in the universe involves all four pairs of truth values shown in (#) above.
Notation:
In the universe, unrelated open sets p(x), q(x)
assign TT to some object,
assign TF to another object,
assign FT to another object,
assign FF to another object.
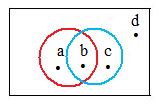 The adjacent figure shows the truth sets of two unrelated open sets. The trivial open statements involving point x
The adjacent figure shows the truth sets of two unrelated open sets. The trivial open statements involving point x
x is inside the red circle,
x is inside the blue circle
assign the following pairs of truth values to the four points a, b, c, d:
b TT
a TF
c FT
d FF
The pairs of truth values assigned to these four points are enough to show that the open statements are unrelated.
The definition [1.9b] confirms that the truth sets of equal open statements are not unrelated.
 Usually all objects involved in a discussion form a collection called a universe. Objects outside a universe are ignored and cannot be involved. An interior of a rectangle may serve as an example of a universe. Let its name be U. In the adjacent figure a,b,c,d are names of points. Points a,c are in U, and points b,d is not in U.
Usually all objects involved in a discussion form a collection called a universe. Objects outside a universe are ignored and cannot be involved. An interior of a rectangle may serve as an example of a universe. Let its name be U. In the adjacent figure a,b,c,d are names of points. Points a,c are in U, and points b,d is not in U. (Geometric) Example 3: In the adjacent figure the universe consists of all points inside and on the rectangle. The interior of the circle together with the circle itself is a subset of the universe. If c is the center then the subset consists of all the points whose distance from c is < the radius of the circle.
(Geometric) Example 3: In the adjacent figure the universe consists of all points inside and on the rectangle. The interior of the circle together with the circle itself is a subset of the universe. If c is the center then the subset consists of all the points whose distance from c is < the radius of the circle.
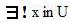 .
For typographical reasons this notation will not be used anywhere.
.
For typographical reasons this notation will not be used anywhere.
 In the following sections there are discussions involving more than one open statement, all with the same universe. Two open statements will assign two truth values to each object and determine two subsets (truth sets) in that universe, three open statements - three truth values to each object and three subsets (truth seets) in that universe, etc. The assignments of truth values to objects are done independently. Sometimes colors will be used to coordinate names, open sets and geometric models. The adjacent figure is the geometric model of the truth sets S1, S2 of two unspecified open statements p(x), q(x) . Depending on the positions of the circles, these open statements may assign any of the following pairs of truth values to each object in the universe:
In the following sections there are discussions involving more than one open statement, all with the same universe. Two open statements will assign two truth values to each object and determine two subsets (truth sets) in that universe, three open statements - three truth values to each object and three subsets (truth seets) in that universe, etc. The assignments of truth values to objects are done independently. Sometimes colors will be used to coordinate names, open sets and geometric models. The adjacent figure is the geometric model of the truth sets S1, S2 of two unspecified open statements p(x), q(x) . Depending on the positions of the circles, these open statements may assign any of the following pairs of truth values to each object in the universe:
 The adjacent figure shows the truth sets of two unrelated open sets. The trivial open statements involving point x
The adjacent figure shows the truth sets of two unrelated open sets. The trivial open statements involving point x