Additional Material for this Chapter
Exercises for this Chapter
Answers to Exercises
Return to index of all chapters in this volume
Volume A Chapter 1
Logical Thinking
In order to communicate general thoughts, a person uses a language and and from it organizes words according to some meaningful and grammatical way. Similarly, to communicate thoughts about mathematics, a person organizes words and symbols according to a meaniful and logical way. Intuitively speaking, logic is a language for mathematics. The use of logic appears in discussions supporting or proving theorems. Although discussions in these volumes follow the principals of logical reasoning, they usually mix in those discussions very intuitive yet pertinent remarks to make the discussions more understandable. Simple and clear examples and diagrams often accompany definitions and theorems also to promote understanding.
Section 1 Logical Statements and Their Equivalence
A statement is sometimes said to be a complete thought. It becomes a basic unit in all discussions of logic when it is fact or falsehood.
[1.1] (Logical statement) A logical statement (or proposition) is a statement that is true or is false (but not both).
By their meanings some statements are obviously true, other statements are obviously false. True are the statements:
2+3=5, all triangles have three sides, Los Angeles is a city in the state of California (USA)
False are the statements:
4+2=7, A right angle is equal to 120°, the earth is smaller than its moon
The following pairs of statements have opposite truth values:
2+3 = 5, Mexico is in Europe
line1 is parallel to line2, line1 intersects line2
The "true" and "false" (often abbreviated T and F) assigned to the different logical statements given above are called truth values. By definition [1.1] every logical statement must have a truth value. But consider the statement:
There is life on some planet outside our solar system
It may be true or it may be false. Its truth value is unknown, but it does have a truth value. A conjecture is a logical statement with an unknown truth value, but has the possibility of being true. Later a conjecture may turn out to be true or turn out to be false. Questions and incomplete statements cannot be logical. "Do you like the color red?" is not a logical statement.
Every logical statement must have a truth value, or it is not a logical statement..
To evaluate logically a statement means to assign a truth value to that statement. In these discussions the evaluation of a statement in English usually is obvious from its meaning and common knowledge.
Statements in these discussions are phrased in Englich or symbols of mathematics and logic. Often they can be given using different words or symbols, but somehow give the same meanings. Logic, however, is interested only in the truth values of logical statements. A pair of such statements may concern very different topics, but their truth values are what is important.
[1.2] (Equivalent statements) Logical statements are (logically) equivalent if they have the same truth value.
The two logical statements 2+3=5 and "all triangles have 3 sides" are logically equivalent because both are true.
Also 4+4=9 and "all houses are red" are logically equivalent. This time they are both false.
But the statements 5+4=9 and "All squares have 5 sides" have opposite truth values, and therefore are not logically equivalent.
The three statements
2 + 3 = 5, 2 + 3 = 5 is true, it is true that 2 + 3 = 5
are equivalent: all three are true.
And the three statements
all triangles have 4 sides, all triangles have 4 sides is true, it is true that all triangles have 4 sides
are also equivalent: all are false.
Inclusion of the phrase is true or it is true that does not change meanings nor truth values. Therefore, the phrases are not necessary. But they may be included sometimes to make a discussion more understandable. However, the phrases is false and it is false that change truth values and cannot be omitted.
In algebra the letters x,y,z,... are used often to represent unknown or known numbers. They receive values when assigned numbers. x=3 gives x a value. In another problem x might be given another value, say 5. In a similar way, a logical variable, p,q, or r might be assigned a logical statement. A logical statement is a value given to a logical variable. For example,
p: the moon is smaller than the earth q: every triangle has 5 sides
assigns a true statement to p and a false statement to q. In a sense, then p receives a T and q receives an F.
A logical variable is a symbol which can be assigned a logical statement. Any assignment gives the variable a truth value. In these discussions, if a logical statement is assigned to a logical variable then a colon (:) is placed between the variable and its logical statement.
In algebra, an equal sign is placed between a variable and a value assigned to it: x = 2, y = -5, z = 16.4. But the assignment of 2 to x is not permanent. In another problem x may be assigned a different value. It is convenient to use the same variables repeatedly in different discussions if no confusion results. Similarly, the same logical variable may be re-used and assigned different statements. The variable p may be associated with a statement in a discussion, but p may be associated with another statement in a different discussion. In discussions here there are no logical symbol that has a permanent truth value, the same in all discussions.
If a logical variable is assigned a logical statement, it is convenient to pass the truth value of the statement onto the variable. But if a variable is not assigned a statement, it is often convenient to think of the variable as having unknown truth value. It could be either T or F.
The statement Japan is larger than Russia is obviously false. It receives a truth value F. The statement Japan is not larger than Russia is true. It is a denial or negative of the first statement.
The statement 3 + 2 is not equal to 5 is false. The removal of "not" converts it to 3 + 2 = 5 which is true. The second statement is a denial of the first. These denials were obtained by grammatical methods. They are called semantic denials in these discussions.
Consider the following two statements:
Japan is larger than Russia,
Japan is not larger than Russia
From their meanings, the second statement with the added word "not" is a denial of the first. More important, the two statements have opposite truth values. Concerning the following two statements:
3 + 2 is not equal to 5 3 + 2 = 5
The second statement is a denial of the first. The word "not" has been removed. Another method for forming denials without internal grammatical changes in a statement is seen in the following:
Japan is larger than Russia,
it is false that Japan is larger than Russia
3 + 2 is not equal to 5
it is false that 3 + 2 is not equal to 5
In general, if p is any logical statement, then it is false that p is the denial of p. The Spanish tilda (~) replaces the phrase "it is false that" to get the notation ~p do denote the denial of p. Intuitively speaking, applying the tilda to a logical statement is like applying the negative sign to a number.
If p: 4 + 5 = 9, then ~p: it is false that 4 + 5 = 9. This shows that the denial of a true statement is a false statement.
[1.3] (Logical negation) Any logical statement with the truth value opposite to the truth value of a given logical statement is (also) a (logical) denial or a (logical) negative of that given logical statement.
Notation: q is a logical denial of p if and only if p and q have opposite truth values.
Intuitively speaking, logic cannot distinguish between q and ~p. This fact allows a very disimilar statement to be a denial: q: 2 + 4 = 10 is denial of p: all triangles have 3 sides. (Perhaps it may be better to think of it as a logical negative.) Fortunately, such strange situations do not play a major role in discussions here.
A free logical variable p has no attached logical statement to give it a truth value. Of all the statements that can be attached there are only two truth values possible for p. This fact can be expressed as follows:
[1.4] (Table of possibilities for a single variable) A table of possibilities for 1 logical variable p
p
T
F
Actually [1.4] is a repeat of definition [1.1] using logical symbols. The following tables are read by rows (not by columns).
[1.5] (Table of possibilities for two variables) A table of possibilities for 2 logical variables p,q
p q
T T
T F
F T
F F
[1.6] (Table of possibilities for three variables) A table of possibilities for 3 logical variables p,q,r
p q r
T T T
T T F
T F T
T F F
F T T
F T F
F F T
F F F
There are larger tables of possibilities for 4,5,... variables, but seldom will discussions involve more than 3.
Any logical statement and its denial have opposite truth values. This is expressed in the following table.
[1.7] (Truth table for logical denial) A truth table for a logical statement p and its denial:
p ~p
T F
F T
This table is an expansion of [1.4].
Consider the expression p has the same truth value as q. Another way of saying it is p,q are logically equivalent The symbol ←→ is used to declare equivalence Using [1.2] the following table can be formed:
[1.8] (A truth table for equivalence) A truth table for p,q are equivalent
p q p ←→ q
T T T (p,q have the same truth value, so it is true that they are equivalent)
T F F (p,q have opposite truth values; it is false that they are equivalent)
F T F (p,q have opposite truth values; it is false that they are equivalent)
F F T (p,q have the same truth value, so it is true that they are equivalent)
The first line of a truth table (in boldface) is called the header. In the header is a horizontal list of variables and a logical expression to be evaluated. On the next horizontal lines are different possibilities for the truth values of the variables. (A table of possibilities is always a part of any truth table.) Each possibility determines a truth value for the expression. In [1.7] the definition [1.2] of equivalence does the determination. The truth value is always written under the expression.
Three notations are used in these discussions to declare the equivalence of p,q:
p is equivalent to q;
p ↔ q;
p if and only if q.
(In some places another form of equivalence is used:
A necessary and sufficient for q is that p.
More of this form will be discussed later.)
Any of these three notations suggest that two logical statements can be combined by placing some connective between them. As a result a logical compound statement is produced. Any logical statement and any logical compound statement will be called a logical expression. For example, p ←→ q is a logical compound statement and also a logical expression. In these discussions the logical statements p, q are said to participate in the expression. The variables p,q,r by themselves also are considered logical expressions.
More logical connectives will be introduced and discussed in the following sections.
More variables may be in the header of a truth table. In general,
[1.9] (Table of possibilities for n variables) For n logical variables there are 2n possibilities.
Instead of T and F the numbers 1 and 0 could be used in the tables. (These conform to probability values of complete success and utter failure.) Replacing T,F in the table [1.4] by 1,0 produces the following table:
[1.10] (0,1 truth table equivalence) A truth table for p,q are equivalent
p q p ↔ q
0 0 1
0 1 0
1 0 0
1 1 1
In these discussions the T-F notation is used most of the time. Yet some interesting applications will be expressed in the 1-0 notation. In some places (as in [1.8]) the tables of possibilities in the 0-1 notation are written in the reverse order of the T-F notation. The idea here is that 00, 01, 10, 11 are numbers of increasing size.
Section 2 Logical conjunction and logical alternation
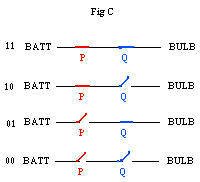 An electrical switch either allows electricity to pass through (it is on, it is closed) or it prevents electricity from passing through (it is off, it is open). The adjoining figure Fig C shows four diagrams of a battery BATT and a light bulb BULB connected by a wire that has two switches P and Q (in series). Depending upon the conditions of the switches electricity can flow between the BATT and the BULB and make the BULB shine light. For this to happen both switches must be closed (Fig C11 at the top). Otherwise, if either switch is open (Fig C10, Fig C01 in the middle), or if both are open (Fig C00 at the bottom), then electricity cannot go between BATT and BULB.
An electrical switch either allows electricity to pass through (it is on, it is closed) or it prevents electricity from passing through (it is off, it is open). The adjoining figure Fig C shows four diagrams of a battery BATT and a light bulb BULB connected by a wire that has two switches P and Q (in series). Depending upon the conditions of the switches electricity can flow between the BATT and the BULB and make the BULB shine light. For this to happen both switches must be closed (Fig C11 at the top). Otherwise, if either switch is open (Fig C10, Fig C01 in the middle), or if both are open (Fig C00 at the bottom), then electricity cannot go between BATT and BULB.
The possible truth values for the statements
p: electricity can flow through switch P,
q: electricity can flow through switch Q:
are pT qT, pT qF, pF qT, pF qF.
Each possibility has an effect on the truth value of the statement statement:
electricity can flow between BATT and BULB.
It may be true or false. Therefore, they are logical statements. The last statement about flowing through both switches is equivalent to saying
p and q
This says that switch P is closed and switch Q is closed, which may or may not be true. This physical model involving switches suggests the following definition in English and in logic:
[2.1] (Conjunction) A conjunction is formed when the word "and" is placed between two logical statements. The conjunction is true if and only if both logical statements are true.
Notation: The conjunction p and q is true if and only if both p and q are true.
Another notation for conjunction is ∧: p ∧ q. In these volumes the English word will be used. Sometimes the symbol will be used to avoid confusion.
The logical statements p, q participate in the conjunction p and q. They will be called (logical) participants
The conjunction itself becomes a logical statement because definition [2.1] gives it a truth value.
If either p is false or q is false (or both are false) then p and q is false.
[2.2] (Truth table for conjunction) A the truth table for logical conjunction of statements p,q
p q p and q
T T T
T F F
F T F
F F F (because of the last F here, conjunction is different from equivalence)
The form q and p is another way a conjunction can be formed. Using the word-definition of conjunction, instead of the notation, following truth table for q and p can be constructed.
A the truth table for logical conjunction of statements q,p
p q q and p
T T T
T F F
F T F
F F F
The columns under q and p and p and q are identical, signifying equivalence.
[2.3] (Conjunction is commutative) The truth value of a conjunction is not changed if the logical participating statements are switched.
[2.4] Extended logical conjunction Logical conjunction can be extended to include more than two statements by placing the word "and" between the statements. The extended conjunction is true if and only if all the logical statements in it are true
Notation: p and q and r and ... is true if and only if all statements p,q,r,... are true.
p and q and r and ... is false if any one (or more) of p,q,r,... is false.
The truth table for a conjunction of three variables has under the expression a single T and seven F's. (See [1.5] above.)
It is interesting to see what happens if the 1-0 notation is used in place of T-F (1 replaces T, 0 replaces F.). The truth table [2.2]becomes:
p q p⋅q
1 1 1
1 0 0
0 1 0
0 0 0
Now rearrange the table of possibilities into numerical order:
p q p⋅q
0 0 0
0 1 0
1 0 0
1 1 1
But this is the multiplication table for multiplying the numbers 0 and 1. In fact many years ago logical conjunction was written as an algebraic product of two variables.
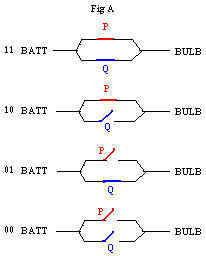 The adjoining figure Fig A shows four diagrams of a battery BATT and a light bulb BULB connected by a wire that has two branches (in parallel). In each branch is a switch, P in one branch and Q in the other branch. Depending upon the conditions of the switches electricity can flow between the BATT and the BULB and make the BULB shine light. For this NOT to happen both switches must be open (Fig A00 at the bottom). Otherwise, if either switch is closed (Fig A10, Fig A01 middle two figures), or if both are closed (Fig A11 at the top), then electricity can go between BATT and BULB.
Again are the logical statements:
The adjoining figure Fig A shows four diagrams of a battery BATT and a light bulb BULB connected by a wire that has two branches (in parallel). In each branch is a switch, P in one branch and Q in the other branch. Depending upon the conditions of the switches electricity can flow between the BATT and the BULB and make the BULB shine light. For this NOT to happen both switches must be open (Fig A00 at the bottom). Otherwise, if either switch is closed (Fig A10, Fig A01 middle two figures), or if both are closed (Fig A11 at the top), then electricity can go between BATT and BULB.
Again are the logical statements:
p: electricity can flow through switch P,
q: electricity can flow through switch Q
The following statement is applied to each of these four situations:
electricity can flow between BATT and BULB
The last statement about some connected path between BATT and BULB is equivalent to saying
p or q
This says that switch P is closed or switch Q is closed (either p or q is true).
It must be assumed that this statement is true if either both p,q are true. The connective "or" is not exclusive; it allows both to be true. This physical model of switches suggests the following logic definition:
[2.5] Alternation An alternation is formed when the word "or" is placed between two logical statements. The alternation is false if and only if both logical statements are false.
Notation: The alternation p or q is false if and only if oth p and q are false.
Another notation for alternation is ∨: p ∨ q. In these volumes the English word will be used. Sometimes the symbol will be used to avoid confusion.
The logical statements p, q participate in the alternation p or q. They will be called (logical) participants
The alternation itself becomes a logical statement because definition [2.4] gives it a truth value.
If either p is false or q is false (or both are false) then p and q is false.
[2.6] The truth table for logical alternation
p q p or q
T T T
T F T (because of the last T here, alternation is different from just the second variable q)
F T T
F F F
[2.7] (Alternation is commutative) The truth value of an alternation is not changed if the logical participating statements are switched.
[2.8] (Extended logical alternation) Logical alternation can be extended to include more than two statements by placing the word "or" between the statements. The extended alternation is false if and only if all the logical statements in it are false
Notation: p or q or r or ... is false if and only if all statements p,q,r,... are false.
The truth table for an alternation of three variables has under the expression seven T's and a single F (See [2.5] above.)
In table [2.6] the T-F notation may be replaced by the 1-0 notation, and the connective "or" in the header, replaced by the sign of addition "+". However a problem arises when ordinary arithmetic addition is imposed. Click here for a discussion of Boolean arithmetic.
There is another logical connective, but it is not often used in these discussions nor in elementary books on logic. Click here for a discussion of joint denial.
Section 3 Logical Implication
It is a common form of mental activity to make a conclusion from conditions or available information. Even ancient man could look up at the darkening sky and then prepare for a storm. English has a common grammatical structure to indicate this process of deduction (or logical inference) in the form of "if-then." Two examples of this form are:
(I) if it is raining, then clouds are in the sky
(II) if John is in Canada, then John is in Paris (France)
Of these two compound statements, (I) is true, and (II) is false.
[3.1] (Implication) An implication involving two logical statements is formed when the word "if" is placed before the first statement, called the hypothesis and the word "then" is placed between the two statements, before the second statement, called the conclusion. The implication is false if and only if the hypothesis is true and the conclusion is false.
Notation: hypothesis → conclusiuon (the arrow always points from the hypothesis toward the conclusion)
In symbols, p → q is false if and only if p is true and q is false.
The logical statements p, q participate in the implication p → q. They will be called (logical) participants
The implication itself becomes a logical statement because definition [3.1] gives it a truth value.
This form if p then q has two parts, p is called the hypothesis and q, is the conclusion. The hypothesis p and conclusion q are themselves logical statements.
The form if p then q can be restated as p implies q
(I) can be restated as: it is raining implies clouds are in the sky.
The connective implies suggests the name (logical) implication.
An implication has the notation:
if p then q;
p implies q
p → q
A necessary condition for p is q
A sufficient condition for q is p
[3.2] (Truth table for implication) A truth table for implication p → q:
p q p → q
T T T
T F F
F T T (because of this last T, an implication is not logically the same as an equivalence)
F F T
The following statements about truth values for implications are based on [3.2] and on [3.1]:
[3.3a] An implication is itself false only if the hypothesis is true and the conclusion is false.
[3.3b] An implication with a false hypothesis is always true.
[3.3c] In a true implication, a true hypotheses always guarantees a true conclusion. (logical deduction)
By [3.3b] the implication 4=5 implies q is true, even if the truth value of q is not known.
[3.4] (Implications are reflexive) Every logical statement implies itself.
p → p
The implication p → p is always true, because it is impossible for the hypothesis p to be true and the conclusion p to be false. The variable p cannot be both true and false at the same time.
Notice that this is a proof without resort to a truth table.
The following fact is very useful in many arguments and proofs. Its name comes from a simple portable telescope, after extended use, it is folded into a smaller, compact form for storage.
[3.5] (Telescoping implications; transitive property) If a first logical statement implies the second, and the second in turn implies the third, then the first logical statement implies the third.
Notation: For any logical statements p,q,r if (p → q) and (q → r) then p → r.
This statement is true for any truth values of the variables. The parentheses indicate that the implications inside are evaluated first, and then the conjunction "and" between the implications is evaluated afterwards.
A truth table with 8 columns will be used to prove [3.5]. The expressions in parentheses indicate which columns to the left are used to get truth values.
1 2 3 4 5
6
7
8
(1+2)
(2+3)
(4+5)
(1+3)
(6+7)
p q r p → q q → r
(p → q) and (q → r) p → r
(6) implies (7)
T T T T T
T
T
T
T T F T
F
F
F
T
T F T F T
F
T
T
T F F F T
F
F
T
F T T T T
T
T
T
F T F T F
F
T
T
F F T T T
T
T
T
F F F T T
T
T
T
It is important to remember the only way that an implication can be false: the hypothesis is T but the conclusion is F. In all other situations, the implication is true. These facts are used to get truth values for columns 4,5,7 and 8. The truth values for column 6 are determined by the definition of a conjunction: a conjunction is T if and onliy if both participating statements are T Otherwise the conjunction is false. The truth values in column 8 are obtained by looking at columns 6 and 7. The fact that column 8 has no F's means that the expression under 6 does imply the expression under 7 for all possible truth values of p,q,r. This proves [3.5].
A related proof will be discussed in section 4. Click here to see that related proof as an evaluation of a logical expression. Also a link to an indirect proof will be given there. Click here to see that indirect proof.
Sometimes the telescoping effect involves more than three logical statements.
[3.6] (Chain of telescoping implications) Suppose all the implications
p → q1, q1 → q2, ..., qn-1 → qn, qn → r
are true. Then the implication p → r is true.
In many proofs, an implication is proven true by means of a chain of true implications.
[3.7] (Converse of an implication) The converse of an implication is obtained by interchanging the hypothesis and conclusion.
Notation: The implication q → p is the converse of the implication p → q.
Sometimes that same converse is written p ← q, which also makes q the hypothesis.
Examples:
The true implication x+1 = 7 → x=6 has a true converse x=6 → x+1 = 7.
The true implication John is in New York → John is in the USA has a false converse John is in the USA → John is in New York.
The examples show that the converse of a true implication may be true or it may be false. There is no guarantee that the converse of a true implication will be true.
In English there are a number of expressions that are equivalent to the implication p =→ q:
p implies q
the truth of p guarantees the truth of q
from p it follows that q
from p one can deduce q
q if p
p only if q
a sufficient condition for q is p
a necessary condition for p is q
An important situation happens when both an implication and its converse is true.
[3.8a] (Equivalence through implications) If two logical statements imply each other then they are equivalent.
Notation: if (p → q) and (q → p) then p ←> q .
Under the condition and p,q (truly) imply each other, it is impossible that they have opposite truth values, because otherwise one of the implications would have a true hypothesis and a false conclusion. This is not allowed for any true implication.
[3.8b] (Equivalence as two implications) Two equivalent logical statements imply each other.
Notation: if p ←>q then (p → q) and (q → p).
This statement is trivial. Because p is equivalent to q, then p and q have the same truth value. Then each implies the other, because one cannot be true and the other false.
This suggests that the sign (↔) for equivalence is made up of two arrows (→ and ←).
Section 4 Evaluating and Comparing Expressions
Algebraic quantities or expressions are familiar ideas:
7 + 5 = 12, x2 + 4x + 6, 1/y, x + 2y - 3z
are expressions in 0,1,2 and 3 variables respectively. Similarly,
"The equator is halfway betwen the North Pole and the South Pole" ~p, p → q, p and q and r and "1+3=4"
are logical expressions in 0, 1, 2, and 3 variables. Those statements and variables participate in the expressions. Intuitiveliy speaking, almost anything with truth value is a logical expression. Therefore, a logical expression has all the properties of a logical statement. Often its participating logical variables have unknown truth values. Therefore, like a truth table for variables, a table of possibilities can be made and the expression evaluated for each possibility.
Expressions can contain participating expressions, which in turn can contain participating expressions etc. The expression
(*) ~p or ~q
is an example. This alternation is made up from the expressions ~p, ~q. Truth values assigned to p,q inturn assign truth values to the expressions ~p,~q, which assign truth values to the expression (*). .
Parentheses are used in algebra and arithmetic to indicate what operations are done before other operations. Arithmetic operations inside parentheses are done before operations outside of the parentheses. Therefore the expression 4(3 + 2) is equivalent to 4x5 which is equal to 20. Without the parentheses the multiplication is done before the addition. So that the expression is then equivalent to 4x3 + 2 which is equal to 14. A similar law of precedence holds true in logic. For the evaluation of the expression
p and (q or r)
in a truth table the evaluation of the alternation "or" is done before the conjunction "and". For the evaluation of
(p and q) or r
the evaluation of the conjunction "and" is done before the evaluation of the alternation "or". For a complete evaluation of these two expressions click here. It shows that the two expressions are not logically equivalent. This means that the location of parentheses in any logical expression is important.
In these discussions evaluations of relatively simple expressions will be made or indicated. More complicated expressions are studied in advanced courses in mathematical logic. In some cases computers can be programmed to do the evaluation.
A major task of logic is the evaluation and then comparison of expressions with participating variables. In most cases equivalence or implication will be used in making the comparison. Perhaps one expression implies the other, or one expression is equivalent to the other. A simple example of equivalence is the proof of the following by a truth table.
[4.1] (Double negative) The denial of the denial of a logical statement is logically equivalent to that logical statement itself.
Notation: ~~p ↔ p.
This is expected. In algebra a double negation is actually a positive: -(-x) = x for every number x.
Truth table for ~~p (an intermediate step ~p is used):
p ~p ~~p
T F T
F T F
~p has the opposite truth values of p. ~~p has the opposite truth values of ~p. As a result, p and ~~p have the same truth values for all (both) possibilities. The columns of truth values under p and under ~~p are identical. By [1.2] this proves that p and ~~p are equivalent for all possibilities.
For example, the denial that "Washington is not in the USA" is equivalent to saying that "Washington is in the USA". To say that it is false that "2 + 3 is not equal to 5" is equivalent to saying that "2 + 3 equals 5".
Curiously, the grammars of some languages like Spanish and Russian allow a double negative to be equivalent to a single negative.
Obviously an odd number of negative signs produces a logical statement equivalent to the negative of an original statement. An even number produces a logical statement that is equivalent to an original statement.
~ ~ ~ ~ ~p ↔ ~p (odd number of tildas) ~ ~ ~ ~ ~ ~ ~ ~p ↔ p (even number of tildas)
In many discussions the expressions involve more than one variable. They may involve conjunction, alternation, implication, equivalence and negation and a mixture of them. For example, (p and q) or ~(p → q) or q is a logical expression of two variables. It has a truth value for each of the four possibilities for p,q.
There are expressions that are true for all possibilities for the logical variables that are participating in the expressions. For example, the expression p or ~p is true for both truth values of p. Similarly, the equivalence in the expression (p and q) ↔ (q and p) is always true.
[4.2] (Tautology) A logical expression is a tautology if it is true for all possible truth values for all logical variables participating anywhere in the expression.
Intuitively speaking, in a truth table for evaluating the expression, a column of T's with no F's appears under the logical expression.
Therefore, two expressions expression1, expression2 are equivalent if and only if the expression with the equivalence expression1 ↔ expression2 is a tautology. (The equivalence mentioned in [4.1] is a tautology.) Similarly, expression1 implies expression2 if and only if the expresseion with the implication expression1 → expression2 is a tautology.
For example, the following truth table shows that the implication (p and q) → (p or q) is a tautology:
1 2
3 4 5
p q p and q p or q (p and q) → (p or q)
T T
T
T
T
T F
F
T
T
F T
F
T
T
F F
F
F
T
Truth values in columns 1 and 2 determine the truth values in column 3 and in column 4 (See the truth tables for conjunction and alternation). But the truth values in collumn 3 and column 4 determine the truth values in column 5, according to the implication 3 → 4. The only T in column 3 is at the top, and there is a T at the top of column 4. The rest of truth values in column 3 are F's which always make true implications 5. So only T's are in column 5. The implication is a tautology.
[4.3] a conjunction of two logical statements always implies the alternation of those two logical statements.
The statement [4.3] can be extended to any number of logical statements.
Notation: (p and q and r and ...) → (p or q or r or ...) .
In truth tables the possibilities listed in [1.4],[1.5],[1.6],... will be used. In fact these might be omitted but their sequences will still be understood. For example, the following is a truth table listing the truth values for the four expressions, that are conjunction [2.2], alternation [2.6], implication [3.2] and equivalence [1.10] (the numbers above them will be used for reference):
[4.4]
3
4
5 6
p and q
p or q
p → q
p ↔ q
T
T
T T
F
T
F F
F
T
T F
F
F
T T
It is convenient to state the equivalence of expressions that applies to truth tables.
[4.5] (Equivalent expressions) Two logical expressions are equivalent if they have the same column of truth values under them in a truth table.
Obviously, [4.4] shows no equivalence among the four expressions.
However, there is a situation of one expresssion implying the other. But first a clarification.
[4.6] (Implications involving expressions) A logical expression1 implies a logical expression2 if for no possibility is there a T under expression1 and an F under expression2.
Let expression1 = p and q, expression2 = p or q in table [4.4]. The following is the truth table for these expressions:
3 4
p and q
p or q
T T
F T
F T
F F
There is no T under (3) with an F under (4) in the same horizontal row. Therefore conjunction implies alternation:
p and q → p or q
This means that in these discussions the "inclusive or" is used. The connective "and/or" can be simply written as "or".
Suppose expression1 and expression2 involve variables p and q. A truth table can be constructed containing the four possibilities for the variables:
[4.7] Form of a truth table for evaluating two expressions with variables p and q
p q
expression1
expression2
T T
?
?
T F
?
?
F T
?
?
F F
?
?
The question marks represent unknown truth values. They become known when the expressions are evaluated. For example, the table of comparisons for implication and its converse is:
p q
p → q
p ← q
T T
T
T
T F
F
T
F T
T
F
F F
T
T
Because of the different columns of truth values under the two expressions, the two expressions are not equivalent.
Now put a connective "and" between the implication to receive a compound expression1. Construct a truth table for the expression 1:
p q
(p → q) and (p ← q)
The parenthes indicate that what is in side them must be evaluated first. Therefore expand the header to:
3
7
8
(p → q) (p ← q)
(p → q) and (p ← q)
T
T
T
F
T
F
T
F
F
T
T
T
The expressions 3 and 7 have already been evaluated in a previous table above.
The truth values in column 8 are determined by the truth values in columns 3 and 7 and the truth values for conjunction.
The truth values in column 8 are those for equivalence [1.10]. Attaching that column as column 6 to this table produces the following:
1 2
8
6
p q
(p→q) (p←q)
(p→q) and (p←q)
p ↔ q
T T
T
T
T F
F
F
F T
F
F
F F
T
T
The columns 8 and 6 of truth values are identical. Therefore the expressions 8 and 6 are equivalent. This can be expressed as a useful theorem, replacing variables p,q by expressions:
[4.8] Each of two expressions implies the other if and only if they are equivalent.
Reading expression 6 first and then expression 8 supports the following:
[4.9] Equivalent expressions imply each other.
Previous tables show that an implication and its converse are not equivalent. The hypothesis may be false and the conclusion true, making the implication true and the converse false. With an implication and its contrapositive, the situation is different.
[4.10] (The contrapositive) The contrapositive of an implication is obtained by interchanging and negating the hypothesis and conclusion
The contrapositive of p→q is ~q→~p
[4.11] Any implication and its contrapositive are logically equivalent.
Notation: p → q is equivalent to ~q → ~p
Examples:
implication
contrapositive
p → q
~q → ~p
If it is raining, then clouds are in the sky
if clouds are not in the sky, then it is not raining
If John is in Washington, then John is in the USA
if John is not in the USA, then John is not in Washington
Click here to see a proof of [4.11] by truth table.
In the following, the statements p,q may be replaced by expression1, expression2 respectively.
[4.12] Two methods to prove that a statement q is true.
(a) Direct proof
Find a statement p that is known to be true (or it can be assumed).
Prove that the implication p → q is true, usually by a chain of implications.
(b) Indirect proof
Form the denial of q, which is ~q.
Prove that the implication ~q → ~p is true, usually by a chain of implications, and arrive at a statement ~p that is known to be false.
The following is a list of logical formulas for reference. A few examples from algebra are shown here. But the best examples of these formulas (and the corresponding formulas for open statements) are found in the discussions in the next chapter, Chapter 2. The variables p,q,r below may be replaced by expression1, expression2, expression3
The connectives in red are always true (tautologies).
[5.1] Two valued logic:
[a] p and ~p is always false. This may be expressed as
~(p and ~p)
[b] p or ~p
[5.2] Distributive laws:
[a] p and (q or r) is equivalent to (p and q) or (p and r)
[*]
x(y + z) = xy + xz
[b] p or (q and r) is equivalent to (p or q) and (p or r)
[5.3] Transitive law/ Telescoping (Reduction) of a chain of implications:
if (p → q) and (q → r)
then (p → r)
[5.4] Replacement of equivalence by implication
[a] if (p ↔ q)
then (p → q)
[b] if (p ↔ q)
then (p ← q)
[5.5] Implication in the form of an alternation:
p → q is equivalent to ~p or q
[5.6] Negation of expressions:
[a] ~~p is equivalent to p
Double negation is positive
[b] ~(p and q) is equivalent to ~p or ~q
DeMorgan's law
[c] ~(p or q) is equivalent to ~p and ~q
[d] ~(p → q) is equivalent to p and ~q
[5.20] Fundamental properties of conjunction
[*]
[a] p and q is equivalent to q and p
commutative
[b] p and p is equivalent to p
idempotent
[c] if p and q then p
[d] if p and q then q
[e] if (r → p) and (r → q)
then
r → (p and q)
combine conclusions
[5.25] Fundamental properties of alternation
[*]
[a] p or q is equivalent to q or p
commutative
[b] p or p is equivalent to p
idempotent
[c] if p then p or q
[d] if q then p or q
[e] if (p → r) and (q → r)
then
(p or q) → r
combine hypotheses
[5.30] Three distinguishing properties of equivalence:
[*]
[a] p is equivalent to p
reflexive:
[b] p ↔ q is equivalent to q ↔ p
symmetric
[c] if (p ↔ q) and (q ↔ r)
then (p ↔ r)
transitive
[5.35] Logical inference, ways of proving the truth of q:
[*]
[a] if p and (p → q) then q
direct proof of q
[b] if (~q → ~p) and p then q
indirect proof of q
[c] if (p or q) and ~p
then q
proof of q by elimination
[5.40] Proving an equivalence by proving an implication and its converse:
if (p → q) and (q → p)
then (p ↔ q)
 The adjoining figure Fig A shows four diagrams of a battery BATT and a light bulb BULB connected by a wire that has two branches (in parallel). In each branch is a switch, P in one branch and Q in the other branch. Depending upon the conditions of the switches electricity can flow between the BATT and the BULB and make the BULB shine light. For this NOT to happen both switches must be open (Fig A00 at the bottom). Otherwise, if either switch is closed (Fig A10, Fig A01 middle two figures), or if both are closed (Fig A11 at the top), then electricity can go between BATT and BULB.
Again are the logical statements:
The adjoining figure Fig A shows four diagrams of a battery BATT and a light bulb BULB connected by a wire that has two branches (in parallel). In each branch is a switch, P in one branch and Q in the other branch. Depending upon the conditions of the switches electricity can flow between the BATT and the BULB and make the BULB shine light. For this NOT to happen both switches must be open (Fig A00 at the bottom). Otherwise, if either switch is closed (Fig A10, Fig A01 middle two figures), or if both are closed (Fig A11 at the top), then electricity can go between BATT and BULB.
Again are the logical statements:
 An electrical switch either allows electricity to pass through (it is on, it is closed) or it prevents electricity from passing through (it is off, it is open). The adjoining figure Fig C shows four diagrams of a battery BATT and a light bulb BULB connected by a wire that has two switches P and Q (in series). Depending upon the conditions of the switches electricity can flow between the BATT and the BULB and make the BULB shine light. For this to happen both switches must be closed (Fig C11 at the top). Otherwise, if either switch is open (Fig C10, Fig C01 in the middle), or if both are open (Fig C00 at the bottom), then electricity cannot go between BATT and BULB.
An electrical switch either allows electricity to pass through (it is on, it is closed) or it prevents electricity from passing through (it is off, it is open). The adjoining figure Fig C shows four diagrams of a battery BATT and a light bulb BULB connected by a wire that has two switches P and Q (in series). Depending upon the conditions of the switches electricity can flow between the BATT and the BULB and make the BULB shine light. For this to happen both switches must be closed (Fig C11 at the top). Otherwise, if either switch is open (Fig C10, Fig C01 in the middle), or if both are open (Fig C00 at the bottom), then electricity cannot go between BATT and BULB.