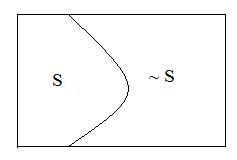
 Let S be any set in a universe U. Collect all objects outside of S to form a new set ~S. For example, in the universe N9 let S = {1,3,5,7,9} then ~S = {2,4,6,8}.
Let S be any set in a universe U. Collect all objects outside of S to form a new set ~S. For example, in the universe N9 let S = {1,3,5,7,9} then ~S = {2,4,6,8}. In the adjacent figure all of the points outside area S form a set ~S.
[1.1] A set in a universe is a collection of objects that belong to that universe. It is also called a subset of that universe. (The collection may be made by selecting objects from all the objects in the universe. But nothing is removed from the universe.)
(Numerical) Example 1: In the universe N9 make a random collection of numbers, say 6,2,8,5 and then together they form the set {6,2,8,5}. But for convenience the numbers inside the set notation { } are usually listed in increasing order: {2,5,6,8}.
(Numerical) Example 2: In the universe N9 collect the numbers between 3 and 8. This collection becomes the set {4,5,6,7}. But this set is also the truth set of the open statement
 (Geometric) Example 3: In the adjacent figure the universe is all points inside the rectangle. The set is the interior of the circle. If c is the center and ρ (Greek letter rho) is the radius then this interior is also the truth set of the open statement
(Geometric) Example 3: In the adjacent figure the universe is all points inside the rectangle. The set is the interior of the circle. If c is the center and ρ (Greek letter rho) is the radius then this interior is also the truth set of the open statement
Let subset S be the collection of all selected objects in a universe U. Two extremes are allowed. All objects in U may be selected Then S = U. Therefore, any universe is a subset of iteself. It may also happen that all objects in U are rejected. Then S is empty, S = Φ. Therefore the empty set Φ is a subset of any universe.
To distinguish selected objects from rejected objects in a universe, it may be useful to assign a T to each selected object, and an F to each rejected object. This allows open statements to do selections done in most of the following discussion. Then the truth sets of the open statements form the subsets of the universe. Conversely, for any subset S the open statement
[1.2] (Relationship between sets and open statements)
(a) Every open statement determines a subset of its universe, namely its truth set.
(b) For every subset of a universe there is an open statement whose truth set equals that subset.
For any set S in a universe U there are many open sets p(x), q(x), r(x), ... whose truth sets equal S. For example:
The following "set builder notation" denotes the truth set of an open statement p(x) with universe U:
 Let S be any set in a universe U. Collect all objects outside of S to form a new set ~S. For example, in the universe N9 let S = {1,3,5,7,9} then ~S = {2,4,6,8}.
Let S be any set in a universe U. Collect all objects outside of S to form a new set ~S. For example, in the universe N9 let S = {1,3,5,7,9} then ~S = {2,4,6,8}.
In the adjacent figure all of the points outside area S form a set ~S.
[2.1] (Complement) The complement of a set in a universe is the collection of all objects in the universe that are not in the given set.
Notation: ~S = {x in U | x is not in S}.
Notation: In a universe U, x is in ~S if and only if x is not in S.
If a tilda (~) is "attached" to a set symbol S then the complement ~S of that set is formed. Therefore the tilda (~) is a unary operation on individual sets that forms their complements.
It is obvious that the complement of ~S must be S which contains all objects in the universe not in ~S. Therefore, the complement of the complement of a set is the set itself. ~ ~S = S.
Another notation for complement is U\S (a special form of set subtraction defined in [2.12] below). This notation indicates the need for knowing the universe U in order to determine the complement of S.
If S is empty then ~S must be the entire universe, because no object in the universe can be selected to be in S. Therefore, every object is not in S and must be in ~S. U\Φ = U. The complement of the empty set is the entire universe.. Similarly, the complement of the universe is the empty set: U\U = Φ.
-----
A binary operation accepts two things and produces a third thing. For example, the arithmetic operation of addition accepts 3 and 5 and produces 8. The operation of multiplication accepts 3 and 5 and produces 15. Each operation here accepts two sets, often designated as S1, S2, and produces a set from them. To emphasize coordination with circles in geometric models the sets
S1, S2 may be in colors. Then they denote the interiors of
red, blue circles. Colors may also be used for sets in N5 and N9.
In any case, there are two trivial open statements
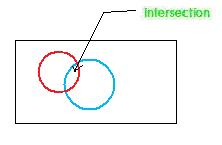
The intersection of streets is that portion common to both streets.The adjacent figure shows the intersection of the interiors of a circle and another circle.
[2.2] (Intersection) The intersection of two sets in the same universe consists of all objects that are in both sets.
Notation1: S1 /\ S2 = {x in U | x is in S1 and x is in S2}.
Notation2: x is in S1 /\ S2 if and only if x is in S1 and x is in S2 (a true statement about universally true equivalence)
The common notation for intersection is an upside down U:
But for typographical reasons, the notation /\ will be used in all volumes to denote intersection.
Example: In N9 the intersection {2,3,4,5,6} /\ {4,5,6,7,8} = {4,5,6}. Simply go through the two sets {2,3,4,5,6}, {4,5,6,7,8} and select those numbers in both sets:
It is instructive to see the formation of the intersection using truth values. Every number in N9 receives two truth values from the open statements
From the wording of definition [2.2] it is obvious that the intersection of two sets is the same no matter which set is written first.
[2.3] (Commutativity) The operation of intersection is commutative.
Notation: S1 /\ S2 = S2 /\ S1.
But what happens to the intersection if one or both sets are empty? For example, what is the intersection {2,3,4,5,6} /\ Φ? The open statements
In general, if either of two sets is empty then their intersection is empty: S /\ Φ = Φ,
Φ /\ S = Φ, Φ /\ Φ = Φ
By definition, the open statement x is in Φ is universally false. Therefore, any conjunction involving that phrase will have to be universally false.
The intersection of any set and the universe is equal to that set:. S /\ U = S, U /\ S = U, U /\ U = U
Click here to see the an argument supporting this statement.
Intersection of sets has a relationship to nmultiplication of numbers. Click here to see a discussion about this relationship.
The intersection of more than two sets is defined in the obvious way:
[2.4] The intersection of sets in the same universe consists of all objects that are in all the given sets
Notation: x is in S1 /\ S2 /\ S3 /\ ... if and only if x is in S1 and x is in S2 and x is in S3 and ...
Parentheses surround an operation to be done first. Short arguments can be made to support the two equalities
[2.5] (Associativity) The operation of intersection is associative.
Notation: (S1 /\ S2) /\ S3 = S1 /\ (S2 /\ S3).
-----------------------
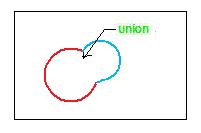
The adjacent figure shows the union of a set and another set. It is the combined interiors of the two sets, including their intersection if they overlap.
[2.6] (union) (In the same universe) the union of two sets is the collection of all objects in either set (or both)
Notation: x is in S1 \/ S2 if and only if x is in S1 or x is in S2 (or x is in both sets).
The common notation for union is a U:
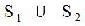
But for typographical reasons, the notation \/ will be used in all volumes to denote union.
Example: {2,3,4,5,6} \/ {4,5,6,7,8} = {2,3,4,5,6,7,8} universe U = {1,2,3,4,5,6,7,8,9} because
x is in {2,3,4,5,6,7,8} if and only if x is in {2,3,4,5,6} or x is in {4,5,6,7,8}
There are three open statements here:
From the notation following [2.6] it obvious that that an alternation of open statements determines the union of sets. And in doing so, it shows how a union assigns truth values to each object in the universe:
It is sometimes useful to look negatively at a union of two sets. The following is actually equivalent to [2.6] (see [5.6c] in Vollume A, chapter 1):
[2.7] (Not in a union) In a common universe, an object is not in the union of two sets if and only if that object is in neither set.
Notation: x is not in (S1 \/ S2) if and only if x is not in S1 and x is not in S2.
Click here for a discussion of duality between intersection and union.
From the wording of definition [2.6] it is obvious that the collection of objects from both unions S1 \/ S2 and S2 \/ S1 are the same. In other words, the open statements
[2.8] (Commutativity) The operation of union is commutative.
Notation: S1 \/ S2 = S2 \/ S1.
But what is the union {2,3,4,5,6} \/ Φ involving the empty set? The open statements
If 1 represents the universe U and 0 represents Φ then the representations of the four intersections of these two sets produce a strange (Boolean) addition table for 1 and 0. Click here to see this discussion.
The union of more than two sets is defined in the obvious way.
[2.9] The union of sets in the same universe consists of all objects that are in any the sets
Notation: x is in (S1 \/ S2 \/ S3 \/ ...) if and only if x is in S1 or x is in S2 or x is in S3 or ...
It is sometimeds useful to discuss oobjects not in the union of two sets. It is a form of De Morgan's law.
[2.10] (Outside a union of sets) An object is not in a union of sets all in the same universe if and only if that object is in none of the sets.
Notation:
x is not in S1 \/ S2 \/ S3 \/ ... if and only if
all the open statements x is in x is in S1 or x is in S2 or x is in S3 or ...
Short arguments can be made to support the two equalities
[2.11] (Associativity) The operation of union is associative.
Notation: (S1 \/ S2) \/ S3 = S1 \/ (S2 \/ S3).
------
Occasionally useful is a type of subtraction of sets. It is a generalization of the idea of complement [2.1]. A superset replaces the universe. The back slash (\) is used again.
[2.12] (Set difference) The set difference between a second set and a first set is the collection of all objects in the first set that is not in the second set.
Notation: x is in (S1\ S2) if and only if x is in S1 and x is not in S2.
Intuitively speaking, the second set takes away objects from the first set. Also, it is the remaining part of the first set after the intersection of the two sets is removed.
Example: Let N9 be the universe.
As expected, S\Φ = S because nothing is being taken away from S.
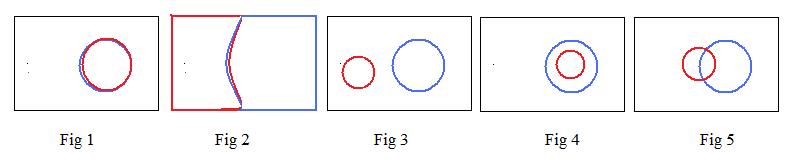
Any object in the universe that makes a relation between sets false is called a counterexample to the relation.
Sets are determined by the objects in them. The sets S1 and S2 are truth sets of the trivial open statements
[3.1] (Equality of sets) Two sets in the same universe are equal if and only if they contain exactly the same elements.
Notation 1: S1 = S2 if and only if the open statements x is in S1, x is in S2 assign equal truth values to each object in the universe.
Notation 2: S1 = S2 if and only if the equivalence x is in S1 <==> x is in S2 is universally true.
Example: In universe N9, {5,7,6,8,4} = {4,5,6,7,8} because they contain exactly the same numbers. Any number in N9 is in both of them (is assigned TT) or it is in neither of them (is assigned FF). But notice that this shows the listing of the objects in a set can be written in different arrangements of the same objects (permutations).
Click here to see a discussion supporting the fact that all empty sets are equal. In other words, in any universe there is only one empty set. It is unique.
---------
For equality (&&) assignes equal truth values to each object in the universe. The other extreme is that (&&) assigns opposite truth values.
But this means that each set is the complement of the other.
[3.2] (Complementary sets) Two sets inside the same universe are complementary if and only if one is the complement of the other.
In Fig 2, S2 contains everything not in S1 and conversely. Every object in the universe is assigned a pair of different truth values: TF or FT from the open sets in (&&).
Inside the universe N9 the two sets {1,3,5,7,9} and {2,4,6,8} are complementary. It is obvious that the complement of the complement of a set is that set. Click here for a discussion supporting this statement.
[3.3] Two sets in the same universe are complementary if and only they satisfy both both of the following conditions:
(a) their union is the universe;
(b) their intersection is empty.
Notice that {1,3,5,7,9} /\ {2,4,6,8} = Φ and that {1,3,5,7,9} \/ {2,4,6,8} = N9, the universe.
Click here for a discussion supporting [3.3].
------
Relax condition (a) in [3.3] to get a more general situation as shown in Fig 3. The two sets do not overlap. There is nothing in their intersection. No point in the universe can be assigned TT by the open statements (&&). However if their union is not the entire universe then some objects outside the union will be assigned FF.
[3.4] (Disjoint sets) In the same universe a pair of sets are disjoint if and only if their intersection is empty
Notation: S1, S2 are disjoint if and only if the open statements
A pair of complementary sets are always disjoint, but not conversely. Fig 3 shows disjoint sets that are not complementary.
-------
Fig 4 shows an important situation: all of one set may be part of another set.
This means that all the points in first set are also in the second set.
[3.5] (Inclusion) One set is included in a second set if and only if every object in the first set is also in the second set.
Notation: S1 < S2 if and only if x is in S1 => x is in S2.
If one set is included in a second set then the first set is called a subset of the second set. Obviously, every set in a universe is a subset of that universe.
Example: Let the universe N9 = {1,2,3,4,5,6,7,8,9}.
It is obvious that {4,5,6} is included in {3,4,5,6,7,8}. Also the implication
If two sets are equal then the content of either set is included in the other. If one set is equal to a second set then the first set is included in the second set. The underline in the notation < allows inclusion to extend to equality:
The reverse of inclusion is containment.
A set S2 contains a set S1 if and only if S1 is included in S2
Notation: S2 > S1
If one set contains another then the first set is sometimes called a superset of the second set.
If S1 = S2 then trivially everything in S1 is in S2. Therefore every set is included it itself. It is a subset of itself.
The symbol < is used in these discussions to mean inclusion but not equality. It is called strict inclusion. The statement
There is also strict containment, S2 > S1. In this situation S2 contains all of the objects in S1 plus one or more objects not in S1. The statement
[3.6] (Summary of sets and associated open statements)
From sets S1, S2 to associated open statements p(x), q(x): any open statement equivalent to x is in S1, x is in S2 respectively.
From open statements p(x), q(x),\ to sets S1 = truth set of p(x), S2 = truth set of q(x).
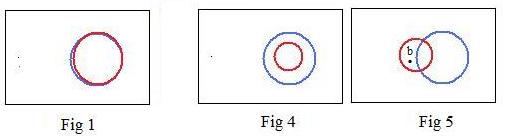
In Fig 4 and Fig 1, set S1 is entirely inside set S2. But in Fig 5, set S1 is not entirely inside set S2. Part of S1 lies outside of S2. There are points in that part. Any of those points is called a counterexample to the inclusion S1 < S2. If point b is one of those counterexamples, then (&&) assigns truth values TF to point b. That point b is also a counterexample to (the universality of) the implication
The following is seemingly trivial yet sometimes is useful as a basis for arguments supporting inclusions and universally true implications of open statements.
[4.1] (Inclusion) One set is included in another if and only if there are no counterexamples to this inclusion.
Notation1: S1 < S2 if and only if there exists no object b such that b is in S1 and b is not in S2.
Notation2: S1 < S2 if and only if no object in the universe is assigned TF by the open statements x is in S1, x is in S2 respectively.
Example: Again let the universe be N9 = {1,2,3,4,5,6,7,8,9}.
A counterexample to {1,2,3,4} < {3,4,5,6,7,8} is 1. So is 2. Each is in {1,2,3,4} but not in {3,4,5,6,7,8}. The remaining numbers 5,6,7,8,9 in U do not qualify as counterexamples, because none of them are in {1,2,3,4}. Therefore, they cannot produce false components. The statement about inclusion {1,2,3,4} < {3,4,5,6,7,8} is false because there are counterexamples.
The following statement provides a useful method to prove two sets are equal.
[4.2] (Equality from reverse inclusions) If two sets are included in each other then the two sets are equal.
Notation1: if S1 < S2 and S2 < S1 then S1 = S2
Notation2: if p(x) ==> q(x) and q(x) ==> p(x) then p(x), q(x) are equivalent.
The inclusions if S1 < S2 and S2 < S1 prevent any object from being assigned TF or FT. Therefore every object is assigned equal truth values, TT or FF, which is what happens only with equal sets and their trivial equivalent open statements.
The implication q(x) ==> p(x) is called the converse of the implication p(x) ==> q(x). The converse of a (universally) true implication may or may not be (universally) true. For example, in universe N9, x <5 ==> x < 8 is universally true, but its converse x < 8 ==> x < 5 has a counterexample, namely 7. Upon substitution for x, 7 makes the hypothesis x < 8 true, but the conclusion x < 5 false.
Statement [4.1] can be used to prove that the empty set Φ is a subset of any set S in any universe U:
This argument uses a typical approach for denying the existance of a counterexample: assume that there is a counterexample and then arrive at an impossible situation because of that assumption. Such an argument is called an indirect argument.
Both the empty set and the set itself are called the trivial subsets of the set itself. Often they are less interesting than the other subsets.
It is true that 2 < 5. But it is also true that -5 < -2. Negation of numbers interchanges the sides of an inequality. (This can be proven by subtraction of the smaller number from the larger.)
It is obvious that if a first set is included in a second set, then objects outside of the second set must also be outside the first set. But being outside a set is the same as being in the complement of that set. Let the two sets be A and B. Then
[4.3] (Inclusion from complements) A first set is included in a second set if the complement of a second set is included in the complement of the first.
Notation1: if ~S2 < ~S1 then S1 < S2.
Notation2: if ~q(x) ==> ~p(x) then p(x) ==> q(x).
The implication ~q(x) ==> ~p(x) is called the contrapositive of the implication p(x) ==> q(x). It can be proven that an implication and its contrapositive always have the same truth value. Consider the implications
The following is a useful property of inclusions and implications of open statements. It presupposes all sets and open statements have the same universe.
[4.4] (Telescoping property of inclusions) In any universe, if a first set is included in a second set, and the second set is included in a third set, then the first set is included in the third set.
Notation1: if S1 < S2 and S2 < S3 then S1 < S3.
Notation2: if x is in S1 ==> x is in S2 and x is in S2 ==> x is in S3 then x is in S1 ==> x is in S3.
Notation3: for any open statements p(x), q(x), r(x) with a common universe, if the implications p(x) ==> q(x) and q(x) ==> r(x) are both universally true, then the implication p(x) ==> r(x) is universally true.
In notation2 there are three implications involved:
In notation3 let S1, S2, S3 be the truth sets of p(x), q(x), r(x) respectively. Then the three implications

Since the empty set Φ and the universe U are genuine subsets of U, then Φ and U may be members of some families of subsets of U.
In the universe of the plane of plane geometry straight lines are special sets of points. Therefore, any collection of straight lines is a family of sets. The familiar properties of straight lines can be restated as properties of this family. Click here for more discussion of this geometric family of straight lines.
-----
For any given set, there is a unique family of all subsets of that set. That family is called the power set of the given set. For example, all the subsets of S={1,3,5} are
[5.1] (Size of the power set) If a set has n objects then its power set has 2n subsets in it.
Examples: There are 23 = 8 subsets of {1,2,3}. There are 29 = 512 subsets of the set N9.
A discussion supporting this statement will be given in a later volume. The attempt to extend this statement to infinite sets like N leads to an interesting discussion of transfinite numbers.
Let the reader show that [5.1] is true even when the given set is empty.
-----
The idea of two disjoint sets may be extended to a family of sets.
[5.2] (Family of disjoint sets) In a family of disjoint sets, every pair of sets in that family are disjoint.
Example: In N9 if A={1,3,5}, B={2}, C={6,8}, D={4}, then {A,B,C,D} is a family of disjoint sets. The intersection of any pair of sets in this family is empty.

The interiors of all of the circles in the adjacent figure form a family of disjoint sets.
Another example, not shown here, is any family of parallel straight lines.
-----
 Consider blankets on a very large bed. to cover the entire bed it may require several blankets that may overlap. The bed is under the combined collection of blankets. A similar situation may exist for some given set in a universe. A set may be "covered" by other sets in that universe.
Consider blankets on a very large bed. to cover the entire bed it may require several blankets that may overlap. The bed is under the combined collection of blankets. A similar situation may exist for some given set in a universe. A set may be "covered" by other sets in that universe.
[5.3] (Family covering of a set) A family of sets covers a given set if and only if the given set is contained in the union of all sets in the family. The family is called a covering of the given set.
Notation: Family W covers set S if and only if S < union of all sets in W.
Example: In universe N9 let S = {4,5,9}, and let W be the family
It is quite possible that all the sets in a covering be disjoint. Then the family is called a disjoint covering of the set. The disjoint covering is a special family of sets. Intuitively speaking, the set is broken down into pieces which are subsets in the family.
[5.4] (Partitions) A partition of a set is a disjoint covering of the set by its own subsets.
In other words, a partition separates the entire given set into a family of disjoint subsets. The union of all those subsets is the given set. In the universe N9 an example of a partition of S = {2,3,4,5,6,7,8} is the family

The adjacent figure shows a partition of the interior of a circle into colored subsets (sub-arias).
Sometimes it is useful to partition a large set into a family of smaller subsets which can be more easily measured. Nothing is lost during the partitioning process. For example, suppose a large number of coins in a pile are to be counted. Partition the coins into several smaller piles. Have each of the smaller piles counted by different people. Add together the number of coins in each smaller pile.
Suppose family
Example: if
[5.5] (Telescoping sets) For a family of n increasing sets, the first set is included in the last set.
Notation1: if S1 < S2 < S3 < S4 < ... < Sn
then S1 < Sn.
Notation2: if p1(x) ==> p2(x) ==> p3(x) ==> ... ==> pn(x) then p1(x) ==> pn(x).
A discussion supporting this statement will be given later after a discussion of positive integers, in particular mathematical induction. But it is pattered after the supporting statements for [4.4].