Go to other chapters or to other volumes of math
Additional Material for this Chapter
Exercises for this Chapter
Answers to Exercises
Chapter 2
Sets and Open Statements
Section 1: Introduction
In these volumes the word object will have an extended meaning. It could be something physical, such as a person, a grain of sand, a small round ball, a building, ... . But it may also be something abstract, like a number 5 or a geometric point. Whatever it is, it is usually indivisible (exceptions in Section 5). Objects may be collected together: physically such as balls in a bag or abstractly, such as points on some straight line. All such collections will be called sets. (In advanced mathematics there are discussions about some not very "nice" collections which produce logical paradoxes, e.g. the Russel paradox. In these volumes there will be no such weird collections of objects!) Although no rigorous definition of a set is given here, some simple conditions may be imposed:
[1.1] (Definitive conditions for sets)
(a) An object is either in a set or not in a set.
(b) Two sets are equal if and only if they contain exactly the same objects.
Sometimes the phrase "is a member of" a set may be used instead of "is in" a set.
In Volume B (Numerical systems) are discussions about objects called natural numbers and their properties. They are the familiar numbers without end for counting:
1, 2, 3, 4, 5, 6, ......100, ...., 10000000,..... 19278498694373, .... -->
They are whole numbers, no decimals, no fractions, no negatives, no largest (always one bigger), and in these discussions, no zero.
Collections of these objects can be made. For example, the sets of the first 2,5,9 natural numbers are:
N2 = {1,2}, N5 = {1,2,3,4,5}, N9 = {1,2,3,4,5,6,7,8,9}
These three sets show two things:
(a) Some sets may be declared by listing all its objects in between symbols { }. To fulfil condition [1.1a] any object not in the listing is not in the set.
(b) Sets may have names. In this case they are N2, N5, N9.
The objects 3, 5, 6 are in N9. The objects 10, 11 are not members of N9.
The reader can easily determine what objects are in the sets N6, N100, Nn where n=7.
In these discussions the name of the infinite set of all natural numbers is N, N = {1,2,3,4,5,6,...............-->}.
It is not always necessary to give names to sets. For example the set of all prime numbers in N9is {2,3,5,7}.
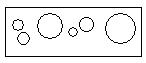
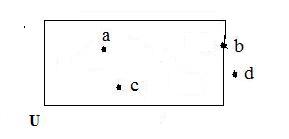 Usually all objects involved in a discussion form a collection called a universe. Objects outside a universe are ignored. Aninterior of a rectangle may serve as an example of a universe. Let its name be U. In the adjacent figure a,b,c,d are names of points. Points a,c are in U, and points b,d is not in U.
Usually all objects involved in a discussion form a collection called a universe. Objects outside a universe are ignored. Aninterior of a rectangle may serve as an example of a universe. Let its name be U. In the adjacent figure a,b,c,d are names of points. Points a,c are in U, and points b,d is not in U.
However, there may be more than one universe, often because some objects are very different from some other objects in the discussion. For example, a single discussion involves a universe of numbers and a universe of points. The discussion may relate the numbers to the points.
It is important to distinguish objects from the sets that objects are in. The object 1 is not the same as the set N1 = {1}.
------
Objects are inside universes. It is useful to consider a set inside a universe.
[1.2] A set inside a universe is a collection of objects that belong to that universe. It is also called a subset of that universe.
Below the letter S, sometimes with a numerical subscript, is used repeatedly as a name for some subsets in various discussions.
(Numerical) Example 1: The set {2,5,6,8} is a subset of the universe N9. But the set {5,7,100} is not a subset of N9 because 100 is not in the universe.
The collection of objects in a subset may be made by selecting objects satisfying some rule, from all the objects in the universe. (But nothing is removed from the universe.)
(Numerical) Example 2: In the universe N9 collect all the numbers between 3 and 8. This collection becomes the set {4,5,6,7}which is a subset of the universe N9.
 (Geometric) Example 3: In the adjacent figure the universe consists of all points inside and on the rectangle. The interior of the circle together with the circle itself is a subset of the universe. If c is the center then the subset consists of all the points whose distance from c is < the radius of the circle.
(Geometric) Example 3: In the adjacent figure the universe consists of all points inside and on the rectangle. The interior of the circle together with the circle itself is a subset of the universe. If c is the center then the subset consists of all the points whose distance from c is < the radius of the circle.
For any universe U, two extremes of selection are allowed:
(a) All objects in U are selected Therefore, every universe is a subset of iteself.
(b) No objects in U are selected. Then the subset is empty. It is given the permanent name Φ. The empty set Φ is a subset of every universe.
-----
Consider the following statements:
Table 1 (Components):
1 is between 3 and 8
2 is between 3 and 8
3 is between 3 and 8
4 is between 3 and 8
5 is between 3 and 8
6 is between 3 and 8
7 is between 3 and 8
8 is between 3 and 8
9 is between 3 and 8
All the statements are similar. Any of the nine statements can be reproduced by replacing the x in the single open statement
(*) x is between 3 and 8
by the (name of) any object in the universe N9. The nine statements are called components of the open statement (*).
Needed is a notation, called function notation, that is a name for the open statement displaying the variable:
p(x): x is between 3 and 8
x can be replaced by another vatriable, say y or z:
p(y): y is between 3 and 8
p(z): z is between 3 and 8
and also by (names 0f) objects in the universe N9. But these display the components:
p(1): 1 is between 3 and 8
p(2): 2 is between 3 and 8
......
p(9): 9 is between 3 and 8
Therefore, the nine components of p(x) are p(1), p(2), ..., p(9).
 Referring to the adjacent figure, let q(y) the open statement
Referring to the adjacent figure, let q(y) the open statement
q(y): point y is inside the circle
It is impossible to list all of the components of q(y) because there are infinitely many points in the universe (inside the rectangle). But four components can be displayed because four points have names a,b,c,d:
q(a): point a is inside the circle
q(b): point b is inside the circle
q(c): point c is inside the circle
q(d): point d is inside the circle
[1.3] (Open statements and components) An open statement in a variable with universe is a form in which if the variable is replaced by (the name of) any object in the universe, then the open statement becomes a logical statement, called a component of the open statement.
Notation: if p(x) is an open statement in x with universe U and b,c,d are (names of) objects in U, then p(b), p(c), p(d),... are logical statements derived from p(x) by replacing x by b, or x by c, or x by d.
Since components are logical statements they must have truth values. However, open statements do not have truth values. A componemt be true (T) or false (F). But objects produce these components upon substitution in the open statement. Table 2 displayes the function notation, the open statement, its components and truth values of the components
Table 2:
p(x): x is between 3 and 8. p(x) has no truth value
p(1): 1 is between 3 and 8. p(1) is F
p(2): 2 is between 3 and 8. p(2) is F
p(3): 3 is between 3 and 8. p(3) is F
p(4): 4 is between 3 and 8. p(4) is T
p(5): 5 is between 3 and 8. p(5) is T
p(6): 6 is between 3 and 8. p(6) is T
p(7): 7 is between 3 and 8. p(7) is T
p(8): 8 is between 3 and 8. p(8) is F
p(9): 9 is between 3 and 8. p(9) is F
Taken from the last column of the above table, Table 3 shows the truth values assigned directly to the objects:
Table 3:
1 F 2 F 3 F 4 T 5 T 6 T 7 T 8 F 9 F
[1.4] (Open statements giving truth values to objects) A open statement with a universe assigns a truth value to each object in that universe by copying the truth value of the component containing that object.
The open statement
x + 1 is between 4 and 9
with universe N9 also produces Table 3. Logic is interested only in the objects and truth values assigned to them, not in the method of assignment. This leads to the idea of logical equivalence.
There are different methods for asigning truth values to every object in some universe. One method is by selection. If an object is selected, assign a T to it. If rejected, assign an F. Different open statements also assign truth values to every object. Two methods for assigning truth values to all objects in a universe are logically equivalent if and only if they assign equal truth values to each object. In particular, this applies to open statements.
[1.5] (Equivalent open statements) Open statements with the same universe are logically equivalent if and only if they all assign equal truth values to each object in the universe.
The word "logically" often will be omitted.
The assignment of truth values to all objects in a universe can be done by selection. If an object is selected, assign a T to it. If rejected, assign an F.
If all the objects in a universe have been assigned truth values, then all those objects assigned a T form a distinguished set, called truth set. When open statements are equations, the truth sets are often called the solution sets. For example, the solution set of
3 < x < 8
is {4,5,6,7}.
The following "set builder notation" denotes the truth set of an open statement p(x) with universe U:
{x in U | p(x)}
Intuitively speaking, it goes through all the objects in the universe and collects those with a T. More exactly, it is the set of all objects in U that are assigned T by the open statement p(x).
For example, {x in N9 | 3 < x < 8} = the set of all objects in N9 that are between 3 and 8 = {4,5,6,7}.
The idea of truth sets reveals an intimite connection between sets and open statements. According to [1.4] every open statement has a (unique) truth set. Conversely for any set S in the universe there is an open statement x is in S whose truth set is S. It is called the trivial open statement for S. There are other open statements with that same universe and with that same truth set.
[1.6] (Relationship between sets and open statements)
(a) Every open statement determines a subset of its universe, namely its truth set.
(b) For every subset of a universe there is an open statement whose truth set equals that subset, namely the trivial open statement.
Often in the same discussion there are more than one open statement all with the same universe. Each independently assigns truth values to all the objects in that universe. If there are two open statements then each object receives two truth values.
For any set S in a universe U there are many open sets p(x), q(x), r(x), ... whose truth sets equal S. For example:
x > 3 and x < 8, x + 1 is between 4 and 9, x is between the roots of x2 - 11x + 24, x is in {4,5,6,7}
where S = {4,5,6,7}. However, all such open statements must be equivalent to each other, and therefore, equivalent to the trivial open statement x is in S.
[1.7] (Equivalent open statements) Open statements with the same universe are equivalent if and only if they all have the same truth set.
The argument supporting [1.7] is simple.
If the open statements are equivalent, then each object in the universe receives equal truth values from the open statements. Therefore, the objects receiving a T from one open statement must also receive a T from all the other open statements. So their truth sets must be the same.
Conversely, suppose the open statements have the same truth set. Then all open statements assign a T to every object in the truth set and an F to every object not in the truth set. Therefore, equal truth values assigned to all objects in the universe. By [1.5] the open statements are equivalent.
Examples:
The equations x + 1 = 5 and x + 2 = 6 with universe N are equivalent because they have the solution set {4}.
If both sides of an equation are multiplied by the same natural number then an equivalent equation is obtained.
-----
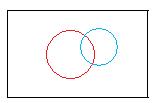 In the following sections there are discussions involving more than one open statement, all with the same universe. Two open statements will assign two truth values to each object and determine two subsets (truth sets) in that universe, three open statements - three truth values to each object and three subsets (truth seets) in that universe, etc. The assignments of truth values to objects are done independently. Sometimes colors will be used to coordinate names, open sets and geometric models. The adjacent figure is the geometric model of the truth sets S1, S2 of two unspecified open statements p(x), q(x) . Depending on the positions of the circles, these open statements may assign any of the following pairs of truth values to each object in the universe:
In the following sections there are discussions involving more than one open statement, all with the same universe. Two open statements will assign two truth values to each object and determine two subsets (truth sets) in that universe, three open statements - three truth values to each object and three subsets (truth seets) in that universe, etc. The assignments of truth values to objects are done independently. Sometimes colors will be used to coordinate names, open sets and geometric models. The adjacent figure is the geometric model of the truth sets S1, S2 of two unspecified open statements p(x), q(x) . Depending on the positions of the circles, these open statements may assign any of the following pairs of truth values to each object in the universe:
(#)
TT,
TF,
FT,
FF
Here is a numerical example of two specific open statements:
Let the universe be N9, and p(x),
q(x) be open statements with that universe, and defined by
p(x): 3 < x, q(x): x < 8
Then from the pairs
p(1)q(1),
p(2)q(2),
p(3)q(3),
p(4)q(4),
p(5)q(5),
p(6)q(6),
p(7)q(7),
p(8)q(8),
p(9)q(9)
each object in the universe receives two truth values:
1 FT
2 FT
3 FT
4 TT
5 TT
6 TT
7 TT
8 TF
9 TF
Notice that no object in this example receives the pair FF. As will be seen later, such an omission means that some relation exists between the open statements, and also between their truth sets.
[1.8] (Logically unrelated open sets) Two open statements with the same universe are unrelated if together their assignments of truth values to all the objects in the universe involves all four pairs of truth values in (#).
Notation:
In the universe, unrelated open sets p(x), q(x)
assign TT to some object,
assign TF to another object,
assign FT to another object,
assign FF to another object.
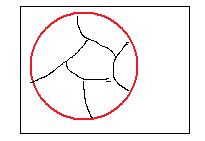
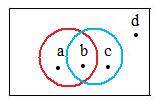 The adjacent figure shows the truth sets of two unrelated open sets. The trivial open statements involving point x
The adjacent figure shows the truth sets of two unrelated open sets. The trivial open statements involving point x
x is inside the red circle,
x is inside the blue circle
assign the following pairs of truth values to the four points a, b, c, d:
b TT
a TF
c FT
d FF
The pairs of truth values assigned to these four points are enough to show that the open statements are unrelated.
What two pairs of truth values are never assigned by equivalent open statements?
Section 2: Some operations on sets: intersection, union and complement
In this section certain operations will be discussed. Intuitively speaking, they create "new"sets from sets already existing in the same universe. Special symbols denote these operations. A figure serves as a visible geometric model and subsets of N9 often accompany the discussion of each operation. Intuitive arguments usually motivated by the examples give support for some statements made in this section. More substantial arguments and proofs are given in Section 4.
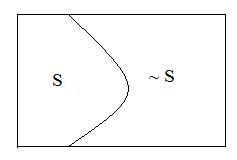 Let S be any set in a universe U. Collect all objects in U but outside of S to form a new set ~S. In the adjacent figure, if S is the set of all points in the left part of the figure, then ~S is the set of all points in the right part.
Let S be any set in a universe U. Collect all objects in U but outside of S to form a new set ~S. In the adjacent figure, if S is the set of all points in the left part of the figure, then ~S is the set of all points in the right part.
[2.1] (Complement) The complement of a given set in a universe is the collection of all objects (in the universe) that are not in the given set.
Notation1: In a universe U, x is in ~S if and only if x is not in S.
Notation2: ~S = {x in U | x is not in S}.
Notation3: In U, if S is a truth set then all objects in ~S have been assigned an F.
Notation4: Let p(x) be an open statement with universe U. If p(x) assigns a truth value to any object in U, then the negative ~p(x) assigns the opposite truth value to that same object. (The subset of U determined by ~p(x) is the complement of the subset determined by p(x).)
Another notation for complement is U\S (a special form of set subtraction defined in [2.12] below). This notation indicates the need for knowing the universe U as well as S in order to determine the complement of S.
Example: in the universe N9 = {1,2,3,4,5,6,7,8,9
}
let S = {1,3,5,7,9}. Then the complement of S is ~S = {2,4,6,8}.
If a tilda (~) is "attached" to a set symbol S then the complement ~S of that set is formed. Therefore the tilda (~) is a unary operation on individual sets. Its attachment to the name of a given set denotes the results of the operation, namely, the creation of a single set which is the complement of the given set.
It is obvious that the complement of ~S must be S, because S contains all objects in the universe not in ~S. Therefore, the complement of the complement of a set is the set itself. ~ ~S = S. This also means that ~~p(x), p(x) have the same truth set, and hence are equivalent. The operation of the tilda resembles the operation of negation in algebra: the negative of a negative of number w = -(-w) = w. (Later such operations will be called involutions.)
Example: In the previous example S = {1,3,5,7,9}.
Then ~~S = ~(~S) = ~{2,4,6,8} = {1,3,5,7,9} = S.
The negative of the negative of an open statement is logically equivalent to the open statement itself.
Let p(x) be some open statement with universe U. Let b be any object in that universe.
If p(b) = T then ~p(b) = F. Hence ~~p(b) = T.
If p(b) = F then ~p(b) = T. Hence ~~p(b) = F.
Since b is any object in U, it can be said that p(x) and ~~p(x) assign the same truth value to each object in U. Therefore, p(x), ~~p(x) are equivalent open statements.
If p(x): x is in S, then ~p(x): x is not in S, and then ~~p(x): x is back in S.
It was mentioned in the previous section that the empty set Φ is a subset of any universe U. Therefore, every object is not in Φ and therefore must be in ~Φ. The complement of the empty set is the entire universe.: ~Φ = U\Φ = U. Similarly, the complement of the universe is the empty set: ~U = U\U = Φ. Hence, every subset in a universe has a complement in that same universe
-----
Whereas a unary operation accepts only one thing (and produces a second thing) a binary operation accepts two things and produces a third thing. For example, the arithmetic operation of addition accepts 3 and 5 and produces 8. The operation of multiplication accepts 3 and 5 and produces 15. In the case of sets, each operation on sets accepts two given sets, often designated as S1, S2, and produces a single set from them, all in the same universe. At the same time there are two open sets whose truth sets are the given sets. In any case, there exist the two trivial open statements
x is in S1,
x is in S2
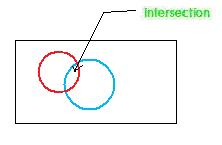
The intersection of streets is that portion common to both streets.The adjacent figure shows the intersection of the interiors of a circle and another circle.
[2.2] (Intersection) The intersection of two sets in the same universe consists of all objects that are in both sets.
Notation1: S1 /\ S2 = {x in U | x is in S1 and x is in S2}.
Notation2: x is in S1 /\ S2 if and only if x is in S1 and x is in S2 (a true statement about universally true equivalence)
Notation3: In U, if S1 is a truth set and S2 is a truth set then all objects in S1 /\ S2 are assigned TT.
The common notation for intersection is an upside down U:
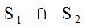
But for typographical reasons, the notation /\ will be used in all volumes to denote intersection.
Example: In N9 the intersection {2,3,4,5,6} /\ {4,5,6,7,8} = {4,5,6}.
Simply go through the two sets {2,3,4,5,6}, {4,5,6,7,8} and select those numbers in both sets:
{2,3,4,5,6}, {4,5,6,7,8}.
For a determination of the truth set of a conjunction of open statements click here.
From the wording of definition [2.2] it is obvious that the intersection of two sets is the same no matter which set is written first.
[2.3] (Commutativity) The operation of intersection is commutative.
Notation: S1 /\ S2 = S2 /\ S1.
But what happens to the intersection if one or both sets are empty? For example, what is the intersection {2,3,4,5,6} /\ Φ? The open statements
x is in {2,3,4,5,6}, x is in Φ
make the following assignments of truth values:
1 FF,
2 TF,
3 TF,
4 TF,
5 TF,
6 TF,
7 FF,
8 FF,
9 FF
No number in N9 is assigned TT. Therefore, no number is in the intersection. This means
{2,3,4,5,6} /\ Φ = Φ
In general, if either of two sets is empty then their intersection is empty: S /\ Φ = Φ,
Φ /\ S = Φ, Φ /\ Φ = Φ
By definition, the open statement x is in Φ is universally false. Therefore, any conjunction involving that phrase will have to be universally false.
The intersection of any set and the universe is equal to that set:. S /\ U = S, U /\ S = U, U /\ U = U
Click here to see the an argument supporting this statement.
These last statements about intersection are similar to statements about numbers and multiplication:
0n = 0, n0 = 0, (0)(0) = 0, 1n = n, n1 = n, (1)(1) = 1.
The intersection of more than two sets is defined in the obvious way:
[2.4] The intersection of sets in the same universe consists of all objects that are in all the given sets
Notation: x is in S1 /\ S2 /\ S3 /\ ... if and only if x is in S1 and x is in S2 and x is in S3 and ...
Parentheses surround an operation to be done first. Short arguments can be made to support the two equalities
(S1 /\ S2) /\ S3 = S1 /\ S2 /\ S3,
and
S1 /\ (S2 /\ S3) = S1 /\ S2 /\ S3
Therefore,
[2.5] (Associativity) The operation of intersection is associative.
Notation: (S1 /\ S2) /\ S3 = S1 /\ (S2 /\ S3).
---------
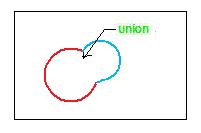
The adjacent figure shows the union of a set and another set. It is the combined interiors of the two sets, including their intersection if they overlap.
[2.6] (union) (In the same universe) the union of two sets is the collection of all objects in either set (or both)
Notation1: S1 \/ S2 = {x in U | x is in S1 or x is in S2}.
Notation2: x is in S1 \/ S2 if and only if x is in S1 or x is in S2 (a true statement about universally true equivalence)
Notation3: In U, if S1 is a truth set and S2 is a truth set then all objects in S1 \/ S2 are all objects not assigned FF.
The common notation for union is a U:
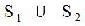
But for typographical reasons, the notation \/ will be used in all volumes to denote union.
Example: In N9 the union {2,3,4,5,6} \/ {4,5,6,7,8} = {2,3,4,5,6,7,8}.
Simply go through the two sets {2,3,4,5,6}, {4,5,6,7,8} and select those numbers in either set, but nothing outside both sets.
From the notation following [2.6] it obvious that that an alternation of open statements determines the union of sets. And in doing so, it shows how a union assigns truth values to each object in the universe. For a determination of the truth set of an alternation of open statements click here.
Notation3 of [2.6] provides a negative definition of a union of two sets. The following is actually equivalent to [2.6] (see [5.6c] in Volume A, chapter 1):
[2.7] (Negative definition a union) In a universe the objects outside a union of sets are exactly those outside every set.
Notation1: x is not in (S1 \/ S2) if and only if x is not in S1 and x is not in S2.
Notation2: ~(S1 \/ S2) = ~S1 /\ ~S1.
(Complement of a union of two sets in a common universe is equal to the intersection of their complements.)
Notation3 (De Morgan's law): ~(p(x) or q(x)) <==> ~p(x) and ~q(x)
-----
Click here for a discussion of duality between intersection and union.
The duality of notation 3 above is also called De Morgan's law:
~(p(x) and q(x) <==> ~p(x) or ~q(x).
[2.8] (Commutativity) The operation of union is commutative.
Notation: S1 \/ S2 = S2 \/ S1.
-----
But what is the union {2,3,4,5,6} \/ Φ involving the empty set? The open statements
x is in {2,3,4,5,6}, x is in Φ
make the following assignments of truth values:
1 FF,
2 TF,
3 TF,
4 TF,
5 TF,
6 TF,
7 FF,
8 FF,
9 FF
No number in N9 is assigned FF. Therefore, no number is excluded from the union. this means
{2,3,4,5,6} \/ Φ = U
This suggests that the union of any set and the empty set is that set.. S \/ Φ = S (Click here to see an indirect proof of this statement.)
The union of any set and the universe is equal to the universe. S \/ U = U
The proof of this is very similar to that for the union with the empty set. Click here to see the proof.
If 1 represents the universe U and 0 represents Φ then the representations of the four intersections of these two sets produce a strange (Boolean) addition table for 1 and 0. Click here to see this discussion.
The union of more than two sets is defined in the obvious way.
[2.9] The union of sets in the same universe consists of all objects that are in any of the sets
Notation: x is in (S1 \/ S2 \/ S3 \/ ...) if and only if x is in S1 or x is in S2 or x is in S3 or ...
It is sometimeds useful to discuss objects not in the union of two sets. It is a form of De Morgan's law.
[2.10] (Outside a union of sets) An object is not in a union of sets all in the same universe if and only if that object is in none of the sets.
Notation:
x is not in S1 \/ S2 \/ S3 \/ ... if and only if
all the open statements x is in x is in S1 or x is in S2 or x is in S3 or ...
Short arguments can be made to support the two equalities
(S1 \/ S2) \/ S3 = S1 \/ S2 \/ S3,
and
S1 \/ (S2 \/ S3) = S1 \/ S2 \/ S3
Therefore,
[2.11] (Associativity) The operation of union is associative.
Notation: (S1 \/ S2) \/ S3 = S1 \/ (S2 \/ S3).
------
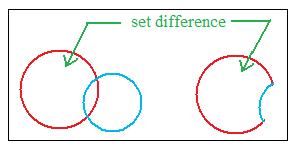 Occasionally useful is a type of subtraction of sets. Intuitively speaking, the subtraction of a second set set from a first set removes some of the objects in the first set.
Occasionally useful is a type of subtraction of sets. Intuitively speaking, the subtraction of a second set set from a first set removes some of the objects in the first set.
[2.12] (Set difference) The result of a set subtraction of a second set from a first set is the collection of all objects in the first set that is not in the second set. The result is often called the set difference.
Notation: x is in (S1\ S2) if and only if x is in S1 and x is not in S2.
Intuitively speaking, the second set takes away objects from the first set. Also, it is the remaining part of the first set after the intersection of the two sets is removed.
Example: Let N9 be the universe.
{2,3,4,5,6}\{4,5,6,7,8} = {2,3}
The numbers 1,7,8,9 play no role in determining this difference {2,3} of sets. Intuitively speaking, the numbers 4,5,6 are removed from the set {2,3,4,5,6}. But {4,5,6} is the intersection of the two sets. This suggests that the set difference can be obtained by removing the intersection of two sets from the first set:
S1\S2 = S1\(S1 /\ S2)
The set difference {3,5,7}\{3,4,5,6,7} = Φ because 3,5,7 are removed from the first set {3,5,7}. The objects 4 and 6 have no effect on the operation.
Let S be a any set in a universe U.
As expected, S\Φ = S because nothing is taken away from S.
But S\S = Φ because everything is taken away from S.
And for the same reason, S\U = Φ
Section 3: Some relationships between two sets in the same universe
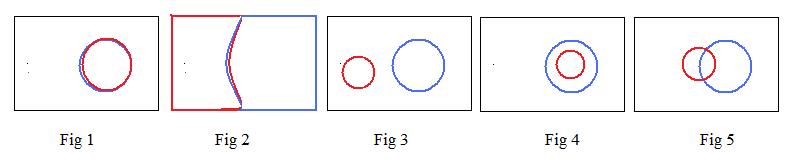
In the geometric model the interior of a rectangle is the universe and sets are the interiors of closed curves, usually circles, inside the rectangle. In each of the rectangles in the following figures, except for Fig 2, there are two sets S1 and S2 that are the interiors of red and blue circles.
 Statements may be made about relationships between the circles. The statements may be true or false. Therefore, they are logical statements.
Statements may be made about relationships between the circles. The statements may be true or false. Therefore, they are logical statements.
In Fig 4, S1 is completely inside S2.
In Fig 1, S1 and S2 coincide.
But it can still be said that S1 is completely inside S2
In Fig 3, S1 and S2 are completely separated.
These expressions "is completely inside", "coincide" and "are completely separated" state relationships between the sets. All three relationships just given are true. However, the following statement
In Fig 5, S1 is completely inside S2
is obviously false.
Part of S1 lies outside of S2. In that part are points inside S1. And those same points are not in S2.
Any object in the universe that makes a relation between sets false is called a counterexample to the relation.
Sets are determined by the objects in them. The sets S1 and S2 are truth sets of the trivial open statements
(&&)
x is in S1,
x is in S2
They assign a pair of truth values to each object in the universe. All pairs are selected from
TT,
TF,
FT,
FF.
A relation between sets determines what pair of truth values is assigned to each object in a universe.
-----
The most simple relationship is equality. In Fig 1 the two sets coincide: S1 = S2. As a result, points inside them are assigned TT by (&&). All other points are outside the interiors and are assigned FF. So (&&) assigns a pair of equal truth values to every object in the universe.
[3.1] (Equality of sets) Two sets in the same universe are equal if and only if they contain exactly the same elements.
Notation 1: S1 = S2 if and only if the open statements x is in S1, x is in S2 assign equal truth values to each object in the universe.
Notation 2: S1 = S2 if and only if the equivalence x is in S1 <==> x is in S2 is universally true.
Example: In universe N9, {5,7,6,8,4} = {4,5,6,7,8} because they contain exactly the same numbers. Any number in N9 is in both of them (is assigned TT) or it is in neither of them (is assigned FF). But notice that this shows the listing of the objects in a set can be written in different arrangements of the same objects (permutations).
Click here to see a discussion supporting the fact that all empty sets are equal. In other words, in any universe there is only one empty set. It is unique.
---------
For equality (&&) assignes equal truth values to each object in the universe. The other extreme is that (&&) assigns opposite truth values.
But this means that each set is the complement of the other.
[3.2] (Complementary sets) Two sets inside the same universe are complementary if and only if one is the complement of the other.
In Fig 2, S2 contains everything not in S1 and conversely. Every object in the universe is assigned a pair of opposite truth values: TF or FT from the open sets in (&&).
Example: Inside the universe N9 the two sets {1,3,5,7,9} and {2,4,6,8} are complementary.
[3.3] Two sets in the same universe are complementary if and only they satisfy both both of the following conditions:
(a) their union is the universe;
(b) their intersection is empty.
Notice that {1,3,5,7,9} /\ {2,4,6,8} = Φ and that {1,3,5,7,9} \/ {2,4,6,8} = N9, the universe.
Click here for a discussion supporting [3.3].
------
Relax condition (a) in [3.3] to get a more general situation as shown in Fig 3. The two sets do not overlap. There is nothing in their intersection. No point in the universe can be assigned TT by the open statements (&&). However if their union is not the entire universe then some objects outside the union will be assigned FF.
[3.4] (Disjoint sets) In the same universe a pair of sets are disjoint if and only if their intersection is empty
Notation: S1, S2 are disjoint if and only if the open statements
x is in S1, x is in S2
are incompatible (no object in the universe is assigned TT by the trivial open statements above).
A pair of complementary sets are always disjoint, but not conversely. Fig 3 shows disjoint sets that are not complementary.
Notice that in definition [3.4] the word "object" is not used. The definition is made at a higher level using only "sets."
-------
Fig 4 shows an important situation: all of one set may be part of another set.
This means that all the points in first set are also in the second set.
[3.5] (Inclusion) One set is included in a second set if and only if every object in the first set is also in the second set.
Notation: S1 < S2 if and only if x is in S1 => x is in S2.
If one set is included in a second set then the first set is called a subset of the second set. Obviously, every set in a universe is a subset of that universe.
Example:
Let the universe N9 = {1,2,3,4,5,6,7,8,9}. It is obvious that {4,5,6} is included in {3,4,5,6,7,8}.
Also the implication if x is in {4,5,6} then x is in {3,4,5,6,7,8} is obviously .true.
If two sets are equal then the content of either set is included in the other. If one set is equal to a second set then the first set is included in the second set. The underline in the notation < allows inclusion to extend to equality:
S1 < S2
means
S1 < S2 or S1 = S2
read "weak inclusion means strict inclusion or equality."
The reverse of inclusion is containment.
A set S2 contains a set S1 if and only if S1 is included in S2
Notation: S2 > S1
If one set contains another then the first set is sometimes called a superset of the second set.
If S1 = S2 then trivially everything in S1 is in S2. Therefore every set is included it itself. It is a subset of itself.
The symbol < is used in these discussions to mean inclusion but not equality. It is called strict inclusion. The statement
S1 < S2
is true for the sets in Fig 4 but not true for the sets in Fig 1. The first set is called a proper subset of the second set.
In contrast, the symbol < allows both strict inclusion and equality. (It is sometimes called a weak inclusion.) Therefore, the statement
S1 < S2
is true for both Fig 4 and Fig 1.
There is also strict containment, S2 > S1. In this situation S2 contains all of the objects in S1 plus one or more objects not in S1. The statement
S2 > S1
is true for FIg 4 but not true for Fig 1.
Section 4: More on inclusion, implication and proof
The inclusion of one set in another is a simple idea. That simplicity can be used to an advantage in discussions of implications involving open statements.
The following three figures will be needed in this section:
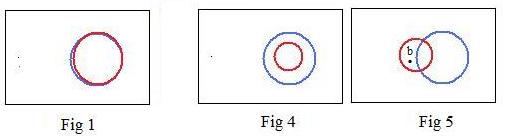 S1, S2 continue to denote the interiors of the red and blue circles.
S1, S2 continue to denote the interiors of the red and blue circles.
Also used are the trivial open statements
(&&)
x is in S1,
x is in S2
which assign a pair of truth values to each point in the universe.
In Fig 4 and Fig 1, set S1 is entirely inside set S2. But in Fig 5, set S1 is not entirely inside set S2. Part of S1 lies outside of S2. There are points in that part. Any of those points is called a counterexample to the inclusion S1 < S2. If point b is one of those counterexamples, then (&&) assigns truth values TF to point b. That point b is also a counterexample to (the universality of) the implication
x is in S1 ==> x is in S2
because b produces a false component
b is in S1 --> b is in S2
(true hypothesis, false conclusion).
The following negative statement is equivalent to definition [3.5]. It is seemingly trivial, yet is sometimes useful as a basis for arguments supporting inclusions and universally true implications of open statements.
[4.1] (Inclusion) One set is included in another if and only if there are no counterexamples to this inclusion.
Notation1: S1 < S2 if and only if there exists no object b such that b is in S1 and b is not in S2.
Notation2: S1 < S2 if and only if no object in the universe is assigned TF by the open statements (&&) respectively.
Example: Again let the universe be N9 = {1,2,3,4,5,6,7,8,9}.
A counterexample to {1,2,3,4} < {3,4,5,6,7,8} is 1. So is 2. Each is in {1,2,3,4} but not in {3,4,5,6,7,8}. The remaining numbers 5,6,7,8,9 in U do not qualify as counterexamples, because none of them are in {1,2,3,4}. Therefore, they cannot produce false components. The statement about inclusion {1,2,3,4} < {3,4,5,6,7,8} is false because there are counterexamples.
The following statement provides a useful method to prove two sets are equal.
[4.2] (Equality from reverse inclusions) If two sets are included in each other then the two sets are equal.
Notation1: if S1 < S2 and S2 < S1 then S1 = S2
Notation2: if p(x) ==> q(x) and q(x) ==> p(x) then p(x), q(x) are equivalent.
The inclusions if S1 < S2 and S2 < S1 prevent any object from being assigned TF or FT. Therefore every object is assigned equal truth values, TT or FF, which is what happens only with equal sets and their trivial equivalent open statements.
The implication q(x) ==> p(x) is called the converse of the implication p(x) ==> q(x). The converse of a (universally) true implication may or may not be (universally) true. For example, in universe N9 the implication
x <5 ==> x < 8
is universally true, but its converse
x < 8 ==> x < 5
has a counterexample, namely 7. Upon substitution for x, 7 makes the hypothesis x < 8 true, but the conclusion x < 5 false.
Statement [4.1] can be used to prove that the empty set Φ is a subset of any set S in any universe U:
Φ < S.
The basic argument is that it is impossible to find a counterexample to this inclusion. Suppose there is a counterexample b. Then by definition b is in Φ and b is not in S. But there is no b in Φ because, by definition, Φ is empty. So no counterexample b can exist.
This argument uses a typical approach for denying the existance of a counterexample: assume that there is a counterexample and then arrive at an impossible situation because of that assumption. Such an argument is called an indirect argument.
Both the empty set and the set itself are called the trivial subsets of the set itself. Often they are less interesting than the other subsets called proper subsets.
It is true that 2 < 5. But it is also true that -5 < -2. Negation of numbers interchanges the sides of an inequality. (This can be proven by subtraction of the smaller number from the larger.)
It is obvious that if a first set is included in a second set, then objects outside of the second set must also be outside the first set. But being outside a set is the same as being in the complement of that set. Let the two sets be A and B. Then
if A < B then ~B < ~A
Therefore the operation of complementing interchanges the sides of an inclusion.
Now let B and A equal the complements of S1 and S2 respectively. The implication becomes
if ~S2 < ~S1 then S1 < S2
(Recall that the complement of a complement is the original set: ~~S = S.) This statement provides another method for proving the inclusion of one set in another:
[4.3] (Inclusion from complements) A first set is included in a second set if the complement of a second set is included in the complement of the first.
Notation1: if ~S2 < ~S1 then S1 < S2.
Notation2: if ~q(x) ==> ~p(x) then p(x) ==> q(x).
The implication ~q(x) ==> ~p(x) is called the contrapositive of the implication p(x) ==> q(x). It can be proven that an implication and its contrapositive always have the same truth value. Consider the implications
if person x is in Washington then person x is in the USA. if person x is not in the USA then person x is not in Washington
Both implications are universally true. The second implication might be used by a traveller needing an alibi.
In many situations it is possible to combine two inclusions into a single inclusion. It presupposes all sets and open statements have the same universe. (A long telescope can be compressed into a smaller, compact device that is easier to transport.)
[4.4] (Telescoping property of two inclusions) In any universe, if a first set is included in a second set, and the second set is included in a third set, then the first set is included in the third set.
Notation1: if S1 < S2 and S2 < S3 then S1 < S3.
Notation2: if x is in S1 ==> x is in S2 and x is in S2 ==> x is in S3 then x is in S1 ==> x is in S3.
Notation3: for any open statements p(x), q(x), r(x) with a common universe, if the implications p(x) ==> q(x) and q(x) ==> r(x) are both universally true, then the implication p(x) ==> r(x) is universally true.
In notation2 there are three implications involved:
(1) x is in S1 ==> x is in S2,
(2) x is in S2 ==> x is in S3,
(3) x is in S1 ==> x is in S3,
Implications (1) and (2) are given as universally true. Then neither has any counterexamples. Now begins the argument that (3) has no counterexamples. Suppose there is a counterexample b. This means that b is in S1, but not in S3. Since (1) has no counterexamples, then b is also in S2. Since (2) has no counterexamples, b is in S3. But this prevents b from being a counterexample to (3). So (3) can have no counterexamples.
In notation3 let S1, S2, S3 be the truth sets of p(x), q(x), r(x) respectively. Then the three implications
p(x) ==> q(x), q(x) ==> r(x), p(x) ==> r(x)
are equivalent to implications (1), (2), (3) respectively.
There is an obvious extension of [4.4] to more than two inclusions. It is discussed in the next section. (But see [5.3] there.)
Section 5: Families of sets
A set is a collection of objects. The objects are allowed to be abstract as well as tangible. This means that the objects themselves could be sets. The term "a set of sets" is confusing. Instead a family of sets will be used. Intuitively speaking this means there are three levels of collections: basic objects, sets of objects, and families of sets. In this section there will be no need to discuss collections of families, a still higher level.
In most indcussions families will have only a finite number of sets in them.
The following is an example:
In the universe N9 the following are subsets of this universe:
S1 = {1,5,6}, S2 = {2,7,8,9}, S3 = {3,4,5,6}, S4 = {1,3,5,7,9}
Collect these four subsets without changing their contents into a family of four sets:
{S1, S2, S3, S4}
This family has all the properties of a set. However there is no standard way of writing the name of a family of sets. In discussions here, the name will be an underlined capital letter:
W = {S1, S2, S3, S4}
to avoid any confusion when necessary. It is meaningful (and true) to say that S1 is a set in W or simply, S2 is in W. If S = {3,6,9} then S is not in W. Not in W are any of the sumbers 1,2,3,4,5,6,7,8,9 themselves because the family consists of subsets, not numbers. To avoid paradoxes, V cannot be a set in V:
V = {S1, S2, S3, S4, V} is not permitted
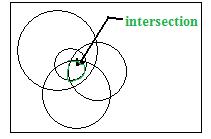
 A restriction on families of sets is: No family can be a set in that family. There are more restrictions but families in discussions here will be simple enough not to violate any of the rules. And in discussions here most sets in a family will be in a common university. The adjacent figure shows a random collection of circles whose interiors form a family.
A restriction on families of sets is: No family can be a set in that family. There are more restrictions but families in discussions here will be simple enough not to violate any of the rules. And in discussions here most sets in a family will be in a common university. The adjacent figure shows a random collection of circles whose interiors form a family.
Since the empty set Φ and the universe U are genuine subsets of U, then Φ and U may be members of some families of subsets of U.
In the universe of the plane in plane geometry, straight lines are special sets of points. Therefore, any collection of straight lines is a family of sets. The family of all straight lines is a example of an infinite family of sets. The familiar properties of straight lines can be restated as properties of this family. Click here for more discussion of this geometric family of straight lines.
-----
For any given set, there is a unique family of all subsets of that set. For example, all the subsets of S={1,3,5} are
Φ, {1}, {3}, {5}, {1,3}, {1,5}, {3,5}, {1,3,5}
That family is called the power set of the given set.
There is a notation for the power set P(S) of S. .
If S={1,3,5} then
P(S) = the power set of S = {Φ, {1], {3}, {5}, {1,3}, {1,5}, {3,5}, {1,3,5}}
Also Q(S), R(S) may denote power sets of S.
The following statement provides a method that helps in checking if all the subsets have been displayed:
[5.1] (Size of the power set) If a set has n objects then its power set has 2n subsets in it.
Examples: There are 23 = 8 subsets of {1,2,3}. There are 29 = 512 subsets of the set N9.
A discussion supporting [5.1] will be given in a later volume. The attempt to extend this statement to the power set of infinite sets like N leads to an interesting concept of transfinite numbers and their strange arithmetic.
Let the reader show that [5.1] is true even when the given set is the empty set Φ.
-----
If S1, S2, ..., Sn are n subsets of a common universe U, then they form a finite family of subsets of U:
(*) { S1, S2, ..., Sn}
Here n is any natural number in N. In previous sections, most discussions involved just two subsets (n=2). From them intersections and unions were formed. Also pairs of subsets were compared. It is obvious that many of these operations and comparisons can be extended to sets in a family. There are corresponding extensions to open statements:
(**)
p1(x), p2(x), ... pn(x)
The trivial open statements
p1(x): x is in S1, p2(x): x is in S2, ..., pn(x): x is in Sn
relate the open statements and the corresponding subsets in the family of subsets above.
This may be called a family of corresponding open statements.
[5.2] (Generalizations) The following are generalizations of statements in previous sections about two or three sets.
 [a] The intersection S1 /\ S2 /\ ... /\ Sn consists of all objects in that are in every subset (*).
[a] The intersection S1 /\ S2 /\ ... /\ Sn consists of all objects in that are in every subset (*).
x is in (S1 /\ S2 /\ ... /\ Sn) if and only if
(x is in S1) and (x is in S2) and ... and (x is in Sn)
The conjunction p1(x) and p2(x) and ... and pn(x) assigns a T to an object in U if and only if
every open statement (**) assigns a T to that same object.
 [b] The union S1 \/ S2 \/ ... \/ Sn consists of all objects in that are in one or more subsets (*).
[b] The union S1 \/ S2 \/ ... \/ Sn consists of all objects in that are in one or more subsets (*).
x is in ( S1 \/ S2 \/ ... \/ Sn) if and only if
(x is in S1) or (x is in S2) or ... or (x is in Sn)
The alternation p1(x) or p2(x) or and ... or pn(x) assigns a T to an object in U if and only if
one or more open statement (**) assign a T to that same object.
 [c] A family of sets covers a given set if and only if the given set is included in the union of all sets in the family.
[c] A family of sets covers a given set if and only if the given set is included in the union of all sets in the family.
The family (*) covers set S if and only if S is included in the union S1 \/ S2 \/ ... \/ Sn.
(**) covers S if and only if x is in S implies x is in S1 or x is in S2 or ... or x is in Sn.
Example: In N9 if S={4,5,9} and S1={1,2}, S2={4,5,6}, S3={8,9} then {S1, S2, S3} covers S
because S is included in S1 \/ S2 \/ S3 = {1,2,4,5,6,8,9}.
 [d] A family of sets is disjoint if and only every pair of sets in the family is disjoint.
[d] A family of sets is disjoint if and only every pair of sets in the family is disjoint.
The family (*) is disjoint if and only if for every distinct i,j, Si /\ Sj = Φ
Example1: In N9 if S1={1,3,5}, S2={2}, S3={6,8}, S4={4}, then {S1, S2, S3, S4} is a family of disjoint sets.
Example2: A family of parallel lines is disjoint.
 [e] A family of subsets of a given set is a partition of a given set if and only if the family is disjoint and covers the given set.
[e] A family of subsets of a given set is a partition of a given set if and only if the family is disjoint and covers the given set.
In other words, a family of sets is a partition of a given set if and only if the family satisfies three conditions:
(i) every set in the family is included in the given sett;
(ii) The family is a disjoint family;
(iii) The family covers the given set.
 [f] A family of sets is an increasing chain of sets if each set is included in the next set (except for the last set).
[f] A family of sets is an increasing chain of sets if each set is included in the next set (except for the last set).
Notation: The family {S1, S2, ..., Sn} is an increasing chain of sets if and only if
S1 < S2 and
S2 < S3 and
S3 < S4 and
... and
Sn-1 < Sn
Often the conjunctions are omitted:
Increasing chain: S1 < S2 < S3 < ... < Sn
Strictly increasing chain: S1 < S2 < S3 < ... < Sn
Decreasing chain: S1 > S2 > S3 > ... > Sn
Strictly decreasing chain: S1 > S2 > S3 > ... > Sn
If all the inclusions and containments are true, then the chains telescope into single relations:
S1 < Sn, S1 < Sn,
S1 > Sn, S1 > Sn.
-----
Consider blankets on a very large bed. to cover the entire bed it may require several blankets that may overlap. The bed is under the combined collection of blankets. A similar situation may exist for some given set in a universe. A set may be "covered" by other sets in that universe.
Notice that W does not cover the whole universe N9, because 3 and 7 are not in any of the sets in W.
Also the set {1,2} is in W, but it does not even intersect S. In an intuitive sense, {1,2} is not essential to the covering. (But it still is a member of the covering.)
It is quite possible that all the sets in a covering be disjoint. Then the family is called a disjoint covering of the set. The disjoint covering is a special family of sets. Intuitively speaking, the set is broken down into pieces which are subsets in the family.
[5.4] (Partitions) A partition of a set is a disjoint covering of the set by its own subsets.
In other words, a partition separates the entire given set into a family of disjoint subsets. The union of all those subsets is the given set. In the universe N9 an example of a partition of S = {2,3,4,5,6,7,8} is the family
{ {2,8}, {3.4}, {5,6,7} }
More partitions of S are the families:
{ {2,3,4,5}, {6,7,8} }
{ {2}, {3}, {4}, {5}, {6}, {7}, {8} }
{ {2,3,4,5,6,7,8} }
of three, seven and one subsets of S respectively.
The sets in the family { {2,8} {3.4} {5,6,7}, {1,9} } are disjoint, but the family is not a partition of S = {2,3,4,5,6,7,8} because {1,9} is not a subset of S. The family is only a disjoint covering of S.

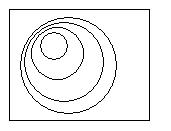
The adjacent figure shows a partition of the interior of a circle into colored subsets (sub-arias).
Sometimes it is useful to partition a large set into a family of smaller subsets which can be more easily measured. Nothing is lost during the partitioning process. For example, suppose a large number of coins in a pile are to be counted. Partition the coins into several smaller piles. Have each of the smaller piles counted by different people. Add together the number of coins in each smaller pile.
Suppose family
W = {S1, S2, S3, .... Sn}
where S1, S2, S3, .... Sn are n subsets of of the same universe.
Then W is a linear family of increasing sets if each set is included in the next set:
S1 < S2, S2 < S3, S3 < S4, ..., Sn-1 < Sn
This is often shortened and written as a chain of inclusions:
S1 < S2 < S3 < S4 < ... < Sn
Similarly, W is a linear family of decreasing sets if each set contains the next set:
S1 > S2, S2 > S3, S3 > S4, ..., Sn-1 > Sn
These may also be written as a chain of containments.
A linear family of sets is either a linear family of increasing sets or a linear family of decreasing sets.
Example: if
S1={1}, S2={1,5}, S3={1,2,3,5,7}, S4={1,2,3,4,5,7,8},S5={1,2,3,4,5,6,7,8}
then {S1, S2, S3, S4, S5} is a linear family of increasing sets. There is a a chain
S1 < S2 < S3 < S4 < S5
Similarly, {S5, S4, S3, S2, S1} is a linear family of decreasing sets.
It is customary to list the sets in these families in the order of inclusion or containment.
Let p1(x) be any open statement equivalent to x is in S1;
Let p2(x): be any open statement equivalent to x is in S2;
Let p3(x): be any open statement equivalent to x is in S3;
.............................................................................................................
Let pn(x): be any open statement equivalent to x is in Sn.
Then the chain of n included sets induces the chain
p1(x) ==> p2(x) ==> p3(x) ==> ... ==> pn(x)
of implications.
[5.5] (Telescoping sets) For a family of n increasing sets, the first set is included in the last set.
Notation1: if S1 < S2 < S3 < S4 < ... < Sn
then S1 < Sn.
Notation2: if p1(x) ==> p2(x) ==> p3(x) ==> ... ==> pn(x) then p1(x) ==> pn(x).
A discussion supporting this statement will be given later after a discussion of positive integers, in particular mathematical induction. But it is pattered after the supporting statements for [4.4].
 Usually all objects involved in a discussion form a collection called a universe. Objects outside a universe are ignored. Aninterior of a rectangle may serve as an example of a universe. Let its name be U. In the adjacent figure a,b,c,d are names of points. Points a,c are in U, and points b,d is not in U.
Usually all objects involved in a discussion form a collection called a universe. Objects outside a universe are ignored. Aninterior of a rectangle may serve as an example of a universe. Let its name be U. In the adjacent figure a,b,c,d are names of points. Points a,c are in U, and points b,d is not in U. (Geometric) Example 3: In the adjacent figure the universe consists of all points inside and on the rectangle. The interior of the circle together with the circle itself is a subset of the universe. If c is the center then the subset consists of all the points whose distance from c is < the radius of the circle.
(Geometric) Example 3: In the adjacent figure the universe consists of all points inside and on the rectangle. The interior of the circle together with the circle itself is a subset of the universe. If c is the center then the subset consists of all the points whose distance from c is < the radius of the circle.
 In the following sections there are discussions involving more than one open statement, all with the same universe. Two open statements will assign two truth values to each object and determine two subsets (truth sets) in that universe, three open statements - three truth values to each object and three subsets (truth seets) in that universe, etc. The assignments of truth values to objects are done independently. Sometimes colors will be used to coordinate names, open sets and geometric models. The adjacent figure is the geometric model of the truth sets S1, S2 of two unspecified open statements p(x), q(x) . Depending on the positions of the circles, these open statements may assign any of the following pairs of truth values to each object in the universe:
In the following sections there are discussions involving more than one open statement, all with the same universe. Two open statements will assign two truth values to each object and determine two subsets (truth sets) in that universe, three open statements - three truth values to each object and three subsets (truth seets) in that universe, etc. The assignments of truth values to objects are done independently. Sometimes colors will be used to coordinate names, open sets and geometric models. The adjacent figure is the geometric model of the truth sets S1, S2 of two unspecified open statements p(x), q(x) . Depending on the positions of the circles, these open statements may assign any of the following pairs of truth values to each object in the universe:
 The adjacent figure shows the truth sets of two unrelated open sets. The trivial open statements involving point x
The adjacent figure shows the truth sets of two unrelated open sets. The trivial open statements involving point x
 Let S be any set in a universe U. Collect all objects in U but outside of S to form a new set ~S. In the adjacent figure, if S is the set of all points in the left part of the figure, then ~S is the set of all points in the right part.
Let S be any set in a universe U. Collect all objects in U but outside of S to form a new set ~S. In the adjacent figure, if S is the set of all points in the left part of the figure, then ~S is the set of all points in the right part.

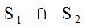

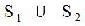
 Occasionally useful is a type of subtraction of sets. Intuitively speaking, the subtraction of a second set set from a first set removes some of the objects in the first set.
Occasionally useful is a type of subtraction of sets. Intuitively speaking, the subtraction of a second set set from a first set removes some of the objects in the first set.


 A restriction on families of sets is: No family can be a set in that family. There are more restrictions but families in discussions here will be simple enough not to violate any of the rules. And in discussions here most sets in a family will be in a common university. The adjacent figure shows a random collection of circles whose interiors form a family.
A restriction on families of sets is: No family can be a set in that family. There are more restrictions but families in discussions here will be simple enough not to violate any of the rules. And in discussions here most sets in a family will be in a common university. The adjacent figure shows a random collection of circles whose interiors form a family.
 [a] The intersection S1 /\ S2 /\ ... /\ Sn consists of all objects in that are in every subset (*).
[a] The intersection S1 /\ S2 /\ ... /\ Sn consists of all objects in that are in every subset (*). [b] The union S1 \/ S2 \/ ... \/ Sn consists of all objects in that are in one or more subsets (*).
[b] The union S1 \/ S2 \/ ... \/ Sn consists of all objects in that are in one or more subsets (*). [c] A family of sets covers a given set if and only if the given set is included in the union of all sets in the family.
[c] A family of sets covers a given set if and only if the given set is included in the union of all sets in the family. [d] A family of sets is disjoint if and only every pair of sets in the family is disjoint.
[d] A family of sets is disjoint if and only every pair of sets in the family is disjoint. [e] A family of subsets of a given set is a partition of a given set if and only if the family is disjoint and covers the given set.
[e] A family of subsets of a given set is a partition of a given set if and only if the family is disjoint and covers the given set.
 [f] A family of sets is an increasing chain of sets if each set is included in the next set (except for the last set).
[f] A family of sets is an increasing chain of sets if each set is included in the next set (except for the last set).